0 引言
在铡草机作业自动或智能控制中,数学模型对作业效率及能耗有重要影响,国内外学者对其建模方法进行了研究[1-6]。BARUAH等[7]以总体能耗来搭建收获机数学模型;JIM[8]以发动机负荷变化建立作业负荷模型,实时调整收获机行走速度;KOTYK等[9]设计农机传输带作物流量模型,实现了收获机作业负荷控制。张认成等[10]基于收获机变质量工况建立模型,实施了作业负荷智能控制;为提升非常负荷的控制精度,姬江涛等[11]建立了收获机脱粒滚筒的最优转速和最优脱粒间隙模型,提高了因作物含水率大等造成堵塞的预测调整可信度和准确性;倪军等[12]以收获机作业时间常数建立模型,利用FPGA设计收获速度控制器;秦云[13]则采用收获机总体作业负荷建立模型,适应不同工况下控制参数输出。上述研究均直接以不同作业参数建立和优化模型,通过以创建其他参数检测条件对所建模型优化及验证的研究鲜有报道。
切碎作物喂入矢角直接影响切碎辊转矩负荷及切碎效能。本文设计液体悬位滚轮式传动带顶压机构,基于SPSS、Matlab对切碎传动带检测压力进行回归分析,建立切碎传动带压力与切碎喂入矢角数学模型,利用检测切碎传动带压力的方法优化及验证切碎作物喂入矢角数学模型。
1 铡草机切碎喂入矢角模型
1.1 切碎装置构成
该铡草机主要包括液压喂入输送机构、作物滚筒切碎器、压扁机构、作物抛送机构、柴油发动机及动力传动机构等部分。铡草主要工作单元位置及切碎作业单元如图1所示[14-15]。

图1 主要工作单元位置及切碎作业单元结构示意图
Fig.1 Main unit of work location and chopping unit diagram
1.抛送装置 2.压扁辊 3.切碎滚筒 4.定刀 5.上喂入辊 6.下喂入辊 7.切碎底弧板
图2为切碎滚筒结构示意图,图中θ1为辊(叶片)轴心至喂入点矢径的水平夹角(作物喂入矢角)、θ2为喂入处输送槽底延长线的水平夹角,是影响作物切碎性能的重要参数。

图2 切碎滚筒结构示意图
Fig.2 Shredding drum
1.切碎滚筒 2.切碎刀具 3.水平轴线 4.切碎作物喂入矢径 5.切碎作物喂入矢角 6.传动带水平角 7.水平线 8.作物传送带 9.待切碎作物
如图3所示,柴油发动机为作物收获提供全部作业所需的基本动力,通过传动机构将动力分配给各作业单元。作业过程中,传动系统通过液压管路系统将部分动力传递给作物喂入辊,传输带托运作物,进给切碎加工,通过传动带将部分动力传递给切碎、压扁、抛送等作业单元。收获机采用HST实现作物喂入速度调节。传动带联动作业系统中切碎辊、压扁辊和抛送风机。
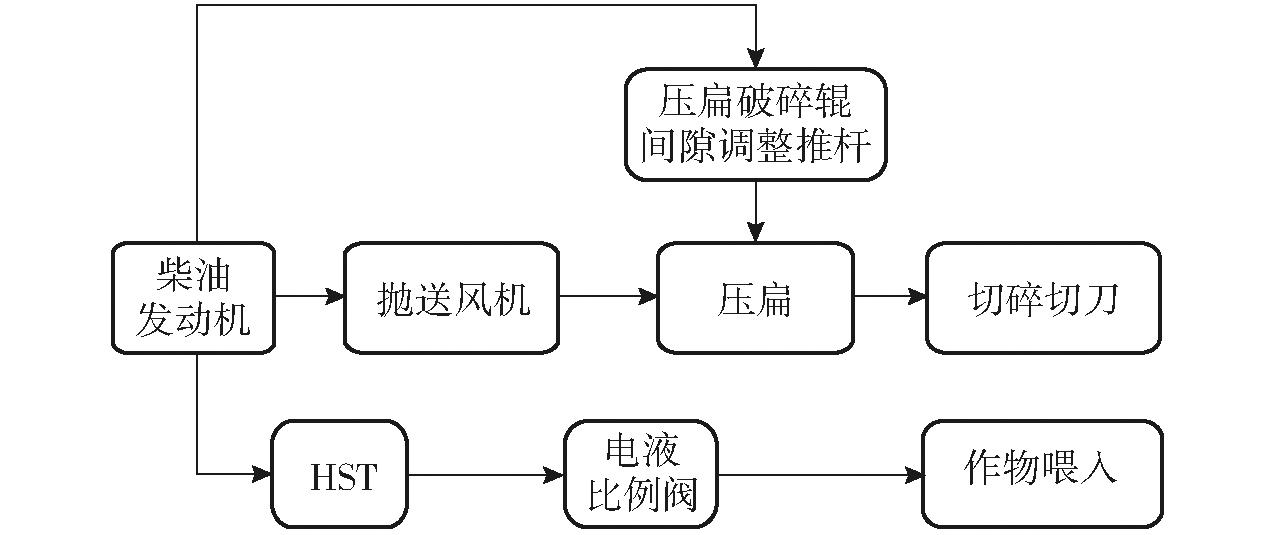
图3 铡草机动力传动系统示意图
Fig.3 Hay cutter power transmission system diagram
饲草作物茎秆通过传输带及喂入辊送入切碎系统进行茎秆切碎加工,而后进入压扁单元进行二次加工,最后由抛送风机将加工完毕的饲草料抛出。
1.2 切碎作物喂入矢角模型建立
1.2.1 作物切碎运动学分析
假设正常切碎过程中,作物连续均匀喂入;作物紧贴盖板与凹板作定常连续流动,作物间相对滑动可忽略;凹板抛出切碎作物速度等于切碎滚筒圆周速度;切碎、压扁、抛送空间均等效为单输入单输出系统,单位长度作物喂入量ρ,已加工与未加工作物质量比Δ。根据切碎、压扁、抛送内各拨齿和作物的运动规律,可得半凹板型径流作物运动数学模型为[13,16-17]
![]()
k1krRω2+g(cosθ-fcsinφsinθ)
(θ∈[2nπ,(2n+1)π]; n∈N)
(1)
其中

式中 r、θ、z——切碎、压扁、抛送空间中作物质点柱面坐标(图4)
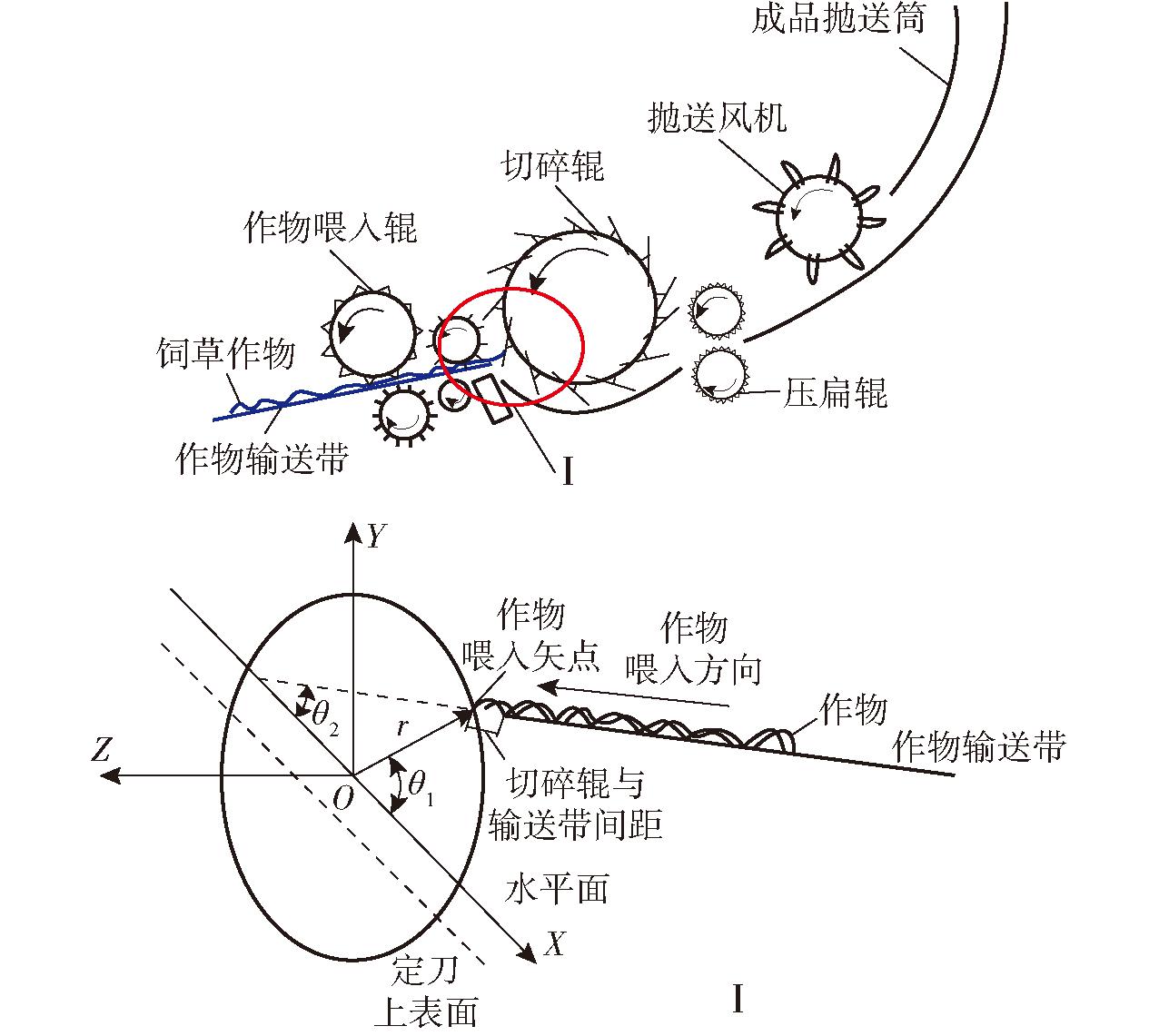
图4 作业空间中作物质点柱面图
Fig.4 Cylinder diagram of crop particle in working space
R——辊(叶片)拨齿作用半径,m
g——重力加速度,m/s2
k1、kr——与辊(叶片)几何参数相关的常数
fc——作物与凹板间摩擦因数
fb——作物与拨齿摩擦因数
δ*——拨齿对作物作用角,rad
φ——作物沿凹板运行螺旋角,rad
μ(z)——沿Z轴方向已加工与未加工作物分离率
e′——速度增长系数 d1——拨齿直径,m
N1——拨齿头数 N2——拨齿列数
L1——辊(叶片)拨齿螺旋节距,mm
ω——角速度
对于作物切向喂入,则式(1)需满足[17]

(2)
式中 vρ——入口处作物速度,kg/s
作物喂入输送槽与切碎辊存在间隔距离,作物须通过此段距离被切割,作物由输送槽到达切碎辊时,θ1、θ2会因切碎辊转速与作物输送速度的变化而改变,设定θ2不变,根据单位时间内作物产品输出量(生产效率),可确定切碎辊转速及作物喂入点位置。
传动带离心力模型为
(3)
式中 α′——带轮包角,rad
C*——传动带离心力,N
q——传动带单位质量,kg/m
v——传动带线速度,m/s
Δα——带轮包角变化量,rad
滚轮顶(压)力与检测机构液体压力传递损失与传动带离心力相抵,离心力随转速的升高而增大。
1.2.2 切碎矢角准确模型构建
切碎过程中,由于切碎装置空间配置关系与切碎数学模型相关度极高,由式(1)可知,作物喂入矢角对切碎辊转速、转矩有影响。切碎辊转矩与作物喂入量存在直接关系。而切碎辊转矩、转速与传动带有效拉力相关,所以,作物喂入矢角与传动带有效拉力(切碎辊圆周力)相关。传动带预压力一般设计约为其应承受有效拉力的1/10,作物喂入矢角与传动带压力存在着关系。为便于跟踪检测,经分析取作物喂入量、切碎辊转速及切碎传动带初始压力3个参数,利用回归分析法对铡草机切碎辊作物喂入矢角模型进行优化,构建作物喂入矢角准确数学模型为
![]()
![]()
(θ∈[2nπ,(2n+1)π];n∈N)
(4)
即
![]() =10xF
=10xF
(5)
式中 F——传动带压力,N
Mrw——传动带力矩,N·m
式(5)中的x通过回归试验求取后,需对切碎矢角初始值进行调整。
1.2.3 切碎辊作物喂入初始矢角调整方法
以铡草机切碎作业单元为研究对象,对切碎传动带实施顶压并进行压力负荷检测,施以最优效能控制约束,在不变载荷下降低切碎作业系统负荷,减少能耗及堵转率,最终提高生产效率。由此,提出通过计算传动带顶压位置及初始顶压力,优化切碎数学模型,从而实现对切碎作业负荷优化控制的目标。
设计了液体悬位顶压滚轮,传动带对液体悬位顶压滚轮施以离心力,离心力被连接于滚轮下方小油缸塞杆,经油缸及与之相连油管内的油液向远端传递,从而连接于液压管路上的压力传感器,信号实现了离心力(传动带压力)接收、标定和发送。如图5a所示, 利用液体压力传递时的不可压缩性,保证了压力传递效率且可部分消化吸收震动能量。液压管路上合理设置流量和初始调压开关(图5b),利用液体压力传递原理,液体不可压缩性与流动性,保证了压力传递效率和可部分消化吸收震动能量。此外,液体悬位顶压滚轮由3套以滚轮托板中心为圆心圆周均布的滚珠导套、导柱支撑,沿Y轴可自由上、下滑动,较好地限制了滚轮X轴、Z轴方向的位移。图5c为切碎传动带压力检测装置实体。
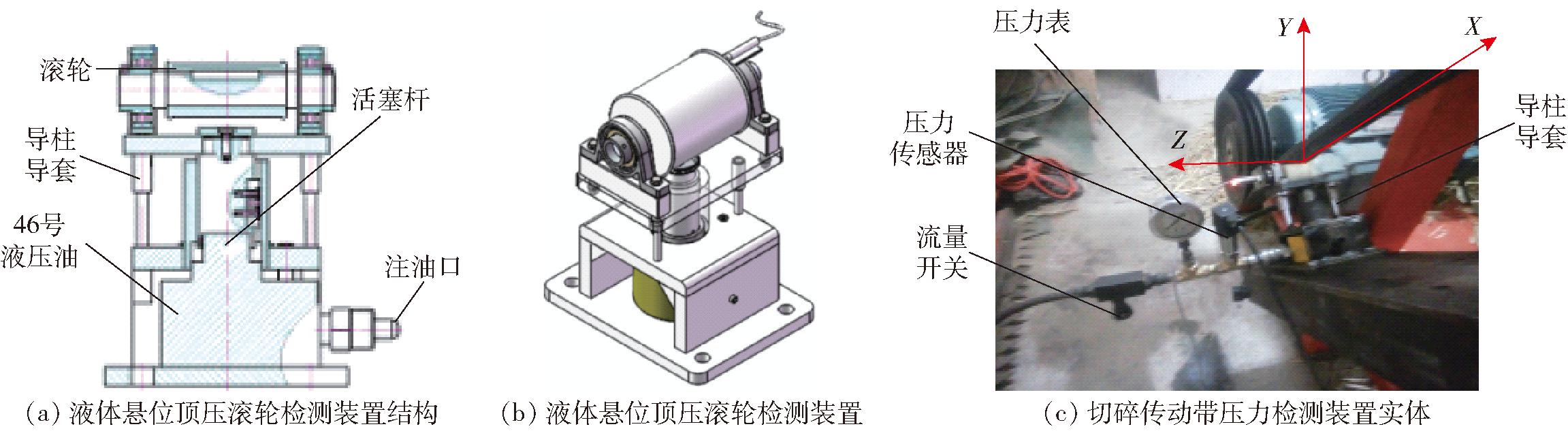
图5 基于传动带压力检测的铡草机切碎负荷检测装置
Fig.5 Cutting load detection device of hay cutter based on transmission belt pressure detection
根据传动带最大圆周力与带轮包角的关系式,采取检测装置沿传动带长度方向安装位置可调,为不削弱和加强底座刚性、强度,作业过程减小抖颤,对检测装置底板进行了改进设计,如图6所示。
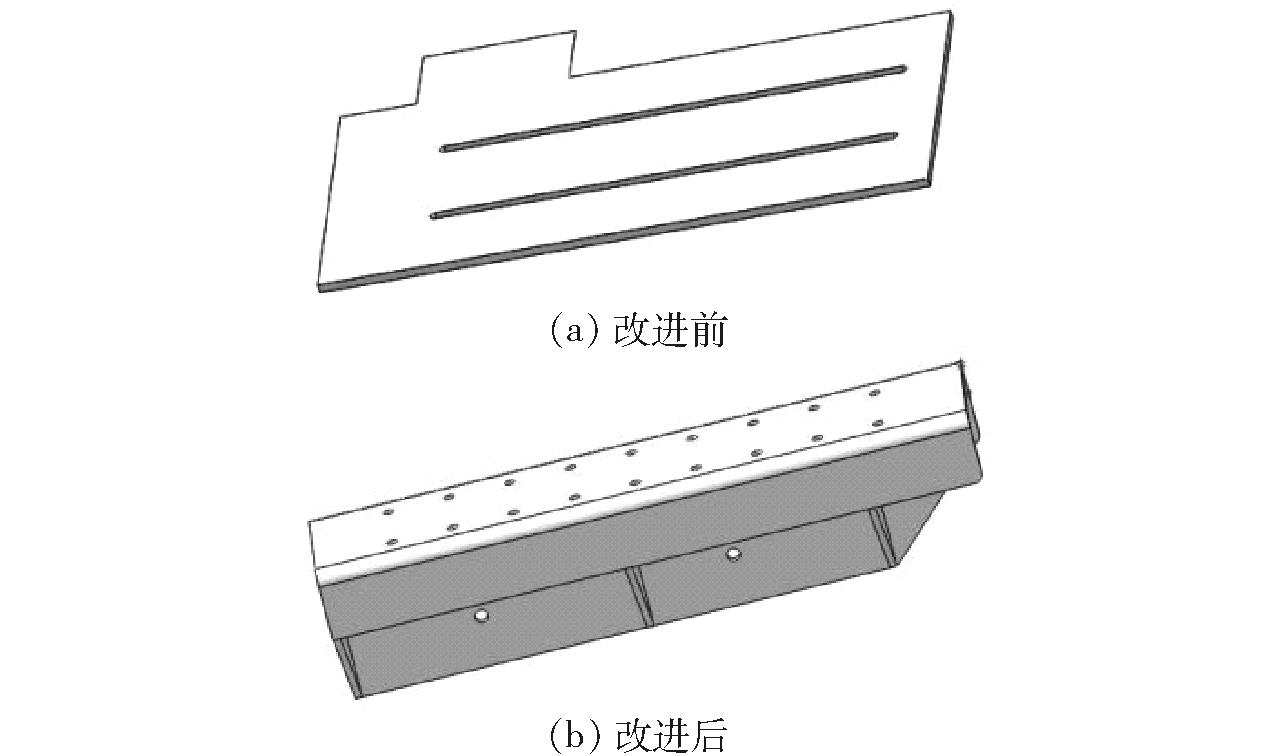
图6 液体悬位顶压滚轮检测装置可调节底座
Fig.6 Liquid suspension top pressure roller detection device adjustable base
图7为切碎辊传动机构带、带轮(大带轮为主动轮,小带轮为从动轮)传动及滚轮顶压的受力情况。图8为带传动滑动率与效率曲线[18]。
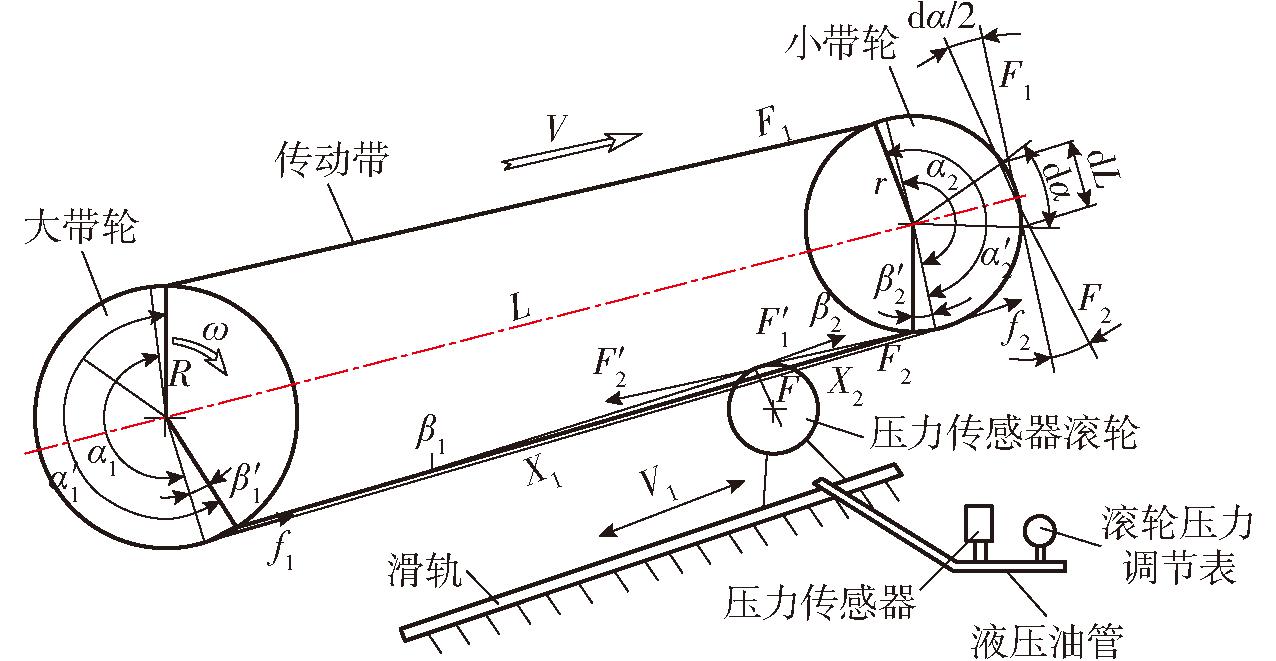
图7 带轮与液体悬位滚轮受力分析
Fig.7 Force analysis diagram of pulley and liquid suspension roller
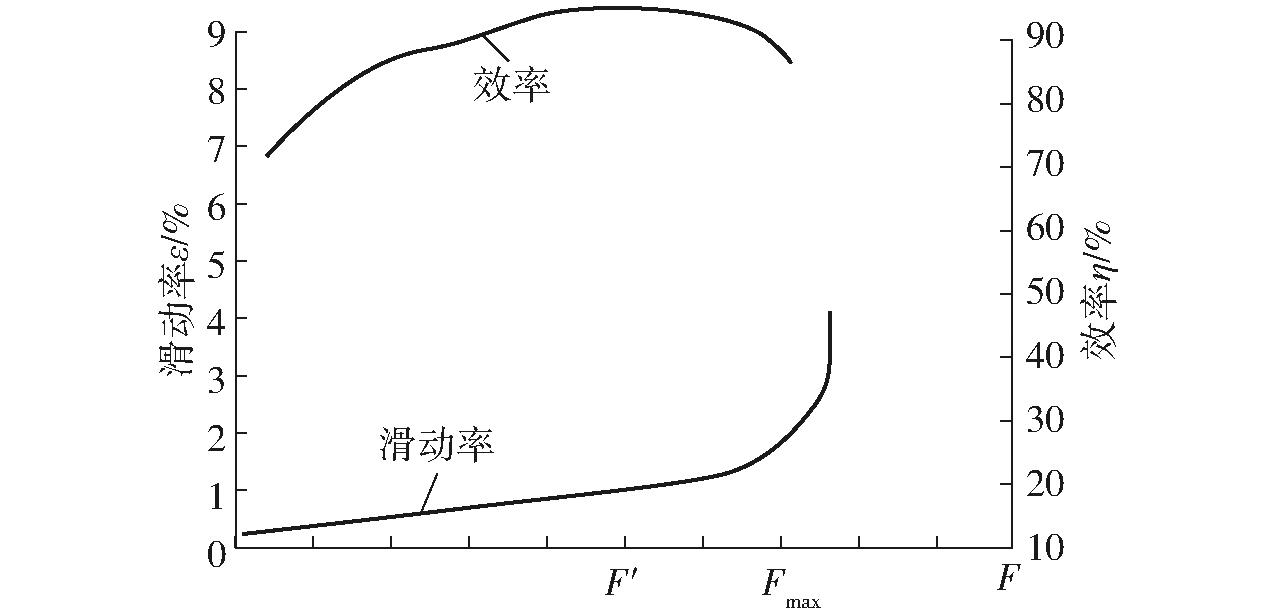
图8 带传动滑动率与效率曲线
Fig.8 Slip curve and efficiency curve of belt transmission
由图7可知,传动带压力液体悬位滚轮检测顶压位置为

(6)
式中 x1——滚轮顶点与大带轮传动带输入点初始距离,mm
x2——滚轮顶点与小带轮传动带输出点初始距离,mm
h——传感器初始压力下传动带相对被顶起高度,mm
α1——大带轮初始包角,rad
α2——小带轮初始包角,rad
β1——大带轮侧传动带顶起角度,rad
β2——小带轮侧传动带顶起角度,rad
R1——大带轮半径,mm
r1——小带轮半径,mm
L——大、小带轮圆心距,mm
E——传动带弹性模量,MPa
A——传动带横截面积,m2
由图7可知,检测装置安装位置应倾向于小带轮绕出点侧。该检测系统下,当主轴作业额定转速及负载增大,传动带液体悬位顶压滚轮初始值及滚轮顶起传动带初始高度(p0,h)均应靠近下限取值,这与传动带有效拉力确定时,根据材料物性、几何尺寸等适当减小力传递系数,可保证传动带较低滑动率与较高生产效率相一致。
图9为模型优化前后作业负荷控制轨迹。由图9可得, 同一作物喂入量工况下,优化模型切碎作业负荷较小。
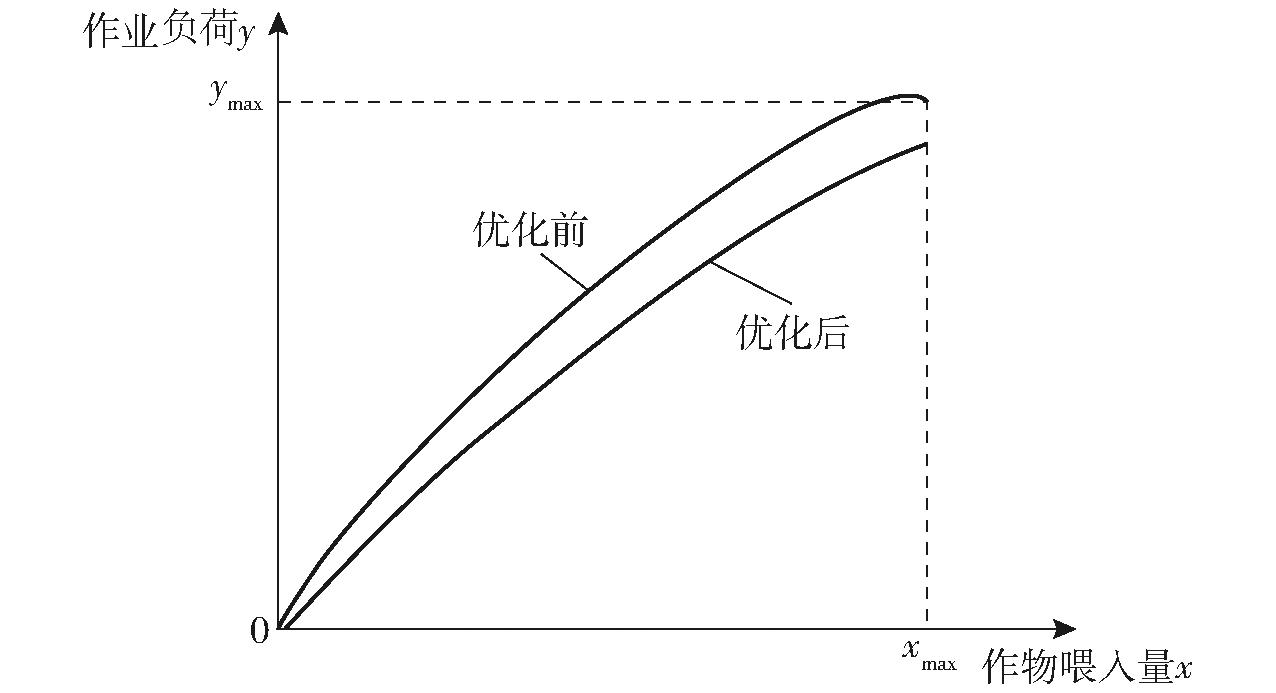
图9 模型优化前后作业负荷控制轨迹示意图
Fig.9 Schematic of workload control trajectory before and after detection optimization
如图10a、10b所示,压力传感器由其尾端管螺纹,将腔体与液压管路连接相通,液压站向液压管路排液施压,当传感器腔体内的膜片接收到腔体内液体压力时,通过机械受力关系,将被测压力传递给腔体内的压电元件,最后由压电元件输出,与被测压力成一定关系的电信号。图10c描述了检测系统液压工作回路,利用液压、带传动理论,设计液体介质式传动带压力检测系统,基于检测系统搭建整机最优效能作业模型,确定压力检测时传动带顶压位置,计算传动带压力初始值的设置范围,建立传动带压力检测理论指标模型与各种工况回归模型。
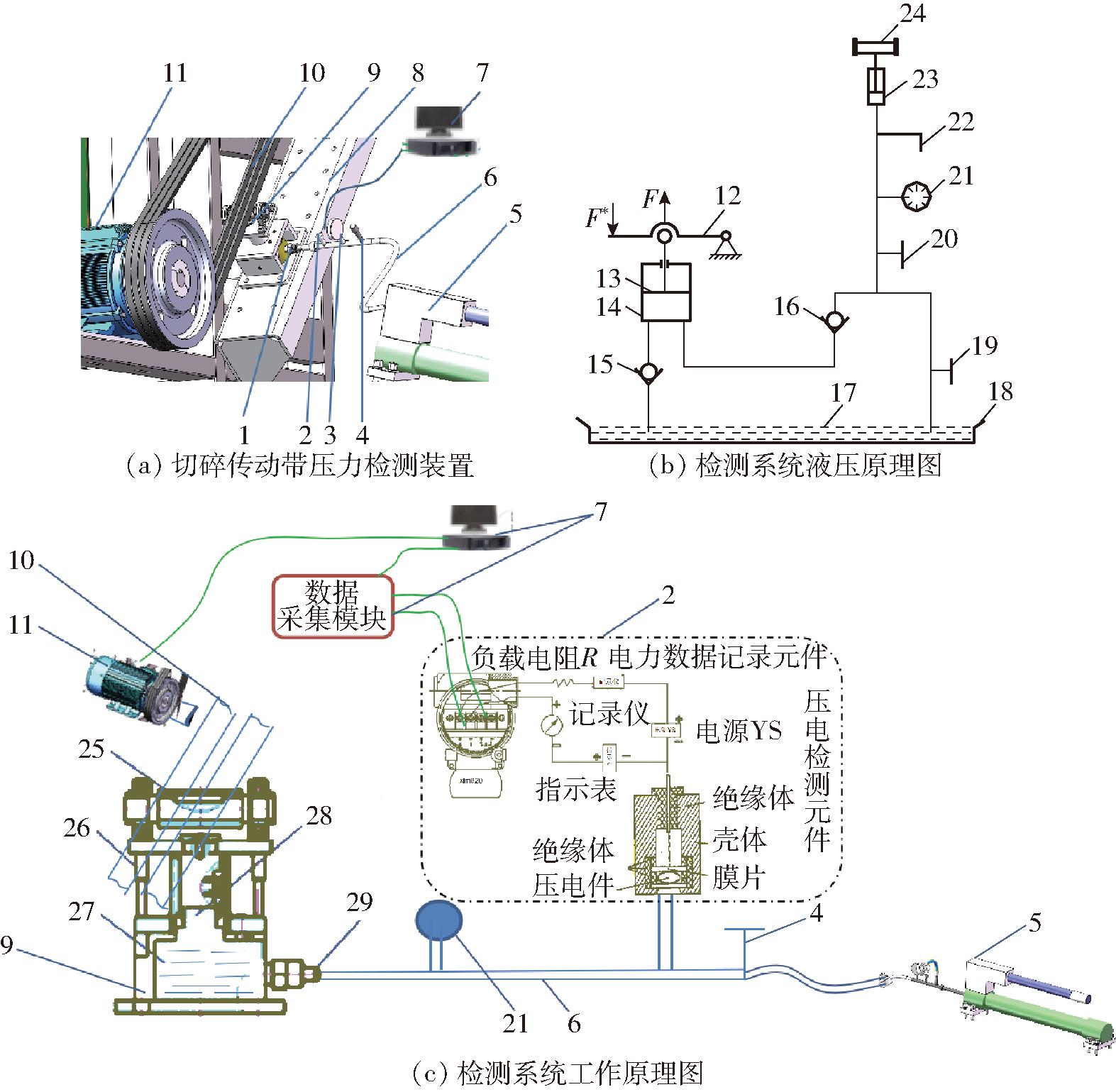
图10 切碎传动带压力液压式检测工作原理图
Fig.10 Working principle diagrams of hydraulic pressure detection for shredded transmission belt
1.活塞杆油缸 2、22.压力传感器 3、21.压力表 4.流量与初始调压开关 5.液压站 6.液压油管 7.压力测控系统 8.调节底座 9.传动带液体悬位顶压滚轮 10.传动带 11.发(电)动机 12.杠杆手柄 13.小活塞 14.小缸体 15、16.单向阀 17.液压油 18.油箱 19、20.截止阀 23.活塞 24.顶压滚轮 25.滚轮 26.导柱导套 27.46号液压油 28.活塞杆 29.注油口
经液压油管向液体悬位滚轮底座油腔内注油加压,使滚轮顶起(可沿滑轨调整位置)传动带一定高度,压力传感器则可立刻采集到传动带压力。实现对传动带压力负荷检测需满足条件[19]
(7)
式中 p0——传感器设定初始压力,MPa
Δp0——喂入载荷后传感器压力变化量,MPa
p*——传感器量程,MPa
λ——沿程阻力系数
ξ——局部阻力系数
v1——液体下游流速,m/s
d——管直径,mm l——管长度,mm
μ——液体动力粘度,Pa·s
检测系统内的油液量决定液体悬位顶压滚轮初始压力上限值。通过对活塞杆油腔形状及油液量计算设置,可凭借滚轮位移势能变化、液体流动生热散失等部分吸收外来多余的冲击震动能量,起到减小传动带震动、提升负荷数据检测质量及最大作业能力作用。
2 仿真与回归分析
借助SPSS、Matlab软件,对以下各工况(试验过程中天气晴,环境温度30℃)的传动带压力负荷数据,进行回归显著性及响应面分析[20-22]。
2.1 试验参数
确定对试验台负荷检测系统工作性能影响较为显著的因素为:作物单位长度喂入量(检测位置)、切碎辊转速(喂入载荷后传感器压力变化量Δp0)、传动带初始压力(传感器设定初始压力p0)。试验时选取切碎辊转速分别为800、1 200、1 600 r/min;传动带初始压力分别为0.6、1.2、1.8 MPa。
浮动辊与固定辊之间转速差为20%,喂入物料选取切碎间隙为1.0 mm。根据青贮机田间实际作业工况,喂入量与作业速度关系式为[23]
ρ=BMv2/10 000
(8)
式中 ρ——作物单位长度喂入量,kg/s
B——割幅,m
M——作物产量,kg/hm2
v2——机组行驶速度,m/s
切碎辊有效工作长度为0.4 m,在不同作业速度时,作物单位长度喂入量分别为1.5、3.5、5.5 kg/s。
2.2 试验设计
同时保证作业质量及效率目标下,作物喂入量、传动带初始压力、传动带转速作为3个试验因素,以传动带压力最大检测偏差、准确率(AUC)为指标,建立回归模型。试验因素与水平如表1所示。
表1 试验因素与水平
Tab.1 Experimental factors and levels
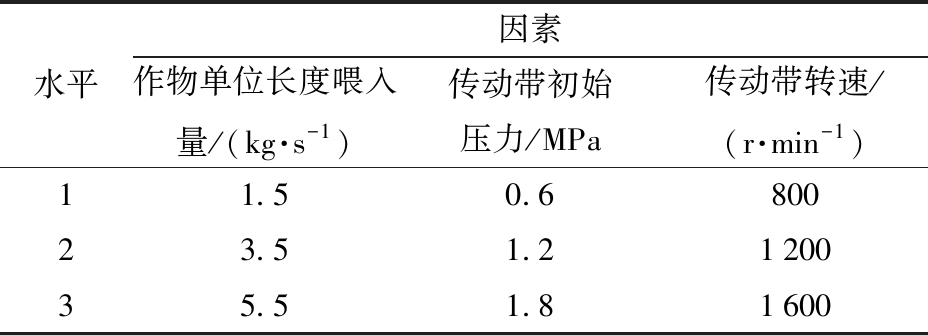
水平因素作物单位长度喂入量/(kg·s-1)传动带初始压力/MPa传动带转速/(r·min-1)11.50.680023.51.2120035.51.81600
2.3 回归模型建立与显著性分析
试验方案及结果如表2所示,表中A、B、C为水平值。
表2 试验方案及结果
Tab.2 Test scheme and results

试验序号作物单位长度喂入量A传动带初始压力B传动带转速C传动带压力最大检测偏差/MPa传动带压力检测准确率/%12110.13683.1021221.75473.1733330.73869.6042120.63652.3452130.69849.5762310.84361.8873330.70570.8383210.64973.1591110.18656.91传动带压力最大检测偏差K111.4772.1411.477K122.1772.5393.101K132.5891.7671.060R11.1120.7722.041因素主次C、A、B最优组合A3B2C2传动带压力检测准确率K21206.27190.00206.27K22163.79229.42195.89K23203.23188.39209.61R242.4841.0313.72因素主次A、B、C最优组合A1B2C3
由表2可知,检测偏差最优组合为A3B2C2,即作物单位长度喂入量5.5 kg/s、传动带初始压力1.20 MPa、传动带转速1 200 r/min;检测准确率最优组合为A1B2C3,即作物单位长度喂入量1.5 kg/s、传动带初始压力1.20 MPa、传动带转速1 600 r/min。
检测质量指标方差分析结果见表3。由表3可知,对于传动带压力检测偏差指标,在置信度95%下,传动带初始压力影响显著,作物单位长度喂入量与传动带转速影响不显著。对于检测准确率,在置信度95%下,作物单位长度喂入量、传动带初始压力及传动带转速影响均显著。
表3 传动带压力数据检测质量指标方差分析
Tab.3 Variance analysis of planting seedling quality indexes

注:*表示显著(0.01≤P≤0.05)。
指标方差来源离差平方和自由度平均离差平方和FP作物单位长度喂入量0.00110.0012.2960.370传动带压力最大传动带初始压力0.25010.250458.9980.030∗检测偏差传动带转速0.19020.095174.3760.053误差0.00110.001作物单位长度喂入量342.9581342.958453.3780.030∗传动带压力检测传动带初始压力225.1441225.144297.6330.037∗准确率传动带转速692.7042346.352457.8650.033∗误差0.75610.756
2.4 试验因素对性能指标的影响
各因素对传动带压力检测偏差的响应曲面如图11所示。
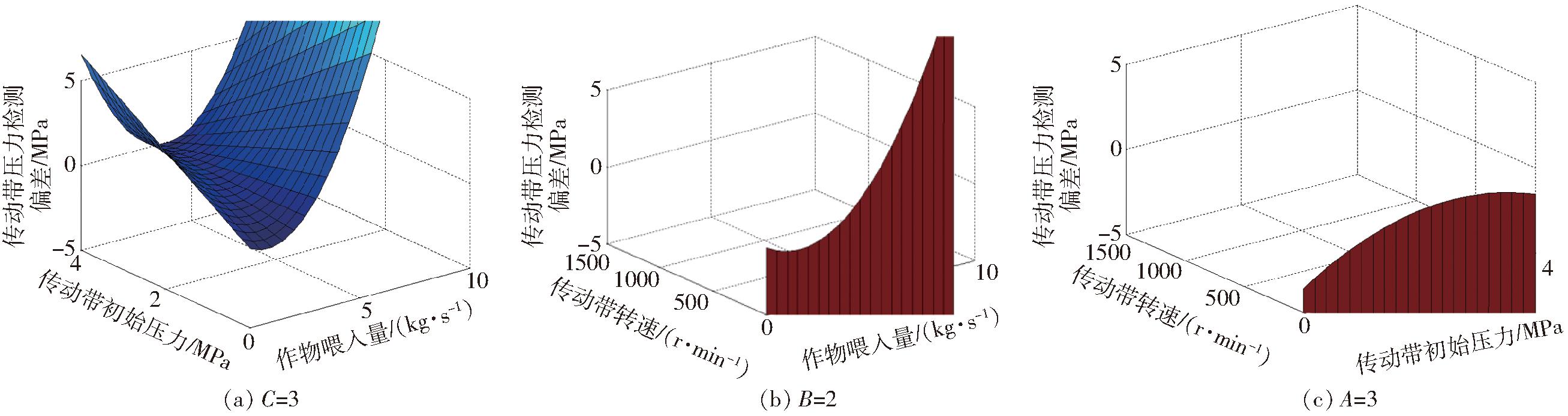
图11 试验因素对压力检测偏差的影响
Fig.11 Effects of test factors on pressure deviation
由图11a可知,传动带压力检测偏差随着作物喂入量和传动带初始压力的增大而增大,但前者增
幅更大,可见作物喂入量加大使传动带发生了较大的震颤。由图11b可知,传动带初始压力一定时,传动带压力检测偏差均随着喂入量的增大,先减小后增大,检测装置减震效果趋于弱化。由图11c可知,当作物喂入量一定时,传动带压力检测偏差随着传动带初始压力的增大而增大,但增大到一定数值后趋于不变,可见传动带因张紧度增大而减小了传动带振动。
各因素对传动带压力检测准确率响应曲面如图12所示。
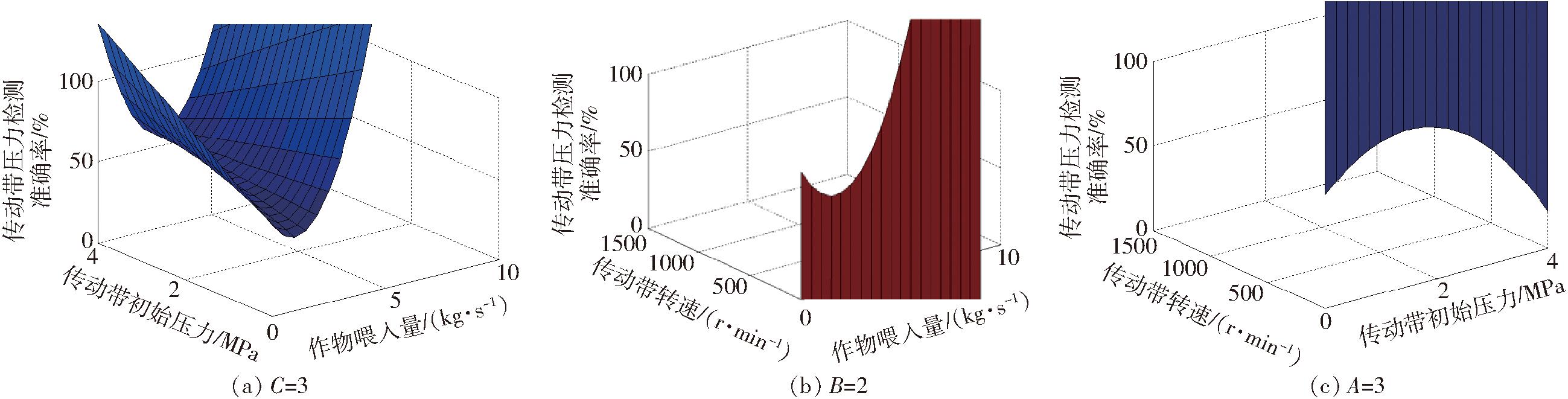
图12 试验因素对压力检测准确率的影响
Fig.12 Effect of experimental factors on pressure accuracy
由图12a可知,传动带压力检测准确率的变化趋势近似于图11a,不同的是传动带初始压力对检测准确率影响更小,因传动带初始压力与传动带压力呈一次关系。由图12b可知,传动带初始压力一定时,传动带压力检测准确率随着作物喂入量增加,先减小后增大,检测装置减震弱化,但始终有效。由图12c可知,作物喂入量一定时,传动带压力检测准确率随着传动带初始压力增大,呈先增大后减小的趋势,可见,在给定作业速度下,作物喂入量与传动带初始压力均存在一组数值,能够使传动带压力检测准确率最优。
2.5 试验因素影响效应
贡献率K反映单个因素对所建立回归模型的影响,K越大,影响程度就越大,K计算式为
(9)
其中
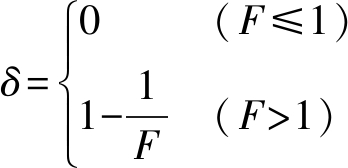
(10)
式中,方差分析值F为考核值。根据式(9)、(10)计算出作物喂入量、传动带初始压力及传动带转速对目标值的贡献率K,作物喂入量、传动带初始压力及传动带转速对检测偏差贡献率分别为0.482、1.425、0.837,对检测准确率目标值的贡献率分别为0.365、0、0.438。
传动带初始压力对传动带压力负荷的影响最大,作物喂入量影响最小。传动带转速对传动带负荷检测准确率的影响最大,作物喂入量的影响次之,而传动带初始压力无影响。可见,传动带初始压力仅影响模型最大检测偏差,而与模型准确率无关。
2.6 最佳参数组合确定
通过上述试验分析可知,作物喂入量、传动带初始压力、传动带转速等影响因素对传动带压力检测最大偏差和准确率2个指标影响程度各不相同,为分析各因素对整机负荷检测质量综合影响效果,应用模糊综合评价法对正交试验结果进行综合优化,找出最佳参数组合。首先分别建立2个指标隶属度模型,得出各指标每次试验的隶属度见表4。由隶属度构成模糊关系矩阵R为[24]
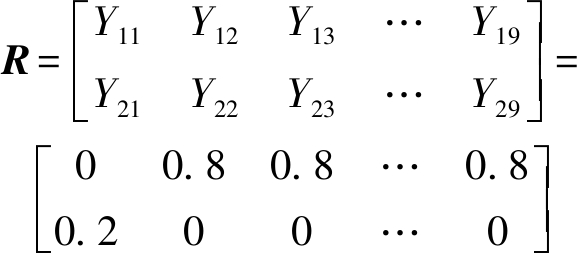
(11)
表4 综合评分结果
Tab.4 Results of comprehensive evaluation
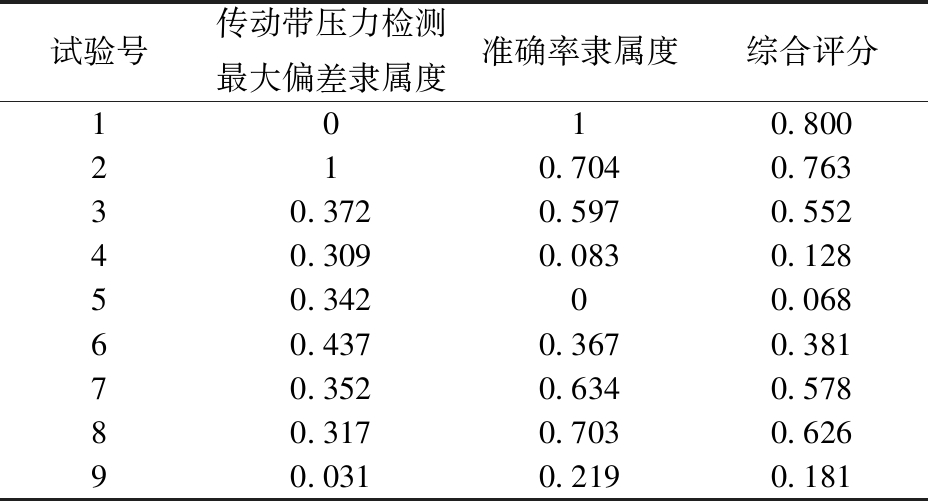
试验号传动带压力检测最大偏差隶属度准确率隶属度综合评分1010.800210.7040.76330.3720.5970.55240.3090.0830.12850.34200.06860.4370.3670.38170.3520.6340.57880.3170.7030.62690.0310.2190.181
其中
式中 Yin——指标Xi的第n次试验获得的隶属度
Ximax——指标Xi最大值
Ximin——指标Xi最小值
Xin——指标Xi的第n次试验获得的隶属度
根据传动带压力负荷检测2个性能指标的重要性,确定权重分配集为0.2、0.8,即传动带压力检测最大偏差和准确率权重分别为0.2、0.8。由模糊矩阵R与权重分配集P确定模糊综合评价指标W,其中W=PR,综合评分结果见表4,最后将综合评分结果进行极差分析见表5,分析结果表明,综合影响检测精度指标的主次因素为A、B、C,最优组合为A3B2C3,即作物单位长度喂入量5.5 kg/s、传动带初始压力1.20 MPa、传动带转速1 600 r/min。综合评分方差分析见表6,结果表明:在置信度95%下,传动带初始压力、传动带转速对传动带压力检测影响显著,作物单位长度喂入量影响不显著,检测准确率得到提高。
表5 综合评分极差分析
Tab.5 Range analysis of comprehensive evaluation
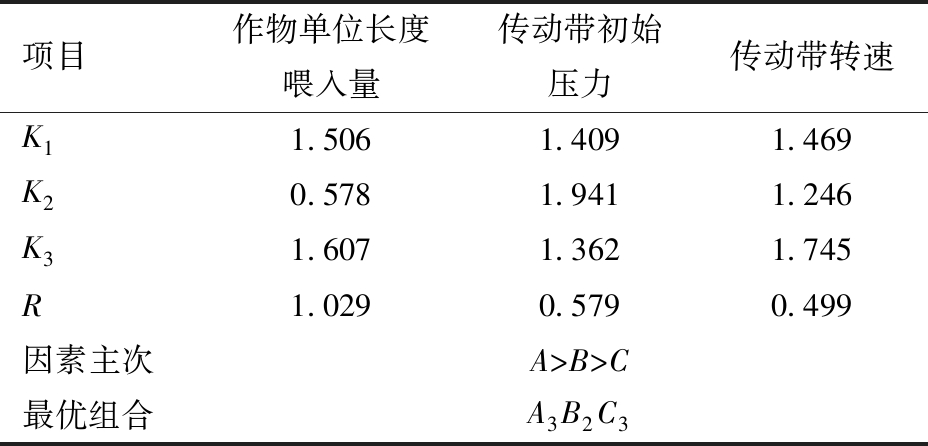
项目作物单位长度喂入量传动带初始压力传动带转速K11.5061.4091.469K20.5781.9411.246K31.6071.3621.745R1.0290.5790.499因素主次A>B>C最优组合A3B2C3
表6 综合评分方差分析
Tab.6 Variance analysis of comprehensive evaluation
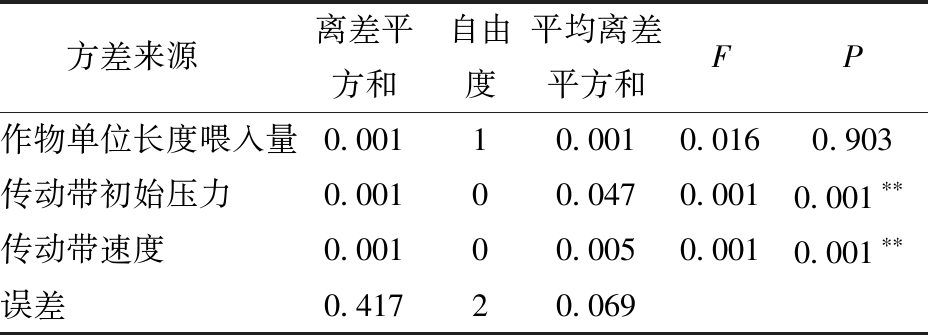
注:**表示极显著(P<0.01)。
方差来源离差平方和自由度平均离差平方和FP作物单位长度喂入量0.00110.0010.0160.903传动带初始压力0.00100.0470.0010.001∗∗传动带速度0.00100.0050.0010.001∗∗误差0.41720.069
2.7 矢角模型优化
根据最优(作物喂入量、传动带初始压力、传动带转速)参数组合,由传动带初始压力、传动带转速,计算出![]() 由作物喂入量、传动带初始压力,计算出传动带压力
由作物喂入量、传动带初始压力,计算出传动带压力![]() 与F比较,计算系数,即
与F比较,计算系数,即
![]()
![]()
(θ∈[2nπ,(2n+1)π];n∈N)
经查表计算得:fc=0.2,k1=1.09,kr=26.76,将最优组合参数代入式(1),得
![]() ≈54.08 N
≈54.08 N
(12)
将最优组合参数代入式(3),得
C*≈715.84 N
(13)
最优参数组合下作业时,测得对应切碎传动带压力为 3.5 MPa(343 N)。根据式(5),经式(12)、(13)比较,x1=0.152(离心力近似等于传动带压力时)、x2=0.317,因满足10>10x2>10x1,所以矢角模型取得了明显的优化效果,模型精度提高约2.08倍。优化前、后,矢角θ与传动带压力F的关系分别为

(14)
如图13所示,优化后较优化前切碎传动带压力随切碎喂入角的上升缓慢,同等作物喂入量下,优化模型切碎辊转速更小。

图13 切碎作物喂入初始矢角与传动带压力关系曲线
Fig.13 Relationship between initial vector angle and drive belt pressure
切碎喂入矢角数学模型优化前、后测得切碎传动带压力与切碎喂入矢角理论模型计算得传动带检测压力相比较,如图14所示。切碎喂入矢角模型回归方程为
(15)

图14 各切碎喂入矢角数学模型下传动带检测压力对比
Fig.14 Comparison chart lines for each detection mode
由图14可知,随着传动带速度的增大,优化前、后切碎喂入矢角模型精度均趋于提高。由图13、14可知,根据传动带压力与转速的关系以及传动带压力与切碎矢角的关系,对传动带检测压力数据进行数据处理,以此达到建立与应用切碎作物喂入矢角模型式(14)的目的。
2.8 矢角优化模型特性仿真
设定发动机节气门额定位置、HST及流量比例阀传动比不改变,在玉米秸秆单位长度喂入量激励作用下,测试切碎辊稳态工作速度仿真结果如图15所示。

图15 各作业单元开环转速稳态仿真曲线
Fig.15 Steady state simulation curves of open-loop speed for each homework unit
由图15a可知,由于作物单位长度喂入量加大,喂入辊负载力矩增大,喂入辊输出转速下降。由图15b可知,由于作物单位长度喂入量加大,切碎辊负载力矩增大,切碎辊输出转速下降。一开始喂入负荷较小时,切碎转速都呈近似线性下降,当作物喂入量增加到某一临界点时,尤其切碎转速开始呈明显的非线性下降趋势。
HST及比例阀传动比保持额定,试验台在作物单位长度喂入量5.5 kg/s下稳定作业后,15 s时作物喂入量施加阶跃激励2 kg/s,测试切碎辊转速瞬态响应,如图16所示。
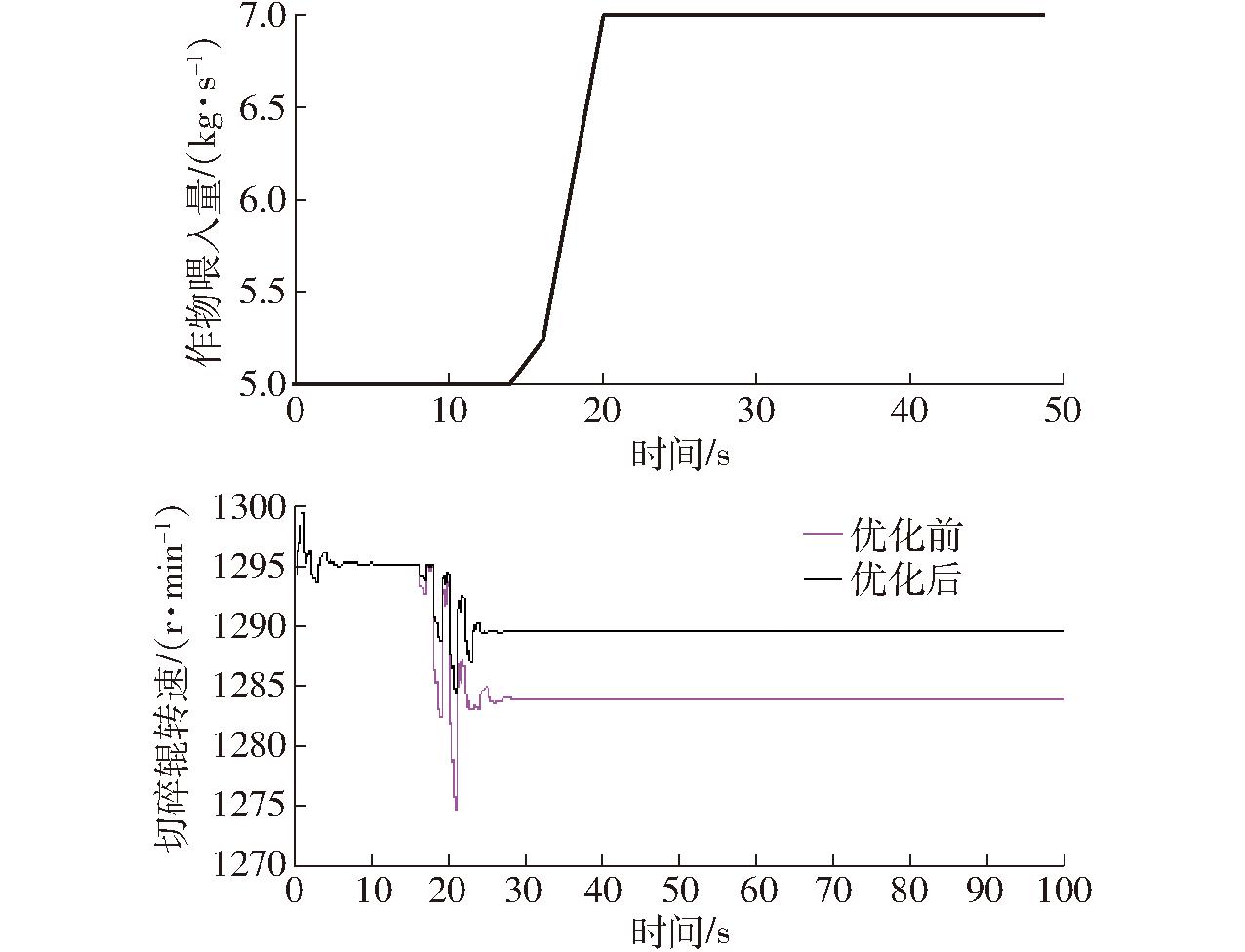
图16 单位长度喂入增量阶跃扰动下的各转速瞬态响应仿真
Fig.16 Simulation of transient response at various speeds under incremental step disturbance of unit length feeding
由图16可知,由于喂入负荷加大,切碎辊负载力矩增大,发动机输出转速下降。随着发动机转速下降,作物喂入量得到一定程度的减小,从而引起切碎辊转速少量恢复性提高。优化前、后,切碎系统对作物喂入量扰动的总时间分别约为2.5、1.8 s,优化切碎数学模型时间常数小、动态响应性好。
3 验证试验
3.1 试验方法设计
铡草机试验台首先在单位长度喂入量2.5 kg/s稳定作业,稳定作业一段时间后,再施加至单位长度喂入量5.5 kg/s,模拟作物密度突变,以测试试验台发动机转速、喂入辊转速、切碎辊转速稳态、瞬态响应情况,并与理论计算、仿真值对照分析,阐述差异原因以及初步给出合理调整措施等。试验步骤:矢角优化模型及优化前模型控制下作物喂入量波动扰动试验。分析稳态、扰动瞬态误差试验值及秸秆切碎质量[25]。
3.2 试验条件与参数设置
如图17所示,该铡草机具有机、电、液俱全,喂入单元和局部整体(切碎、压扁、抛送由传动带刚性连接,本文以切碎为控制研究对象)构成的结构特点,可一次性完成全株作物茎秆、秸秆输送喂入、切碎等多项作业,且数学关系模型具有较强的完整性及典型代表性。该铡草机属中型机型,作业系统采用端部喂入、侧面传动、滚筒式切碎结构。铡草机主要部件及技术参数如表7所示。
表7 铡草机主要部件及作业技术参数
Tab.7 Hay cutter main parts and operation technical parameters

参数数值/型式机体长×宽×高/(mm×mm×mm)5454×2180×4319传动系统型式HST 标准V形传动带喂入系统型式传输带切碎装置结构形式滚筒式滚刀转速/(r·min-1)1300试验作物玉米秸秆(秆径(20±1)mm,含水率5%^15%)喂入方式液压马达输送带自动喂入作物单位长度喂入量/(kg·s-1)5刀辊型式平板形滚筒式切碎器刀辊规格直径×长度/(mm×mm)476×560动刀排列方式 V形排列动刀数量16动、定刀间隙/mm1滑切角/(°)10喂入幅宽/mm400喂入方式并排平铺传动带标准V形生产率/(kg·h-1)1.7×104(新鲜饲草)

图17 铡草机样机
Fig.17 Guillotine prototype
1.抛送装置 2.压扁调制单元 3.发动(电动)机 4.喂入系统 5.切碎单元
为测试测控系统实际运行效果,利用玉米秸秆进行切碎试验,玉米秸秆试验样件制备如图18所示。

图18 玉米秸秆试验样件制备
Fig.18 Sample preparation for corn straw test
3.3 结果分析
选取优化前、后的切碎喂入矢角数学模型进行作业,模型优化前、后玉米秸秆收获效果如图19所示。

图19 玉米秸秆切碎效果
Fig.19 Effects of corn straw chopping
对玉米秸秆进行切碎试验后,依据DB23/T 3636—2023、B15/T 1089—2017等黄贮标准进行测量和统计分析,对优化切碎喂入矢角模型的生产效率及质量指标进行验证,如表8所示。
表8 玉米秸秆切碎试验结果
Tab.8 Results of corn straw chopping test
参数秸秆含水率/%纯工作小时生产率/(kg·h-1)平均切草长度/mm破节率/%标准草长率/%数值8.6±0.011.89×10418.30 ± 5.5095.0 ± 0.5296.70 ± 1.24
由表8可知,优化算法控制下玉米秸秆纯工作小时生产率超过了设计生产率,符合相关标准;实测切草长度Lc为4~20 mm,平均切草长度在设计值(0.7~1.2)Lc范围内,标准草长率达到96.70%,符合国家标准。
切碎优化数学模型检测精度如表9所示。
表9 优化后模型检测精度
Tab.9 Optimized model detection accuracy

参数发动机输入转速/(r·min-1)发动机怠速/(r·min-1)单位长度作物秸秆喂入量/(kg·s-1)传动带压力初始值/MPa传动带压力输入值/MPa检测最优回归值/MPa传动带压力检测最大偏差/MPa传动带压力检测准确率/%数值16008005.501.203.281.9060.49179.52
优化前、后切碎模型对负荷控制能耗如表10所示。
表10 控制模型切碎能耗
Tab.10 Cutting energy consumption of each control model
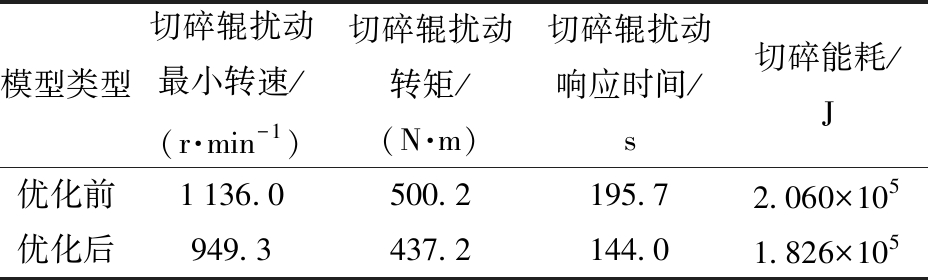
模型类型切碎辊扰动最小转速/(r·min-1)切碎辊扰动转矩/(N·m)切碎辊扰动响应时间/s切碎能耗/J优化前1136.0500.2195.72.060×105优化后949.3437.2144.01.826×105
由表10可知,现场试验与特性结果趋势基本一致,优化的切碎喂入矢角模型下切碎扰动响应时间缩短约26.41%,作业能耗减小约11.36%。
铡草机切碎辊作物喂入矢角模型精度与最大作业效率关系规律为:切碎喂入矢角的变化率与切碎辊传动带压力存在近似线性关系,通过试验可得最优线性系数,由此,切碎作业前,可根据以上规律提前计算设定切碎喂入初始矢角;对于不同工况作业时,可以根据矢角模型计算结果,借助切碎传动带液体悬位顶压装置调节,得到适合切碎喂入初始矢角。
4 结论
(1)通过对作物切碎进行运动学、动力学理论推导,分析饲草作物切碎机理,阐明切碎质量、能耗生成过程及其诱因,借助便于检测的传动带压力参数,建立不便检测但对切碎作业有重大影响的铡草机切碎辊作物喂入矢角数学模型,利用Simuilink对铡草机的稳态特性、扰动瞬态响应进行研究。结果表明,铡草机切碎喂入矢角数学模型对其工作状态有明显的影响。
(2)通过传动带压力液体式悬位滚轮机构的设计应用,得出作物单位长度喂入量5.5 kg/s、传动带初始压力1.20 MPa、切碎辊转速1 600 r/min的参数组合下,可使切碎喂入矢角数学模型最优,模型精度提高2.08倍,切碎系统对作物喂入的扰动时间响应提高约26.41%,切碎能耗降低约11.36%,提高了传动带阻尼减震和传动效率,保证了铡草机切碎模型精度及切碎效能。
(3)设计田间工况对铡草机进行了作物密度扰动的控制试验。试验结果表明,优化切碎喂入矢角数学模型下单位作业能耗明显减少,作业响应性提高,整机作业功效获得提升。
[1] 娄红华.粮改饲的背景及意义[J].现代化农业,2024(4):81-83.LOU Honghua. The background and significance of grain to feed conversion[J].Modernizing Agriculture,2024(4):81-83.(in Chinese)
[2] 李兴霞.基于过采样技术提高农田数据采集精度的研究[J].哈尔滨商业大学学报(自然科学版),2011,27(3):362-364.LI Xingxia. Study on improvement of accuracy of field data collection methods based on oversampling technology[J].Journal of Harbin University of Commerce(Natural Sciences Edition),2011,27(3):362-364.(in Chinese)
[3] 宋占华, 邢书仑, 王征,等. 苜蓿调制试验台测控系统设计与试验[J].农业机械学报, 2021,52(2): 122-134. SONG Zhanhua,XING Shulun,WANG Zheng, et al. Design and experiment of measurement and control system for alfalfa conditioning test bench[J]. Transactions of the Chinese Society for Agricultural Machinery,2021, 52(2): 122-134.(in Chinese)
[4] 刘丽莉.茎穗兼收玉米收获机试验示范探讨和启示[J].农机质量与监督,2022(5):18-19.LIU Lili. Discussion and revelation on experimental demonstration of stem-ear simultaneous harvesting corn harvester[J].Agricultural Machinery Quality &Supervision,2022(5):18-19.(in Chinese)
[5] 崔永杰,王明辉. 农业领域自动定向技术研究进展分析[J].农业机械学报,2023,54(4):1-20.CUI Yongjie, WANG Minghui. Analysis on research progress of automatic orientation technology in agricultural field[J].Transactions of the Chinese Society for Agricultural Machinery, 2023,54(4):1-20.(in Chinese)
[6] 朱光强. 鲜食玉米仿生摘穗机理及装置研究[D].哈尔滨: 东北农业大学,2023.ZHU Guangqiang. Study on mechanism and device of bionic ear picking of fresh maize[D]. Harbin: Northeast Agricultural University,2023.(in Chinese)
[7] BARUAH D C, PANESAR B S. Energy requirement model for a combine harvester, part I: development of component models[J]. Biosystems Engineering, 2005, 90(1): 9-25.
[8] JIM K. Computer controls for the combine[J]. Agricultural Engineering, 1983, 64(2):7-9.
[9] KOTYK W M, KIRK T G, KLASSEN N D, et al.Control system for combine harvesters[C]∥Wescanex 91 IEEE Western Canada Conference on Vomputer.IEEE, 1991.
[10] 张认成, 桑正中. 轴流脱粒滚筒模糊控制仿真[J]. 农业机械学报, 2001, 32(2): 45-48. ZHANG Rencheng, SANG Zhengzhong. Simulation research on the fuzzy logic control of an axial threshing cylinder[J].Transactions of the Chinese Society for Agricultural Machinery, 2001, 32(2):45-48.(in Chinese)
[11] 姬江涛, 王荣先, 符丽君. 联合收获机喂入量灰色预测模糊PID控制[J]. 农业机械学报, 2008, 39(3): 63-66.JI Jiangtao,WANG Rongxian, FU Lijun. Grey prediction fuzzy PID control of the feeding quantity in combine[J].Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(3):63-66.(in Chinese)
[12] 倪军, 毛罕平, 程秀花. 基于FPGA的联合收获机脱粒滚筒模糊控制系统[J]. 农业机械学报, 2009, 40(7): 83-87.NI Jun, MAO Hanping, CHENG Xiuhua. Fuzzy control system of combine cylinder based on FPGA[J].Transactions of the Chinese Society for Agricultural Machinery, 2009,40(7):83-87.(in Chinese)
[13] 秦云.联合收割机负荷控制系统研究[D].镇江:江苏大学, 2012. QIN Yun. Study on load control system of combined harvester[D]. Zhenjiang: Jiangsu University, 2012. (in Chinese)
[14] 张国庆. 全株青贮饲料铡切调质机的研制[D].泰安:山东农业大学, 2020.ZHANG Guoqing. Development of whole plant silage cutting and conditioning machine[D].Taian: Shandong Agricultural University, 2020.(in Chinese)
[15] 王征,任龙龙,李扬,等.扰动下铡草机切碎辊负荷控制器设计与试验[J].农业机械学报, 2023,54(12):141-154.WANG Zheng, REN Longlong, LI Yang, et al. Design and experiment of load controller for chopping roller of hay cutter under disturbance[J].Transactions of the Chinese Society for Agricultural Machinery,2023,54(12):141-154.(in Chinese)
[16] JANG Lin, JOHN Lin. Mathematical model for improved mass flow estimation in the feeder housing of a forage harvester[D]. Illinois: The University of Illinois, 2012.
[17] 张认成, 桑正中. 轴流脱粒空间谷物运动仿真研究[J]. 农业机械学报, 2000, 31(1): 55-57. ZHANG Rencheng, SANG Zhengzhong. Simulation research on grain motion in axial threshing space[J].Transactions of the Chinese Society for Agricultural Machinery, 2000, 31(1):55-57.(in Chinese)
[18] 李文博. 橡胶传动带动态仿真及能耗机理研究[D]. 青岛:青岛科技大学,2019.LI Wenbo. Research on dynamic simulation and energy consumption mechanism of rubber transmission belt[D]. Qingdao: Qingdao University of Science and Technology,2019.(in Chinese)
[19] 马宪亭, 张福来. 液压系统中压力损失的分析与计算[J]. 煤矿机械, 2009, 30(9):26-28.MA Xianting, ZHANG Fulai. Analysis and calculation of pressure loss in hydraulic pressure system[J]. Coal Mine Machinery, 2009, 30(9):26-28.(in Chinese)
[20] 楚天舒, 杨增玲, 韩鲁佳. 中国农作物秸秆饲料化利用满足度和优势度分析[J]. 农业工程学报, 2016, 32(22): 1-9. CHU Tianshu, YANG Zengling, HAN Lujia. Analysis on satisfied degree and advantage degree of agricultural crop[J]. Transactions of the CSAE,2016,32(22):1-9.(in Chinese)
[21] FERRARETTO L F, SHAVER R D. Meta-analysis:effect of corn silage harvest practices on intake, digestion and milk production by dairy cows[J]. Professional Animal Scientist, 2012,28(3):624-637.
[22] WILKINSON J M, RINNE M. Highlights of progress in silage conservation and future perspectives[J]. Grass and Forage Science, 2018, 73(1): 40-52.
[23] 李法德, 邢书仑, 田富洋, 等. 齿辊式饲草作物调制试验台设计与试验[J]. 农业机械学报, 2021, 52(6): 136-147. LI Fade,XING Shulun,TIAN Fuyang,et al. Design and experiment of toothed roller forage crop conditioning test bench[J].Transactions of the Chinese Society for Agricultural Machinery,2021,52(6):136-147.(in Chinese)
[24] 胡良龙,王冰,王公仆,等.2ZGF-2型甘薯复式栽植机的设计与试验[J].农业工程学报, 2016, 32(10):8-16. HU Lianlong, WANG Bing, WANG Gongpu, et al. Design and experiment of type 2ZGF-2 duplex sweet potato trans planter[J]. Transactions of the CSAE, 2016, 32(10): 8-16. (in Chinese)
[25] WANG Zheng, GONG Qingfu, LI Fade, et al. Research on optimal control algorithm for power characteristics segmntation of forage harvester[J]. Inmateh-Agricultural Engineering, 2023,69(1):21-34.