0 引言
两平移一转动(2T1R)空间并联机构因其精度和灵活性较好,被广泛应用于装配、搬运和加工等场景中[1-4]。含冗余支链的并联机构可较好地避免奇异位置、稳定性高,具有较好的机构容错能力[5-10];同时,动平台输出无寄生运动有利于并联机构运动学、动力学分析[11-13]。
余顺年等[14]分析了一种2T1R并联机构,求得该机构运动学正反解的封闭解,并分析了工作空间内点转动能力;林浩等[15]根据基于方位特征集的并联机构拓扑设计理论与方法,综合出一批移动副为驱动的适用于铺盘调节机构的2T1R并联铺盘机构,它们具有符号式位置正解且部分运动解耦。覃才友等[16]分析了一种闭环支链冗余并联机构整体运动学性能,表明冗余支链虽会减小机构工作空间,但会提高机构整体结构刚度;TIAN等[17]设计了一种含中间变形肢的3-RPS/(H)并联机构,比单纯的3-RPS机构灵敏度和灵巧性高,但含有寄生运动,给分析、设计与标定带来困难。
上述机构中,同时具有冗余支链且无寄生运动的3-DOF 2T1R并联机构还较少。
目前,动力学模型建立方法主要有Lagrange法、Newton-Euler法、虚功原理法[18-21],其中,虚功原理法相较前两种方法过程更为简单和高效。李永泉等[22]针对一种空间被动过约束并联机构,采用牛顿欧拉法结合补充变形协调方程对其进行动力学建模分析;高洪等[23]基于刚体动力学牛顿-欧拉法建立了6-PSS并联机构逆运动学模型,比较空载和有载条件下算例仿真,验证了其模型的正确性。
本文基于方位特征(Position and orientation characteristics,POC)方程的并联机构设计理论,设计全由低副组成、含冗余支链但无寄生运动的3-DOF 2T1R并联机构,并对该机构进行动力学分析计算,以期为其后续的性能优化、结构设计和样机研制提供依据。
1 机构拓扑设计与分析
1.1 机构设计
本文设计一种3自由度2T1R机构,如图1所示,它由静平台0、动平台1以及连接两者的混合支链Ⅰ、Ⅱ组成,混合支链Ⅰ包含一个由分支链A(P1⊥R11‖R12)、分支链B(P2‖R21‖R22‖R23)并联组成的子并联机构1,R23的轴线经过且垂直于R12的轴线;又在其输出杆2末端串联连接轴线相互平行的R13、R14,且使R13(⊥R23)⊥R12,R14连接动平台1的一端;混合支链Ⅱ包含一个由分支链C(P3⊥R31‖R32)、冗余支链D(P4⊥R41‖R42)并联组成的子并联机构2,又在其输出杆3的末端串联连接R33,且用R33连接动平台1的另一端。
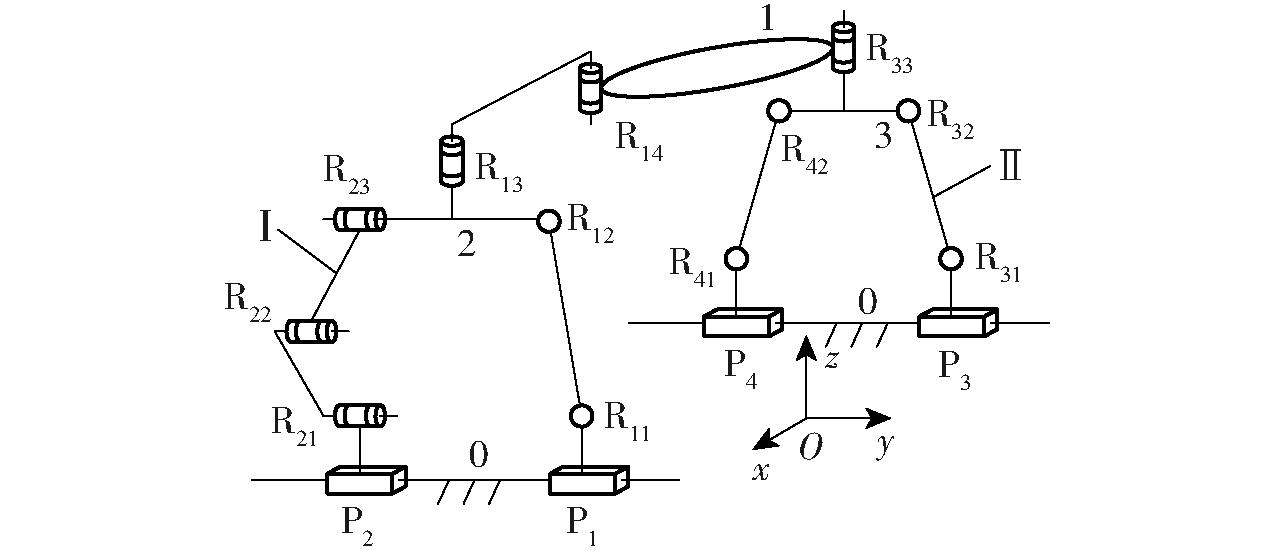
图1 3-DOF 2T1R机构
Fig.1 3-DOF 2T1R mechanism
进一步,混合支链Ⅰ中的移动副P1、P2,以及混合支链Ⅱ中的移动副P3、P4分别位于两根平行于y轴的导轨上,动平台1上的转动副R14、R33轴线平行。
1.2 机构拓扑
1.2.1 机构POC集设计
串、并联机构POC方程[24]分别为
(1)
(2)
式中 MJi——第i个运动副的POC集
Mbi——第i条支链末端的POC集
MPa——机构动平台的POC集
选定动平台1上R33轴线上任意一点为基点O′。
混合支链Ⅰ中,子并联机构1的中间杆2输出运动为两平移(2T);与R13‖R14串联后,其末端输出为三平移一转动(3T1R)。
混合支链Ⅱ中,子并联机构2的中间杆3输出运动为两平移一转动(2T1R),串联R33后,末端输出为两平移两转动(2T2R)。
因此,混合支链Ⅰ、Ⅱ末端构件的POC集由式(1)、(2)可得
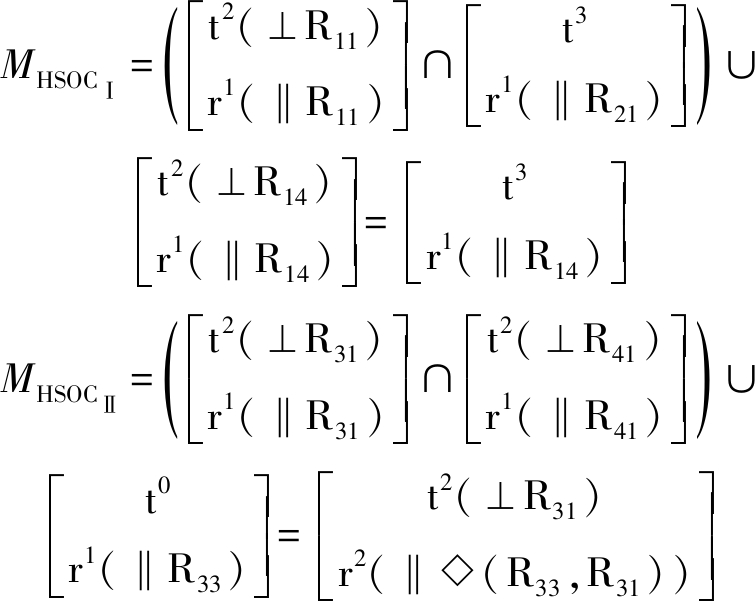
因此,动平台POC集由式(2)得
(3)
由式(3)知,机构动平台1具有YOZ平面内两维移动以及绕转动副R14轴线转动的特性,可见其无寄生运动。
1.2.2 自由度
并联机构非瞬时自由度计算式[24]为
(4)
其中![]()
(5)
式中 F——机构自由度
fi——第i个运动副自由度
ν——独立回路数
ξLj——第j个独立回路独立位移方程数
![]() 前j条支链组成的子并联机构POC集
前j条支链组成的子并联机构POC集
Mb(j+1)——第j+1条支链末端构件POC集
第1回路为混合支链Ⅰ中的子并联机构,即
Loop1{-P1⊥R11‖R12⊥R23‖R22‖R21‖P2-}
其独立位移方程数ξL1可由式(5)求得
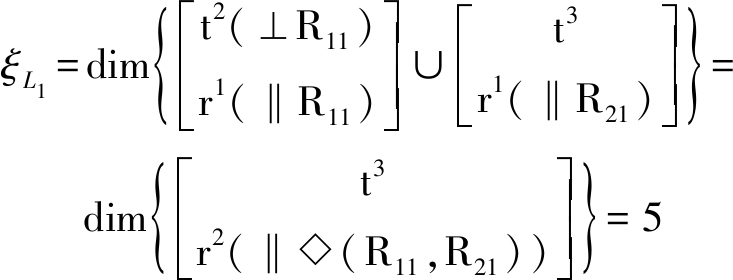
第2回路(即第2子并联机构)由上述混合支链(含第1个子并联机构、子串R13‖R14‖R33)及分支链C(P3⊥R31‖R32)组成,即
Loop2{-R13‖R14‖R33⊥R32‖R31⊥P3-}
其独立位移方程数ξL2可由式(5)求得
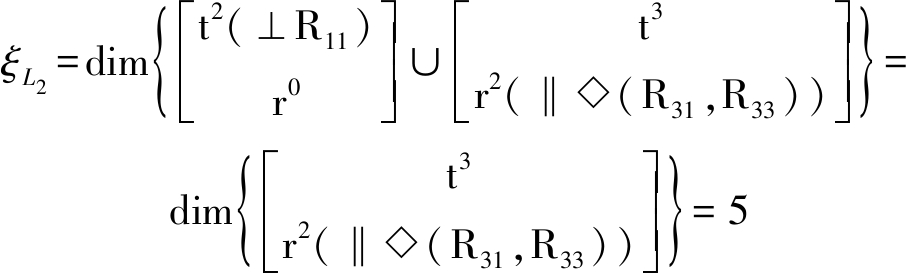
第3回路由上述第2个子并联机构和分支链D组成,其独立位移方程数ξL3为
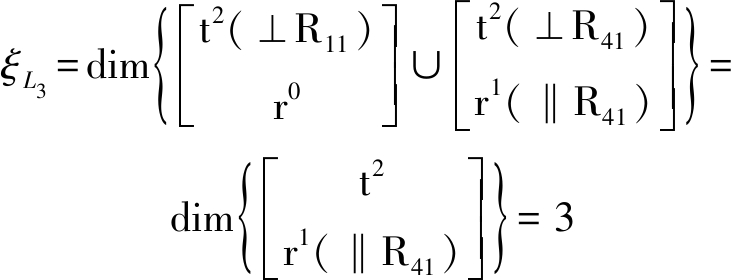
由式(4)可得机构自由度为
因此,该机构自由度为3, 当取静平台0上的移动副P1、P2、P3为驱动副时,机构动平台1可实现YOZ面内两维平移和绕R14轴线的转动输出,无寄生运动。
1.2.3 耦合度κ计算
由基于序单开链(SOC)单元的机构组成原理知,一个机构可分解为若干个最小子运动链(Sub-kinematic chain, SKC);而一个SKC又可分解为若干个单开链,第j个单开链SOCj的约束度定义[25]为
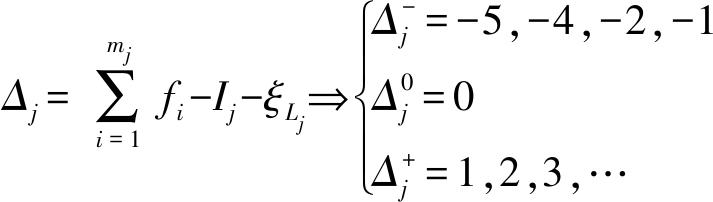
(6)
式中 mj——第j个SOCj运动副数量
fi——第i个运动副自由度
Ij——第j个SOCj驱动副数量
SKC耦合度为
(7)
上述3个回路约束度由式(6)分别计算得
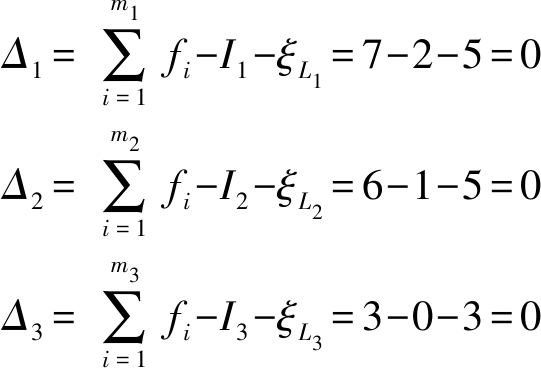
由SKC判定准则可知,该机构由3个SKC组成,由式(7)分别求得耦合度为
该机构耦合度为零,可求得符号式位置正解。
进一步,该机构拓扑结构解析表示为[25]
(8)
另外,动平台y、z轴向位置仅由P1、P2确定,而绕R14轴线转角则由P1、P2、P3确定。因此,该机构具有部分运动解耦性,运动控制容易。
2 位置正反解
机构运动学建模如图2所示,设静平台0两导轨间距为2a,动平台E1F1长度为b,且lAiBi=l1(i=1,2,3,4),lB1C1=l2,lB2C2=lC2D2=l3,lB3C3=lB4C4=l4,lC1D1=lD1D2=lC3D3=lD3C4=l5,lD1E1=lD3E3=l6,lE1F1=l7。
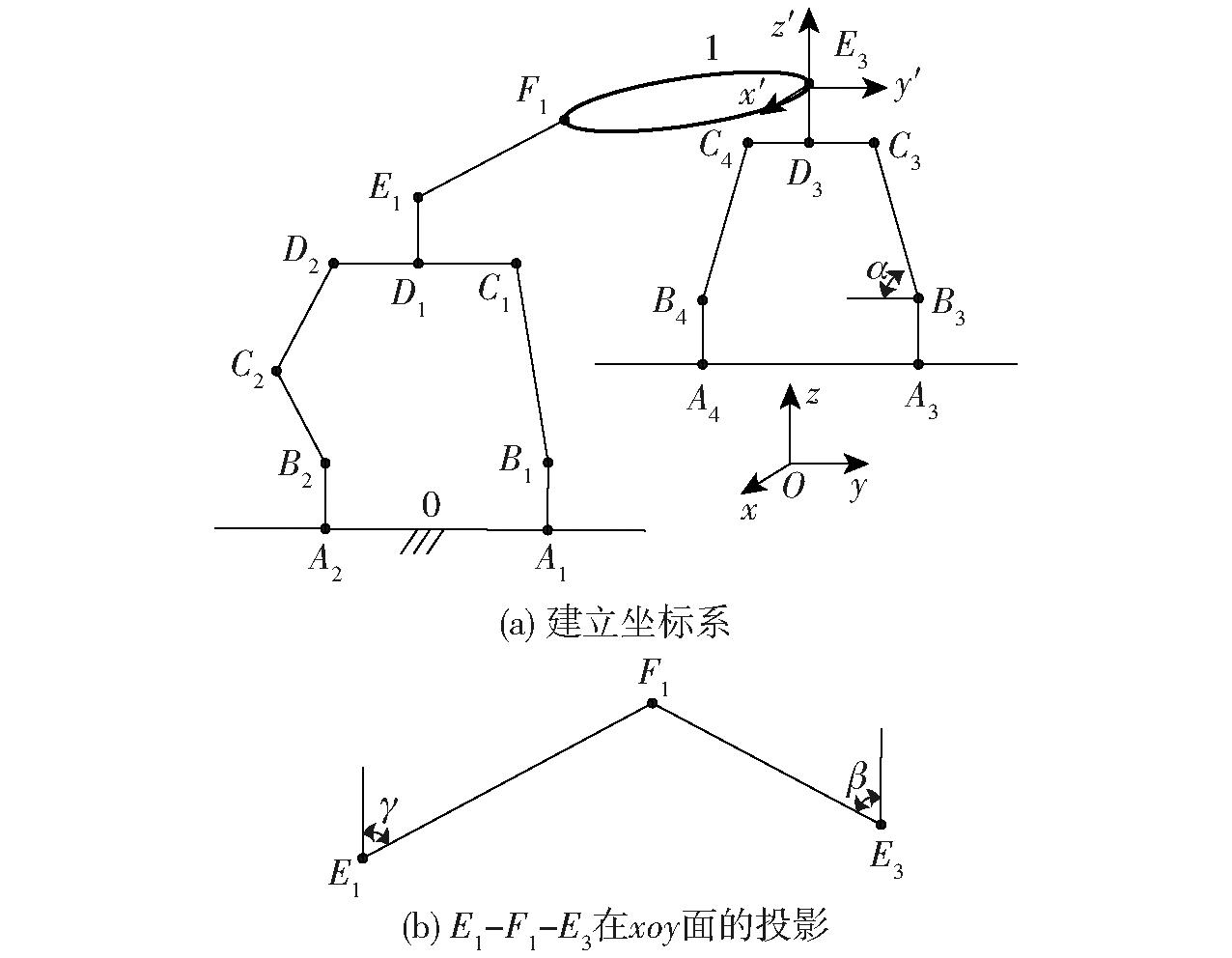
图2 机构运动学建模
Fig.2 Kinematics modeling of mechanism
取两导轨平行线之平分线上一个定点为静坐标系原点,建立笛卡尔静坐标系Oxyz,动平台1上基点E3作为动坐标系原点O′,x′、y′轴分别重合、垂直E3F1,z′轴由右手定则确定。
2.1 位置正解
机构位置正解为:已知静平台上3个点Ai(i=1,2,3)的移动位置yA1、yA2、yA3,求动平台1上O′点的坐标(x,y,z)及姿态角β。
在静坐标系中,易知
A1=(a,yA1,0) A2=(a,yA2,0) A3=(a,yA3,0)
B1=(a,yA1,l1) B2=(a,yA2,l1) B3=(a,yA3,l1)
D2=(a,yA2,z-l6) C1=(a,yA2+2l5,z-l6)
由杆长约束条件lB1C1=l2,解得
(9)
由拓扑约束易知:yD3=yE3,可求得
y=yA3-l4cosα-l5
(10)
设B3C3与y轴负向夹角为α,可得点C3、D3坐标为
C3=(-a,yA3-l4cosα,l1+l4sinα)
D3=(-a,yA3-l4cosα-l5,l1+l4sinα)
由拓扑分析zD3=zE3+l6,可解得α为
(11)
对于姿态角β,结合点E1、F1、F3在xOy面内的坐标,可得方程组
(12)
解得![]()
(13)
其中
A=4ab B=-2ub
![]()
u=yA2+2l5-yA3+l4cosα
至此,动平台1上点O′坐标(x,y,z)及姿态角β已全部解出,且有
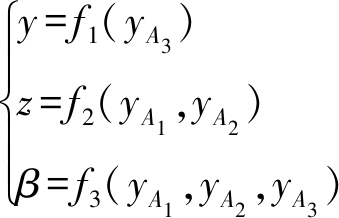
(14)
由式(14)可知,该机构不仅有符号式位置正解,而且具有部分运动解耦性,即输出端点O′的y值仅由输入量yA3决定,z值仅由yA1、yA2决定,β由yA1、yA2、yA3共同确定。
2.2 位置逆解
机构位置逆解为:已知动平台1上点O′坐标(x,y,z)及姿态角β,求静平台上3个点Ai(i=1,2,3)移动位置yA1、yA2、yA3。
由式(10)可求得
yA3=y+l4cosα+l5
(15)
由式(12)可求得
yA2=yA3-l4cosα-bcosβ-2l5+l7cosγ
(16)
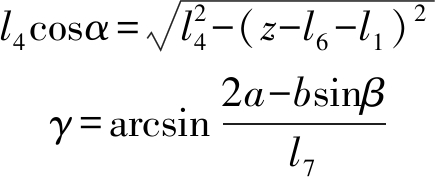
由式(9)可求得
(17)
至此,机构位置逆解yA1、yA2、yA3已解出。
2.3 正逆解数值验算
设机构尺寸参数为:a=60 mm,b=100 mm,l1=20 mm,l2=l3=l4=50 mm,l5=37.5 mm,l6=20 mm,l7=60 mm。
根据上述尺寸参数,从该并联机构3D模型中测量得3个驱动副P1、P2、P3的输入值分别为yA1=26.84 mm、yA2=-67.84 mm、yA3=56.75 mm,将此代入正解式(14),利用Matlab软件编程,得到4组位置实数正解,如下:①y=-0.430 0 mm,z=85.964 1 mm,β=0.825 5 rad。②y=-0.430 0 mm,z=-5.964 1 mm,β=0.825 5 rad。③y=-0.430 0 mm,z=-5.964 1 mm,β=1.827 5 rad。④y=-0.430 0 mm,z=85.964 1 mm,β=1.827 5 rad。
由Solidworks三维模型知,第①组数据符合实际构型,故将第①组正解代入式(15)~(17),得到2组反解输入值为:①yA1=26.839 8 mm,yA2=-67.840 1 mm,yA3=56.750 0 mm。②yA1=-12.520 1 mm,yA2=-67.840 1 mm,yA3=56.750 0 mm。
易知,第①组反解结果与3个输入测量值一致。进一步,设3个驱动副运动规律分别为yA1=30sint,yA2=20sint,yA3=30sin2t,得到该机构动平台基点O′在时间t=10 s内,y、z向位移理论与仿真值曲线一致,如图3a所示;以及姿态角β的理论与仿真曲线一致,如图3b所示,因此,验证了正解公式和反解公式的正确性。
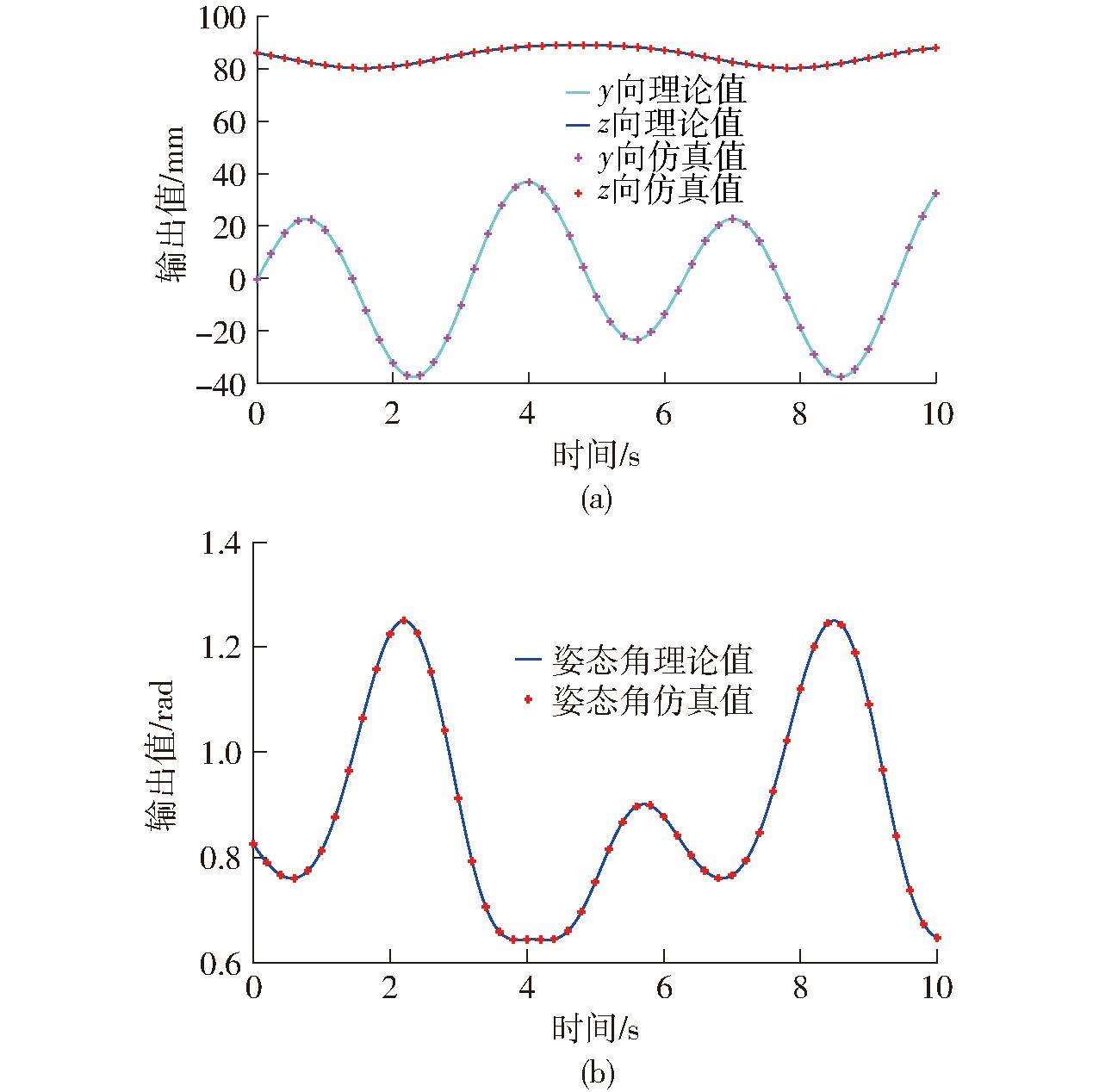
图3 机构动平台位姿y、z、β的对比
Fig.3 Comparison of postures y, z and β of moving platform of mechanism
2.4 速度、加速度
设机构基点输出速度![]() 驱动副输入速度
驱动副输入速度![]() 则对杆长约束条件lB1C1=l2,式(10)、(12)的位置方程全微分后可表示为
则对杆长约束条件lB1C1=l2,式(10)、(12)的位置方程全微分后可表示为
(18)
其中
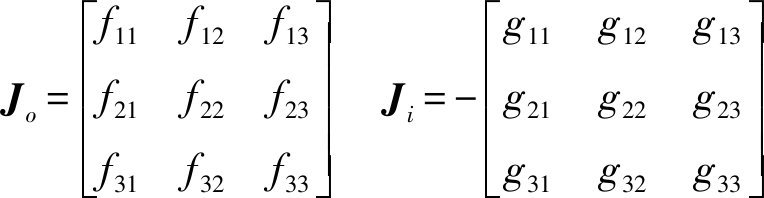
f11=0 f12=2(z-l6-l1) f13=0
f21=2(y-yA2-bcosβ-l5) f22=0
f23=2bcosβ(bsinβ-2a)-2bsinβ(yA2-y+bcosβ+l5)![]()
g11=2(yA1-yA2-2l5) g12=2(yA2-yA1+2l5)
g13=0 g21=0
g22=2(yA2-y+bcosβ+l5) g23=0
g31=0 g32=0 g33=1
机构非奇异时,Jo可逆,由式(18)可得
(19)
对式(19)中时间t求导可得
(20)
其中![]()
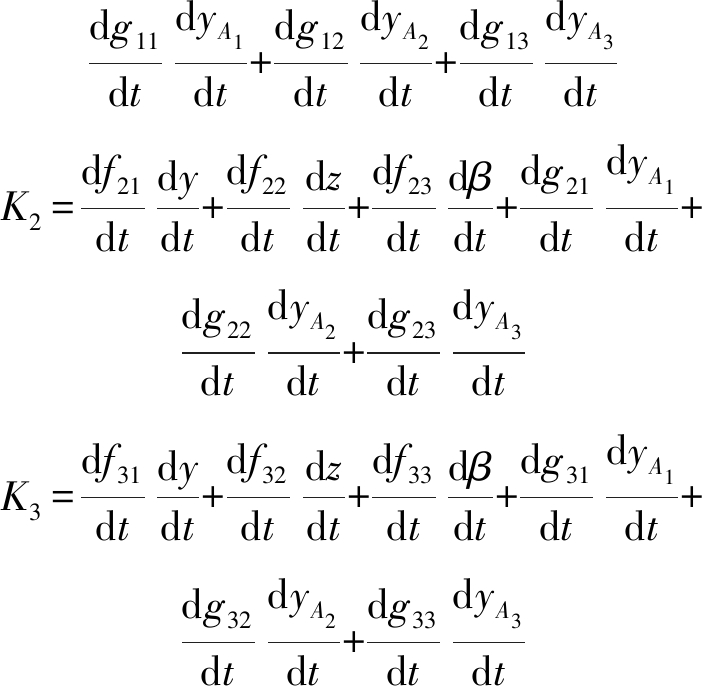
利用Matlab软件对式(19)、(20)编程,以及ADAMS软件生成虚拟样机,可得到动平台基点速度、加速度(略),已验证一致。其中,驱动副运动规律同2.3节。
3 奇异性和工作空间
3.1 奇异性
根据矩阵Jo和Ji是否奇异,将机构奇异分为3种类型:当det(Ji)=0时,机构发生输入奇异;当det(Jo)=0时,机构发生输出奇异;当det(Jo)=det(Ji)=0时,机构发生综合奇异。
(1)输入奇异
当det(Ji)=0时,机构发生输入奇异,因为Ji为上三角矩阵,故有2种情况:
①![]() 即点A1与A2的y=75.0 mm,如图4a所示。
即点A1与A2的y=75.0 mm,如图4a所示。
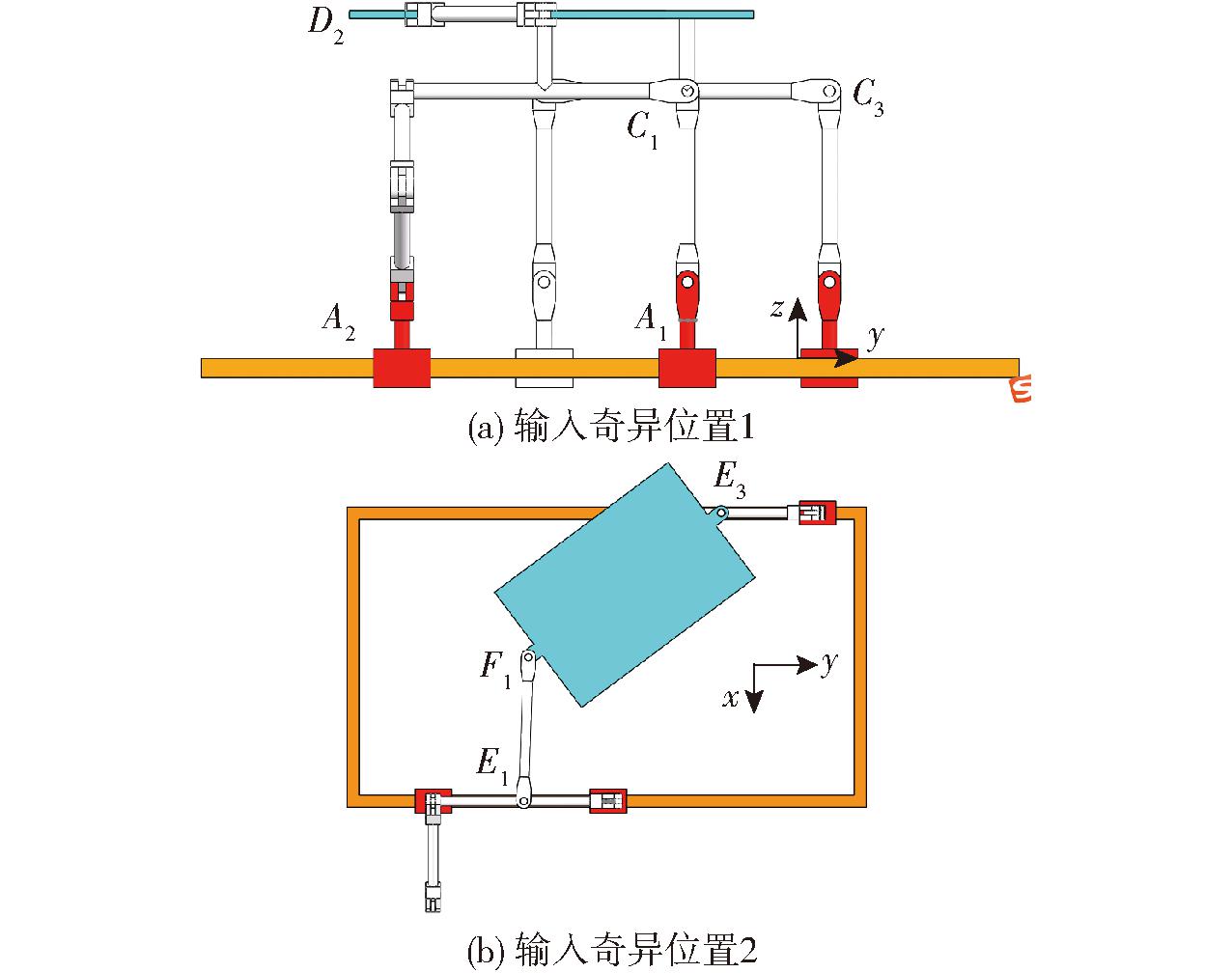
图4 输入奇异位置
Fig.4 Input singular position
②![]() 即点F1与A2的y=37.5 mm,如图4b所示。
即点F1与A2的y=37.5 mm,如图4b所示。
当机构发生输入奇异时,意味着每条支链靠近驱动副杆的被动杆与驱动杆,这两杆处于共线或平行状态,此时,动平台自由度数减少,运动失控。
(2)输出奇异
当det(Jo)=0时,机构发生输出奇异,根据Jo矩阵特性,有2种情况:
①![]() 即基点的z=40 mm。
即基点的z=40 mm。
②![]() 即姿态角满足β=
即姿态角满足β=![]() 时,机构发生输出奇异。
时,机构发生输出奇异。
(3)综合奇异
当det(Jo)=det(Ji)=0时,机构发生综合奇异,即f12=g22=0,此时,基点z=40.0 mm且F1与点A2的y=37.5 mm。
3.2 工作空间
利用位置正解求解机构的可达工作空间的方法,具有计算量少、边界准确等优点[14],其步骤是:先预设驱动副输入范围,取:-50 mm≤yA1≤80 mm,-100 mm≤yA2≤10 mm,0≤yA3≤100 mm;再通过Matlab编程求解满足所有约束条件的点,并将这些点绘成三维图,即为动平台质心处工作空间,如图5a所示。进一步,分别选取x=-60 mm、y=80 mm、z=50 mm,得到3个截面图如图5b~5d,表明:①该机构具有连续、规则的工作空间。②在设定驱动副输入范围下,工作空间x轴方向范围为[-110 mm, -10 mm],y轴方向范围为[-140 mm, 60 mm],z轴方向范围为[40 mm, 90 mm]。

图5 机构工作空间
Fig.5 Mechanism workspaces
4 机构动力学
4.1 各杆件速度和加速度
动平台1质心速度和加速度为
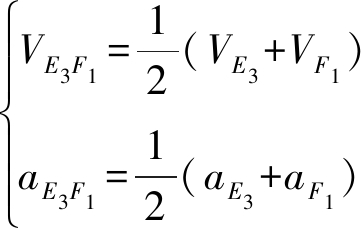
(21)
动平台角速度和角加速度为
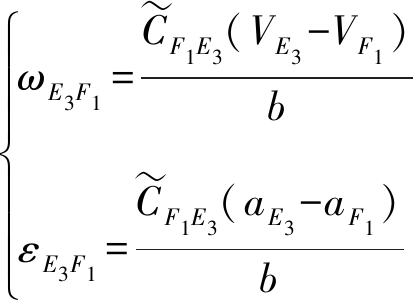
(22)
点E3和点F1速度和加速度可由速度、加速度合成定理逐步求得。
机构中其余构件速度和加速度与上述类似,在此从略。
4.2 机构动力学建模
4.2.1 动力学建模方法
基于虚功原理的序单开链法对自由度为f、广义速度为![]() 的机械系统,基于单开链(SOC)的机构组成原理,将其分解为若干个子运动链(SKC),而每一个子运动链又可拓扑分解为若干个单开链
的机械系统,基于单开链(SOC)的机构组成原理,将其分解为若干个子运动链(SKC),而每一个子运动链又可拓扑分解为若干个单开链![]() 假定解除原系统若干个运动副的k个约束后,解除的运动副支反力将转换为作用在新系统构件上的未知力。相应新系统增加的广义速度记作
假定解除原系统若干个运动副的k个约束后,解除的运动副支反力将转换为作用在新系统构件上的未知力。相应新系统增加的广义速度记作![]()
按照上述拓扑结构分解的逆序,对单开链进行动力学分析,由单开链之间的约束关系和虚功原理可知:在理想约束下,外力(矩)和惯性力(矩)在机械系统的任何虚位移上的元功之和等于零,即可建立各SKC的动力学分析方程。
4.2.2 受力分析
该并联机构由3个零耦合度的SKC组成,其中SKC3为冗余支链,可分别在SKC1、SKC2内对各杆件进行受力分析,具体如下:
(1)SKC2内各杆件受力分析
对移动滑块A3B3有
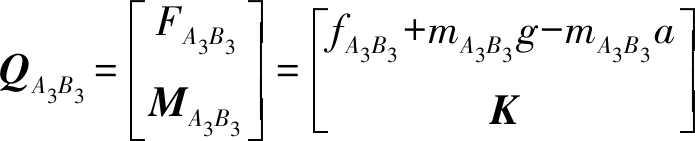
其中
式中 mA3B3——滑块A3B3质量
fA3B3——滑块A3B3上驱动力
对杆件B3C3有
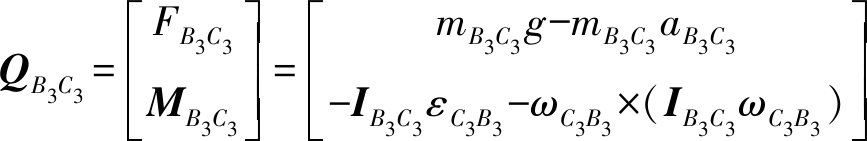
式中 mB3C3——滑块B3C3质量
IB3C3——杆B3C3相对于Oxyz坐标系的惯量矩阵
取动平台的质心为点p,则
式中 fp、τp——所受的外力和外力矩
mp——动平台质量 g——重力加速度
ω1、ε1——动平台角速度和角加速度
Ip——动平台相对于坐标系Oxyz的惯量矩阵
对杆件E1F1有
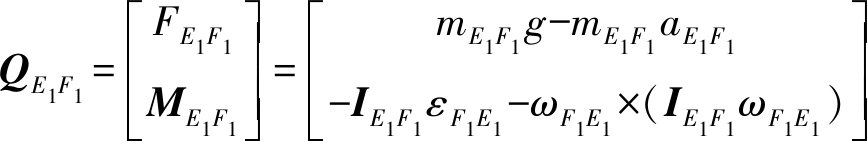
式中 mE1F1——滑块E1F1质量
IE1F1——杆E1F1相对于Oxyz坐标系惯量矩阵
(2)SKC1内各杆件受力分析
由于杆件D2D1、D1C1、D1E1均在yOz面内运动,且无转动,故将三者看作1根杆D2C1,可得
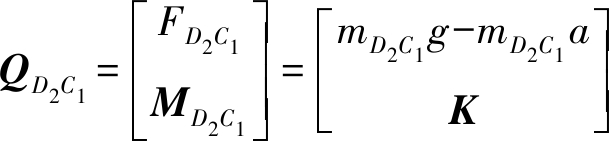
对杆件B1C1有
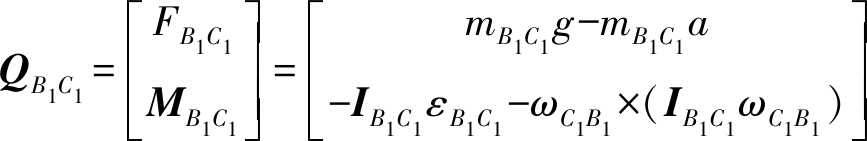
式中 mB1C1——滑块B1C1质量
IB1C1——杆B1C1相对于Oxyz坐标系的惯量矩阵
对杆件B2C2有
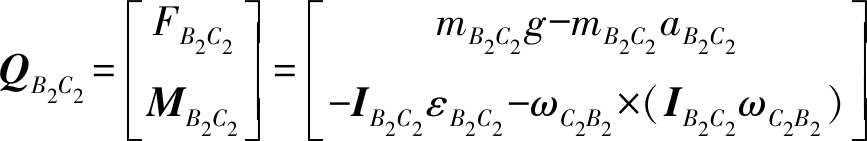
式中 mB2C2——滑块B2C2质量
IB2C2——杆B2C2相对于Oxyz坐标系的惯量矩阵
对杆件C2D2有
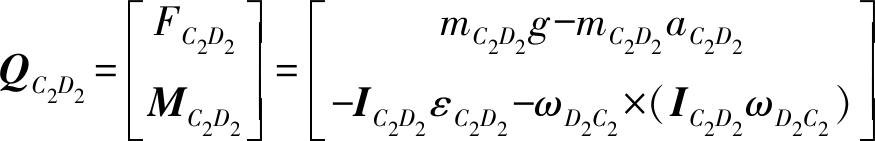
式中 mC2D2——滑块C2D2质量
IC2D2——杆C2D2相对于Oxyz坐标系的惯量矩阵
对驱动滑块AiBi(i=1,2)有
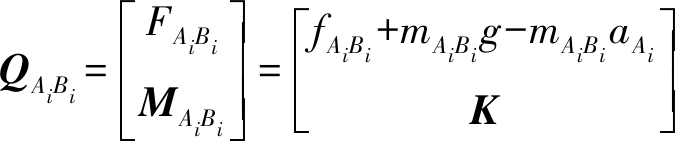
式中 mAiBi——滑块AiBi质量
fAiBi——滑块AiBi上驱动力
4.2.3 动力学方程建立
解除运动副R13(点E)的约束,得到SKC1、SKC2两个子系统,则支反力FE转换为作用在该两个子系统构件上的未知外力。基于虚功原理的序单开链法,分别在两个子系统中建立动力学方程。
SKC2动力学方程为
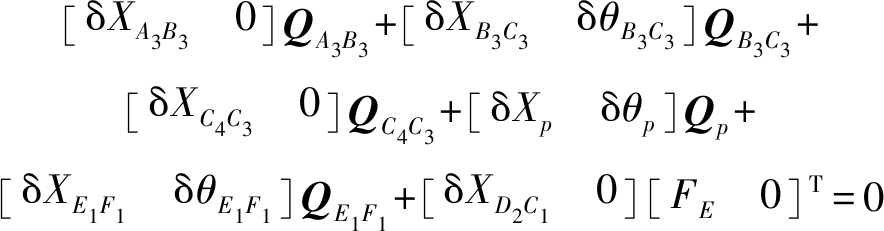
(23)
SKC1动力学方程为
![]()
![]()
(24)
其中
δXAiBi=JvAiBiδq (i=1,2,3)
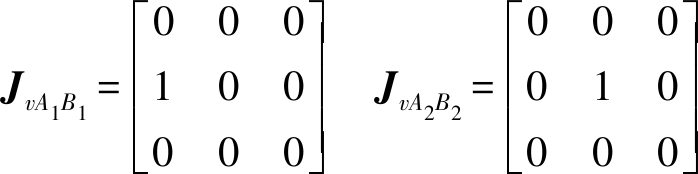
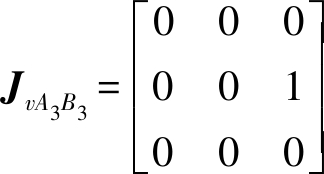
δXBiCi=JvBiCiδq (i=1,2,3)
δθBiCi=JωCiBiδq δXC2D2=JvC2D2δq
δθC2D2=JωD2C2δq δXD2C1=JvD2C1δq
δXC4C3=JvC4C3δq δXE1F1=JvE1F1δq
δθE1F1=JωF1E1δq δXp=Jvpδq δθp=Jωpδq
式中 FE——支反力
4.3 驱动力计算实例
4.3.1 杆件参数
设机构中各杆件质量分别为mAiBi=1.517 5 kg,mB1C1=0.825 3 kg,mB2C2=0.825 3 kg,mC2D2=0.973 5 kg,mD2C1=1.354 5 kg,mB3C3=0.825 3 kg,mC3D3=1.519 3 kg,mE1F1=1.099 2 kg,mE3F1=10.948 3 kg(含动平台自重以及外加5 kg负载)。杆件转动惯量如表1所示。
表1 各杆件转动惯量参数
Tab.1 Moment of inertia parameters of each member kg·mm2
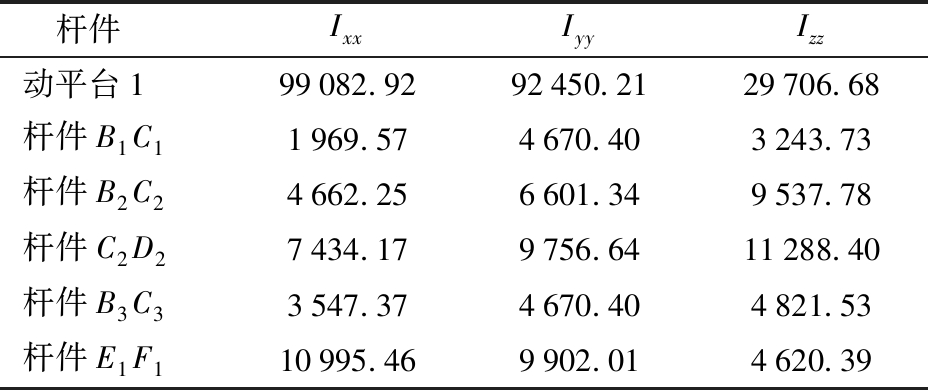
杆件IxxIyyIzz动平台199082.9292450.2129706.68杆件B1C11969.574670.403243.73杆件B2C24662.256601.349537.78杆件C2D27434.179756.6411288.40杆件B3C33547.374670.404821.53杆件E1F110995.469902.014620.39
4.3.2 驱动力求解
使用上述参数,利用Matlab对上述动力方程进行编程,驱动副输入规律同2.3节,可得到驱动力理论曲线,如图6a所示。
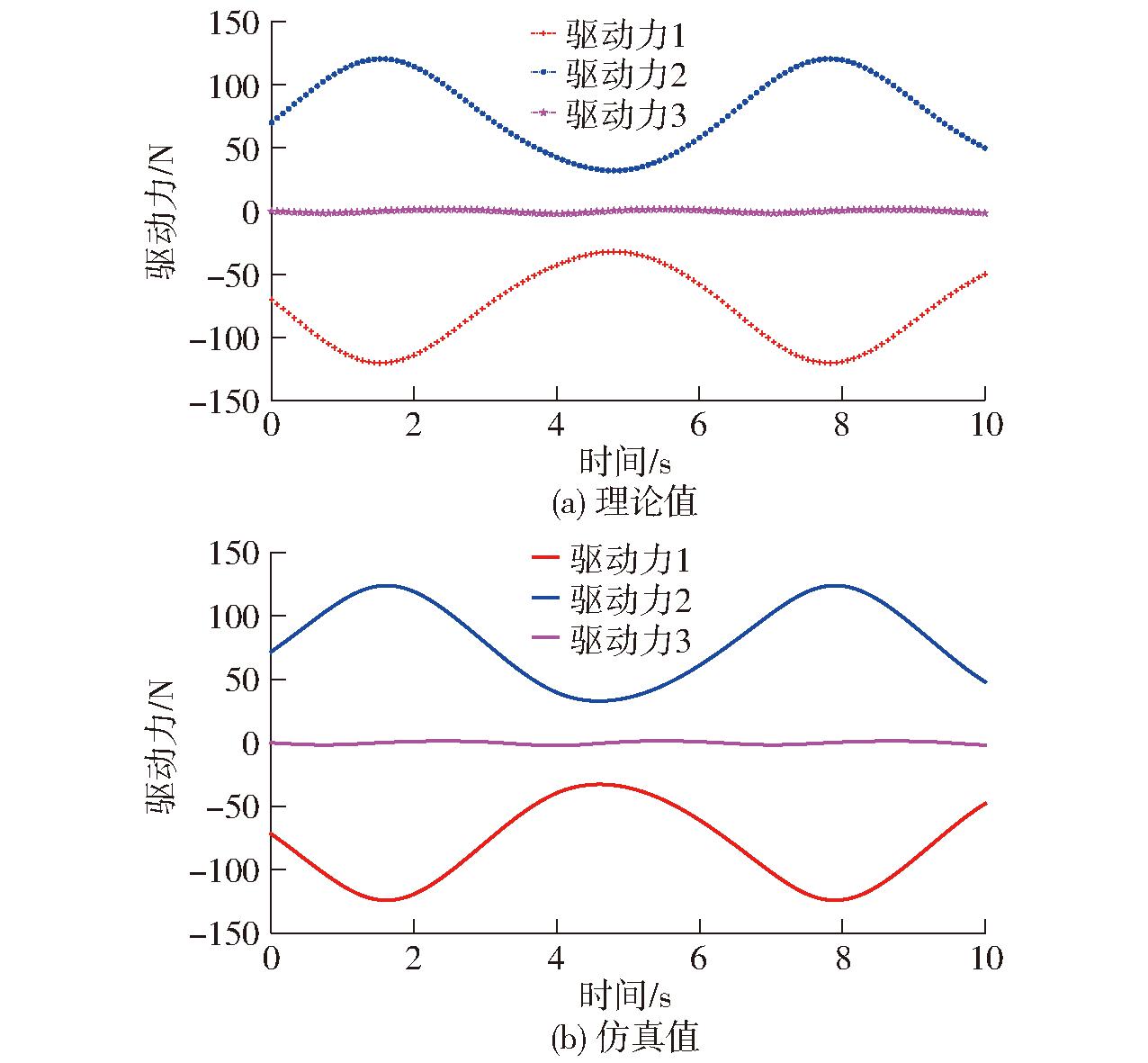
图6 驱动力曲线
Fig.6 Driving force curves
同样,对ADAMS建立的虚拟样机进行仿真,可得到驱动副驱动力的仿真曲线如图6b所示。可拟合近似得到驱动力随时间变化的函数为
F1(t)=79.33sin(0.14t-2.24)+49.13sin(0.96t-2.97)
F2(t)=79.47sin(0.14t+0.90)+49sin(0.96t+0.17)
F3(t)=1.66sin(2.01t-3.17)+0.18sin(3.02t-1.78)
经比较发现:3个驱动力理论值和仿真值吻合,误差在1.6%左右,因此,认为动力学模型正确。
由图6可知,3个滑块所需最大驱动力分别为124.056 7、123.9、1.5 N,为驱动电机选择奠定了技术基础。
解除点E的约束后,支反力FE转换为未知外力,根据式(23)、(24)可得到点E处z向支反力理论值与仿真值曲线,如图7所示。
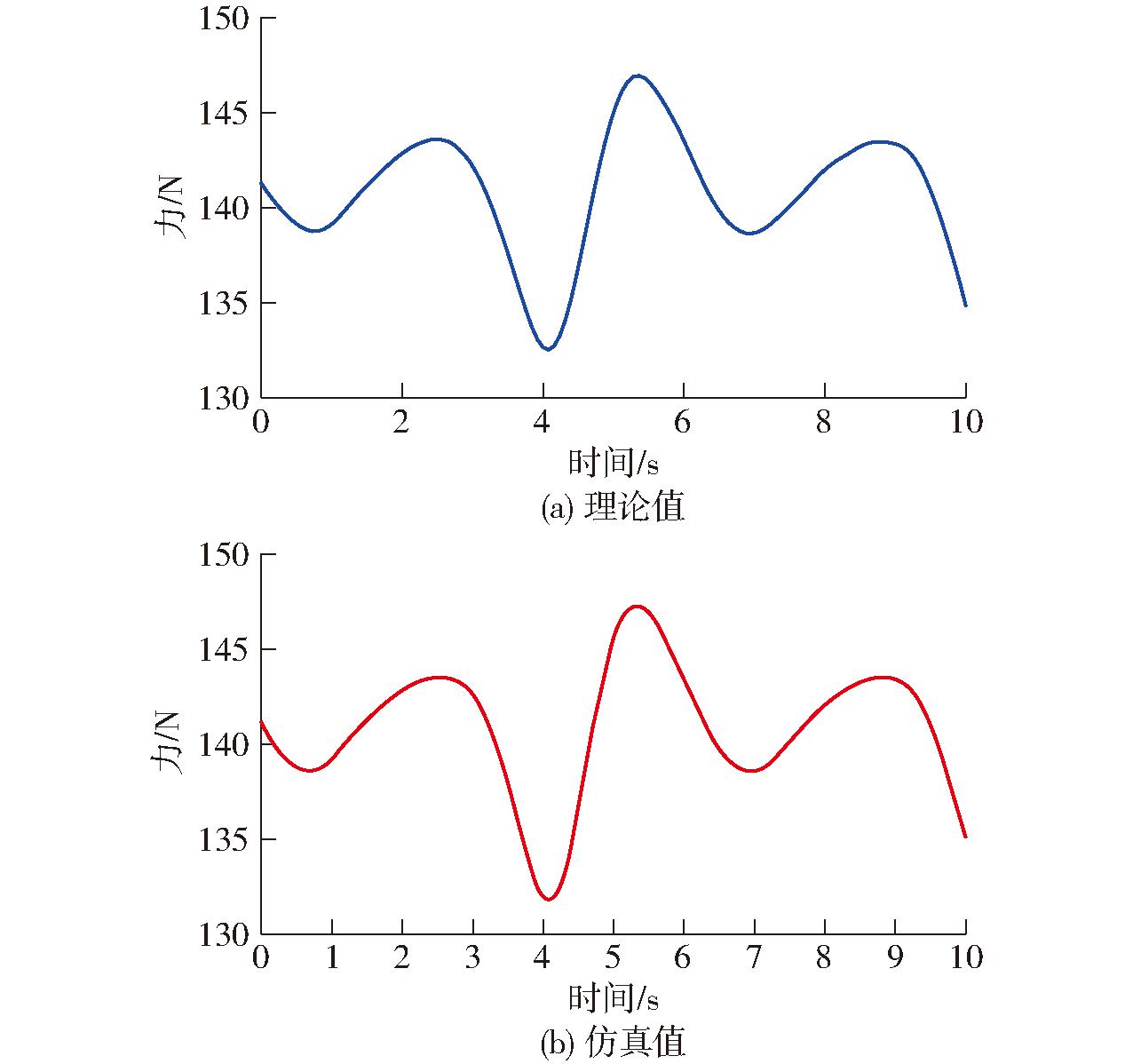
图7 支反力曲线
Fig.7 Support reaction force curves
对比点E处z方向支反力理论值和仿真值可知,两者误差为2.2%左右,较为合理。
5 机构应用概念设计
军事训练需用射击靶,固定靶存在的缺点是:①位置和姿态恒定,不能充分展示射击者应对不同目标的能力。②限制射击者对目标追踪和命中能力的锻炼。因本文设计的2T1R机构可同时变化位置和姿态,适应射击靶训练要求机构运动准确、所需位置和姿态的快速变化需求,而对所承受负载以及机构自身刚度要求不大。因此,满足军事远程训练的射击活动靶的需求,其概念设计如下:
2根平行导轨固定在远处(野外或室内的支撑壁上),靶标固定放置在动平台上,该机构整体在3个驱动副运动下成为活动靶,士兵在一定距离外进行远程打靶。
该活动靶具有的优势为:①可在导轨方向长距离移动,适用于多组人员在不同的地点进行训练,以提高训练的人数与效率,降低训练成本。②可提供靠近或远离方向的移动,以及姿态角的变化,可提高官兵射击的训练难度、分等级训练,以及训练的实效。
图8展示了正视角下该活动靶在2个平行导轨上的任意3个位置,红色虚线为机构被人形靶遮住部分,红色为该装置组成部分,蓝色箭头注明了正视角下靶牌运动变化,包括:沿导轨左右方向移动(a);沿垂直于导轨的靠近或远离方向移动(b);机构动平台姿态角变化运动(c)。
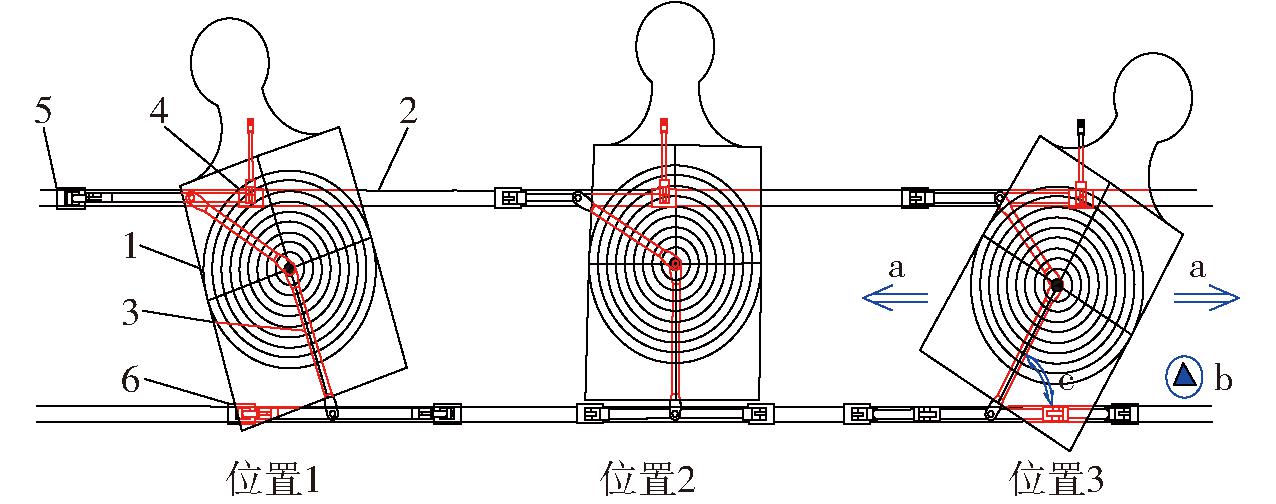
图8 机构应用与概念设计
Fig.8 Mechanism application and conceptual design
1.人形靶 2.静平台0 3.动平台1 4.驱动滑块1 5.驱动滑块2 6.驱动滑块3
6 结论
(1)该机构设计与制造方便、刚度好;耦合度为零,具有符号式位置正解,以及部分运动解耦性,这些特性有利于机构实时控制和运动轨迹规划。
(2)基于拓扑特征的运动学建模方法,得到了该机构速度、加速度,分析了其奇异性及工作空间等特性。
(3)基于虚功原理的序单开链法,建立动力学模型,得到3个驱动副所需的驱动力,及其2个SKC连接处的支反力,并利用ADAMS仿真,验证了该动力学模型的正确性。
(4)提出了该机构用于军事远程训练射击活动靶的概念设计场景,对提高射击训练方式和实效具有启发意义。
[1] 刘伟,曹亚斌.转轴轴线可变的2T1R并联机构运动模式分析[J].包装工程,2020,41(13):192-196.LIU Wei, CAO Yabin. Motion mode of 2T1R parallel mechanism with a variable rotation axis[J]. Packaging Engineering,2020,41(13):192-196.(in Chinese)
[2] WANG Dongbao, ZHANG Jing, GUO Hongwei, et al.Design of a 2T1R-type parallel mechanism: performance analysis and size optimization[J]. Actuators,2022,11(9):262.
[3] 杜中秋,沈惠平,李菊,等.一种位置正解符号化且运动部分解耦的新型2T1R并联机构动力学分析[J].机电工程,2023,40(8):1231-1239.DU Zhongqiu, SHEN Huiping, LI Ju, et al. Dynamics analysis of a new 2T1R parallel mechanism with symbolic position solutions and partially motion decoupled[J]. Journal of Mechanical &Electrical Engineering, 2023,40(8):1231-1239.(in Chinese)
[4] YAN Y, LUO F Y,SHI X Z, et al.Structure synthesis of two-translation and two-rotation parallel mechanisms based on the POC-based approach[J].Applied Mechanics and Materials,2011,1229(52-54):759-767.
[5] 王世杰,冯伟,李铁军,等.空间2自由度冗余驱动并联机构运动学性能分析[J].机械工程学报,2022,58(23):18-27.WANG Shijie, FENG Wei, LI Tiejun, et al. Kinematic performance analysis of spatial 2-DOF redundantly actuated parallel manipulator[J]. Journal of Mechanical Engineering, 2022,58(23):18-27.(in Chinese)
[6] 冯建彬,李铁军,杨冬,等.冗余驱动并联机构的驱动力协调性优化控制方法[J].制造业自动化,2022,44(10):79-83.
[7] 姜丙山.面向特定任务需求的冗余驱动并联机构构型设计与控制方法研究[D].北京:北京交通大学,2022.JIANG BingShan. Research on structural design and control method of redundant actuated parallel mechanism for task-specific requirements[D]. Beijing: Beijing Jiaotong University, 2022. (in Chinese)
[8] 王耀军.一类冗余驱动少自由度并联机构的动力学建模与控制[D].杭州:浙江理工大学,2021.WANG Yaojun. Dynamics modeling and control of a class of redundantly-actuated parallel mechanisms[D]. Hangzhou: Zhejiang Scitech University, 2021.(in Chinese)
[9] 叶伟,胡利焕,夏董新,等.冗余驱动的三平动并联机构性能分析与优化[J].农业机械学报,2021,52(11):421-430.YE Wei, HU Lihuan, XIA Dongxin, et al. Performance analysis and optimization of redundantly actuated three translational parallel mechanism[J].Transactions of the Chinese Society for Agricultural Machinery,2021,52(11):421-430.(in Chinese)
[10] 王新智.基于冗余结构的并联抓取机器人的设计与分析[D].北京:北京交通大学,2022.WANG Xinzhi. Design and analysis of parallel manipulator based on redundant structure[D]. Beijing: Beijing Jiaotong University, 2022. (in Chinese)
[11] WU Zhen, CHEN Qiaohong, YE Wei. Modeling and performance analysis of elastostatic stiffness of kinematically redundant parallel mechanisms[J].Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science,2024,238(1):123-137.
[12] 杨廷力.机械系统基本理论-结构学、运动学、动力学[M].北京: 机械工业出版社,1996.
[13] 邓嘉鸣,许可,赵迎春,等.无寄生运动非对称空间2T1R并联机构设计与运动学分析[J].农业机械学报,2018,49(6):408-417.DENG Jiaming, XU Ke, ZHAO Yingchun,et al. Design and kinematics analysis of asymmetric 2T1R-type spatial parallel mechanism without parasitic motion[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018,49(6):408-417.(in Chinese)
[14] 余顺年,马履中.两平移一转动并联机构位置及工作空间分析[J].农业机械学报,2005, 36(8):103-106.YU Shunnian, MA Lüzhong. Position and workspace analysis of parallel mechanism with two translational and one rotational degree of freedom[J]. Transactions of the Chinese Society for Agricultural Machinery, 2005, 36(8):103-106.(in Chinese)
[15] 林浩,石志新,罗玉峰,等.可用于铺盘调节的2T1R并联机构的综合与运动学分析[J].机械传动,2022,46(5):48-52,99.LIN Hao, SHI Zhixin, LUO Yufeng, et al. Synthesis and kinematics analysis of a 2T1R parallel mechanism that can be used for spreading tray adjustment[J]. Journal of Mechanical Transmission, 2022,46(5):48-52,99.(in Chinese)
[16] 覃才友,黄娟,李小汝.一种新型闭环支链冗余并联机构[J].机械传动,2019,43(7):84-90.QIN Caiyou, HUANG Juan, LI Xiaoru. A new type of closed-loop limb redundant parallel mechanism[J]. Journal of Mechanical Transmission, 2019,43(7):84-90.(in Chinese)
[17] TIAN Haibo, WANG Chengyu, MA Hongwei, et al.Kinematic analysis and workspace investigation of novel 3-RPS/(H) metamorphic parallel mechanism[J]. Journal of Mechanisms and Robotics,2011,59(2):1-19.
[18] 沈惠平,朱晨阳,李菊,等.零耦合度部分运动解耦2T1R并联机构拓扑与性能研究[J].农业机械学报,2023,54(2):419-429,440.SHEN Huiping, ZHU Chenyang,LI Ju, et al. Topology and performance analysis of 2T1R parallel mechanism with zero coupling degree and motion decoupling[J]. Transactions of the Chinese Society for Agricultural Machinery, 2023, 54(2):419-429,440.(in Chinese)
[19] LI Bing, CHEN Yuan, DENG Zongquan, et al. Conceptual design and analysis of the 2T1R mechanism for a cooking robot[J]. Robotics and Autonomous Systerms,2011,59(2):74-83.
[20] 沈惠平,朱忠颀,孟庆梅,等.零耦合度空间2T1R并联机构运动学与刚度建模分析[J]. 农业机械学报,2020,51(10):411-420. SHEN Huiping, ZHU Zhongqi, MENG Qingmei, et al. Kinematics and stiffness modeling analysis of spatial 2T1R parallel mechanism with zero coupling degree[J]. Transactions of the Chinese Society for Agricultural Machinery, 2020, 51(10):411-420.(in Chinese)
[21] 邹建星,罗玉峰,石志新,等.一种新型2T1R并联机构的位置与工作能力分析[J].机械设计与研究,2020,36(3):19-22,29.ZOU Jianxing, LUO Yufeng, SHI Zhixin, et al. Analysis of workspace and rotational capacity of 2-translational and 1-rotation parallel mechanism[J]. Machine Design and Research, 2020,36(3):19-22,29.(in Chinese)
[22] 李永泉,郭雨,张阳,等.基于牛顿欧拉法的一种空间被动过约束并联机构动力学建模方法[J].机械工程学报,2020,56(11):48-57.LI Yongquan, GUO Yu, ZHANG Yang, et al. Dynamic modeling method of spatial passive over-constrained parallel mechanism based on Newton Euler method[J]. Journal of Mechanical Engineering, 2020,56(11):48-57.(in Chinese)
[23] 高洪,赵韩.6-3-3并联机构逆动力学分析与仿真[J].农业机械学报,2007,38(9):130-133,111.GAO Hong, ZHAO Han. Inverse dynamic analysis and simulation of 6-3-3 parallel mechanism with six-degree-of-freedom[J]. Transactions of the Chinese Society for Agricultural Machinery,2007,38(9):130-133,111.(in Chinese)
[24] 杨廷力,沈惠平,刘安心,等.机器人机构拓扑结构设计[M].北京:科学出版社,2012.
[25] 沈惠平.机器人机构拓扑特征运动学[M].北京: 高等教育出版社,2021.