0 引言
随着无人机(Unmanned aerial vehicle,UAV)技术的不断发展,多旋翼无人机已经成为无人机领域中的重要一员。然而,多旋翼无人机在飞行过程中会受到各种外部扰动的影响,如气流扰动、风速扰动、载荷变化等,这些扰动会对多旋翼无人机飞行控制系统的稳定性和控制精度产生不利影响,主要表现在风、湍流等方面,这些气流扰动会直接作用在无人机旋翼上,改变旋翼产生的升力大小和方向,从而影响无人机姿态和位置控制,严重时甚至会导致无人机失控坠毁。在受到外部扰动时,无人机动态行为可能会发生急剧变化,传统的线性控制方法往往难以处理这种非线性控制问题;其次,由于外部扰动是实时变化的,无人机控制系统需要具备快速响应的能力,及时调整飞行策略和控制指令,以保证飞行稳定性和安全性。为了解决以上技术难点,自抗扰控制技术被引入到多旋翼无人机的控制系统中。自抗扰控制技术可以通过扰动观测器和补偿器来实现对扰动的实时监测和补偿,从而提高控制系统鲁棒性和稳定性[1-2]。因此,如何实现多旋翼无人机的自抗扰控制,提高其自适应性和抗扰性,成为当前无人机领域的研究热点之一。
在多旋翼无人机自抗扰控制技术方面,国内外学者们做了很多研究[3-14]。李晓东等[15]提出了一种基于自适应滑模控制和扰动观测器的多旋翼无人机控制方法,该方法可以实现对多种扰动的实时监测和补偿,提高了多旋翼无人机鲁棒性和稳定性。武晓晶等[16]也提出了一种基于自适应控制和扰动观测器的多旋翼无人机控制方法,该方法可以实现对风速扰动和载荷变化等扰动的实时监测和补偿,提高了多旋翼无人机自适应性和抗扰性。ALEXIS等[17]提出了一种基于模型预测控制的多旋翼无人机控制方法,该方法可以实现对多种扰动的实时监测和补偿,提高了多旋翼无人机鲁棒性和稳定性。HERBERT等[18]提出了一种基于深度学习的多旋翼无人机控制方法,该方法可以实现对多种扰动的实时监测和补偿,提高了多旋翼无人机自适应性和抗扰性。钟元等[19]提出了一种基于串级线性自抗扰控制的四旋翼无人机控制方法,有风干扰下该控制器具有较好的鲁棒性,能够运用到各种类型旋翼无人机工程控制中。焦环宇等[20]针对外界干扰设计了一种改进串级自抗扰控制方法,提高了无人机抗干扰能力和动态特性。
综上所述,多旋翼无人机自抗扰控制技术是当前研究热点,其应用前景广阔。然而,多数研究工作依然存在不足:参数数量多,参数整定复杂;采用降阶线性自抗扰控制器提高了估计进度,降低了噪声影响,但没有解决带宽与扰动跟踪速度的矛盾;将自抗扰算法与自适应控制、深度学习、模糊控制等智能算法相结合,提升了动态性能及参数整定效果,但是算法复杂,工程应用困难。本文对多旋翼无人机自抗扰控制技术进行优化,引入更精确的动力学模型,改进扰动观测速度,降低扩张状态观测器(Extended state observer,ESO)的阶数,以降低系统参数复杂性和算法实现计算难度,提升控制器调参简易性、飞行稳定性和安全性。此外,本文设计的ESO是模型辅助的,能够获取对象的部分信息,将这些已知的部分信息加入到ESO中,以降低观测器负担(带宽),或者在不降低带宽的情况下提高扰动估计精度,以提高控制效果。并将其应用于八旋翼无人机系统,以提升其针对非线性、强耦合、重量和转动惯量等不确定性影响的抗干扰能力,以期为多旋翼无人机的控制和应用提供参考。
1 多旋翼无人机系统动态模型
根据牛顿-欧拉动力学方程[21]和刚体运动定理[22],建立八旋翼无人机动态模型,主要包括描述基于牛顿第二定律的飞机加速度、角加速度与飞机受到的合力、合力矩关系的动力学模型,以及描述飞机姿态、角速度等运动学模型。设机体升力合力为u1,机体3个方向合力矩为u2、u3、u4,机体质量为m,重力加速度为g,则多旋翼无人机系统运动学与动力学模型可表示为
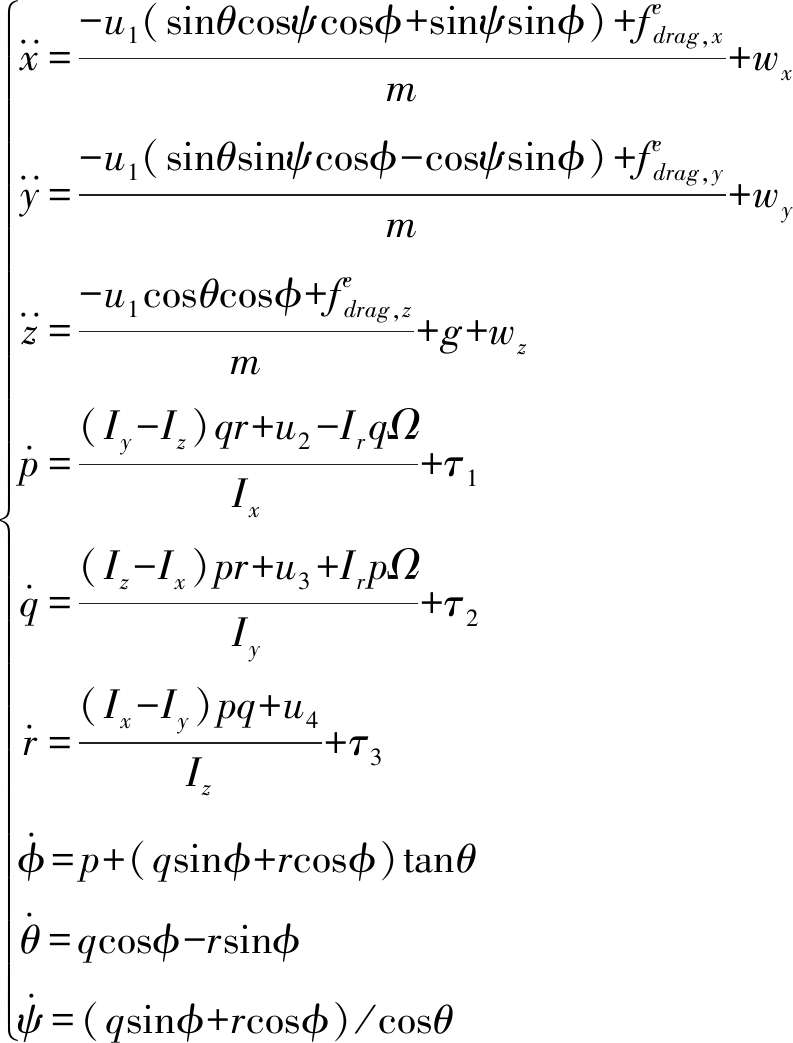
(1)
其中![]()
(2)
式中 ![]() 北东地线运动3个方向加速度
北东地线运动3个方向加速度
![]() 机体坐标系3轴角加速度
机体坐标系3轴角加速度
![]() 无人机机体3轴角速度
无人机机体3轴角速度
φ、θ、ψ——无人机的机体3轴姿态角
Ix、Iy、Iz——机体坐标系下3轴转动惯量
Ir——电机转动惯量
w、τ——系统内部和外部总的扰动
![]() 气动阻力
气动阻力
Ω——扭矩不平衡系数
ωk——第k个电机转速
控制分配时需采取机体坐标系的力和力矩平衡方程数学模型。由于本文八旋翼无人机的电机安装存在倾斜角,所以需将地理坐标系下3轴升力分量(北东地NED)转换到机体坐标系下3轴升力分量(前右下XYZ),便于后续的控制分配。
由欧拉角法或四元数法可知,地理坐标系到机体坐标系旋转矩阵为
![]()
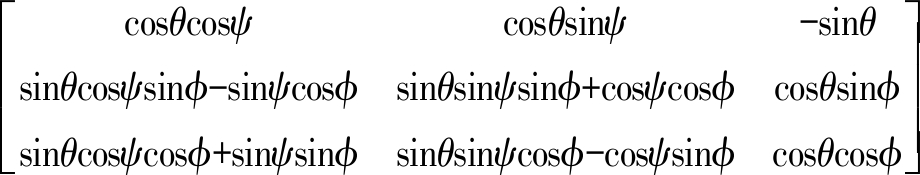
(3)
则重力向量旋转到机体坐标系旋转矩阵为
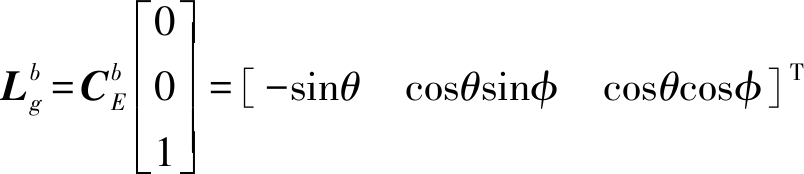
(4)
机体坐标系u1 3轴分量为
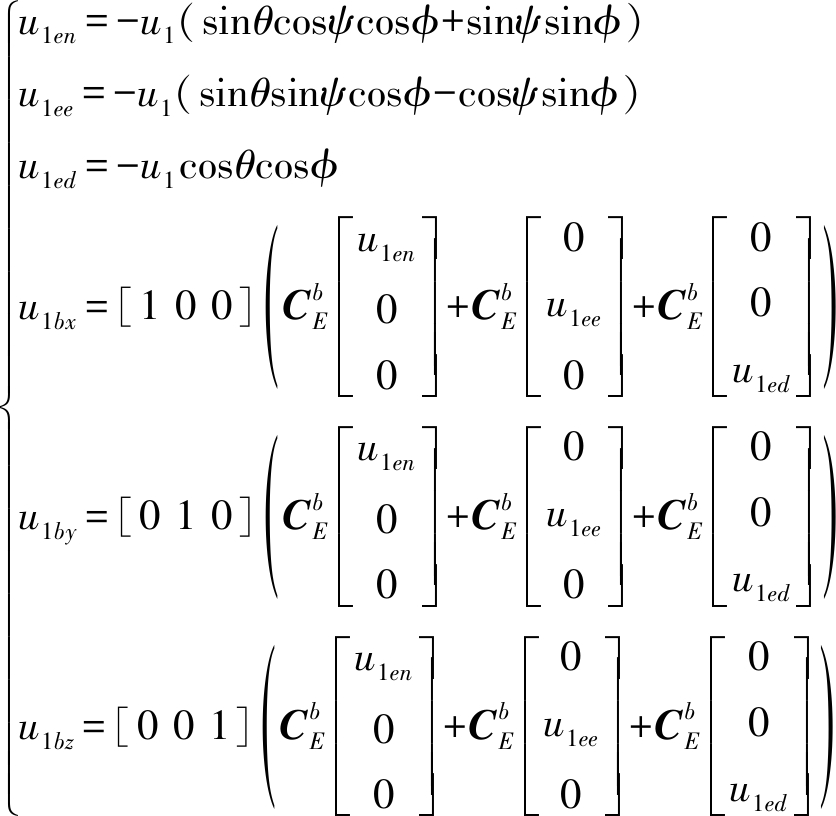
(5)
式中 u1en、u1ee、u1ed——升力在地理坐标系北东地3方向分量
u1bx、u1by、u1bz——升力在机体坐标系3轴分量
定义重力G在机体坐标系下3轴分量为
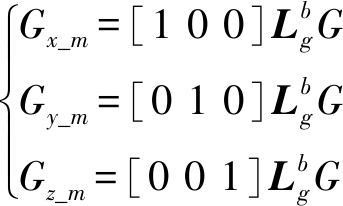
(6)
则六自由度力和力矩平衡方程表示为

(7)
式中,T和M为控制分配系数矩阵A中的元素,lz为重心在Z轴上的偏差。
2 自抗扰控制基本原理
自抗扰控制技术的核心是把系统未建模动态扰动和位置外扰动作用都归结为对系统的“总扰动”而进行估计并给予补偿。自抗扰控制器结构如图1所示,主要包括3个关键部分:跟踪微分器、扩张状态观测器和误差反馈控制器(非线性组合控制器)。
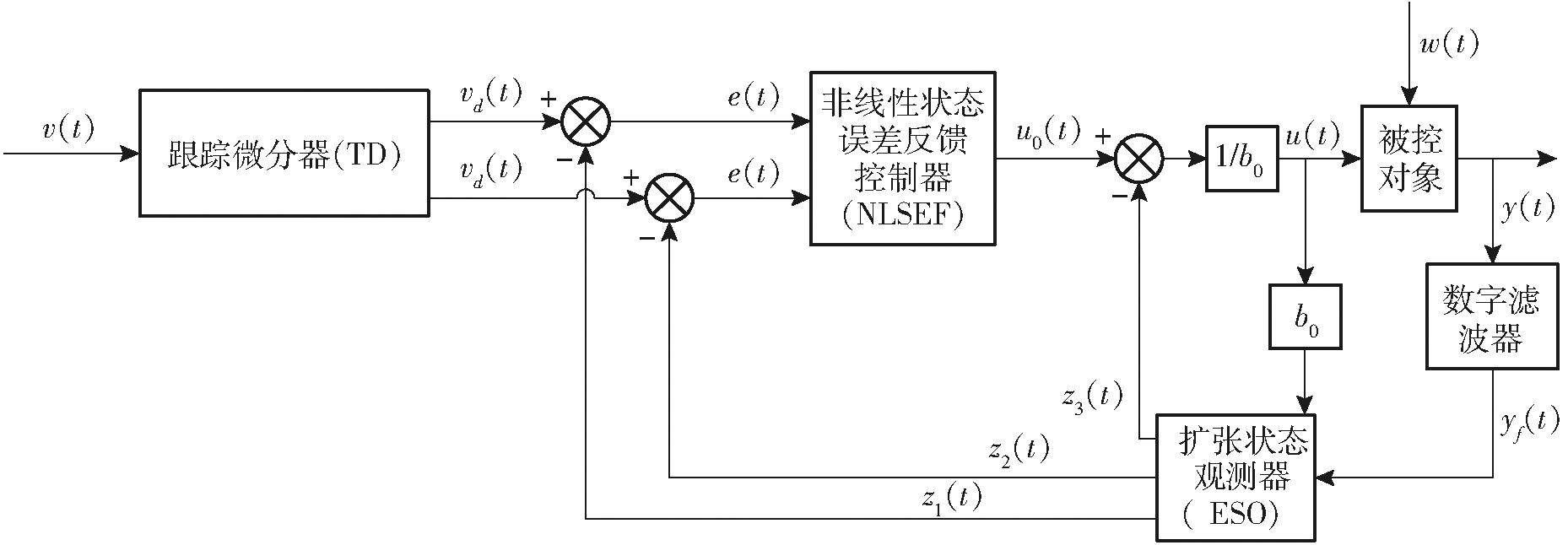
图1 自抗扰控制器结构图
Fig.1 Structural diagram of self disturbance rejection controller
跟踪微分器的作用是对输入信号事先安排过渡过程,提取含有随机噪声的输入信号及其微分信号,可以降低初始误差,且能够剔除杂波抑制噪声,得到光滑的输入信号,解决PID超调和快速性之间的矛盾[23-25]。扩张状态观测器可以估计系统内外扰动的实时作用值,并在反馈中给予补偿,用补偿的方法消除扰动的影响,从而具有抗干扰的作用。
误差反馈控制器主要对扰动进行抑制,根据跟踪微分器给定的信号及其微分,与扩张状态观测器得到的系统状态及其导数计算误差,利用非线性组合的方法计算控制量,补偿扰动。
被控对象为
(8)
式中 ![]() 系统的已知标称模型
系统的已知标称模型
fd——综合了系统内外扰动的总扰动
b——补偿因子
u——控制系统向被控对象的输出
令![]() 则式(8)转换为
则式(8)转换为
(9)
2.1 跟踪微分器
设v1为跟踪信号。线性跟踪微分器为
(10)
其中,R>0决定了跟踪速度,故称其为速度因子。
将上述线性跟踪微分器离散化,得到
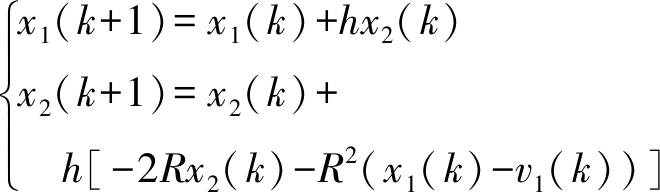
(11)
式中 h——采样周期
k——当前时刻
非线性跟踪微分器为
(12)
式中 r0——速度因子 h0——滤波因子
如图2所示,r0越大跟踪越快,但同时当v1中含有杂波或噪声时,跟踪信号越容易受噪声污染,滤波效果会降低,所以r0一般不能取太大;h0对信号的噪声起滤波作用,一般取h0=h,也可以取采样周期的整数倍,过大时会使跟随滞后。fhan为一种最速控制综合函数,其作用为较好地安排参考信号的过渡过程,使之不发生超调。具体形式为
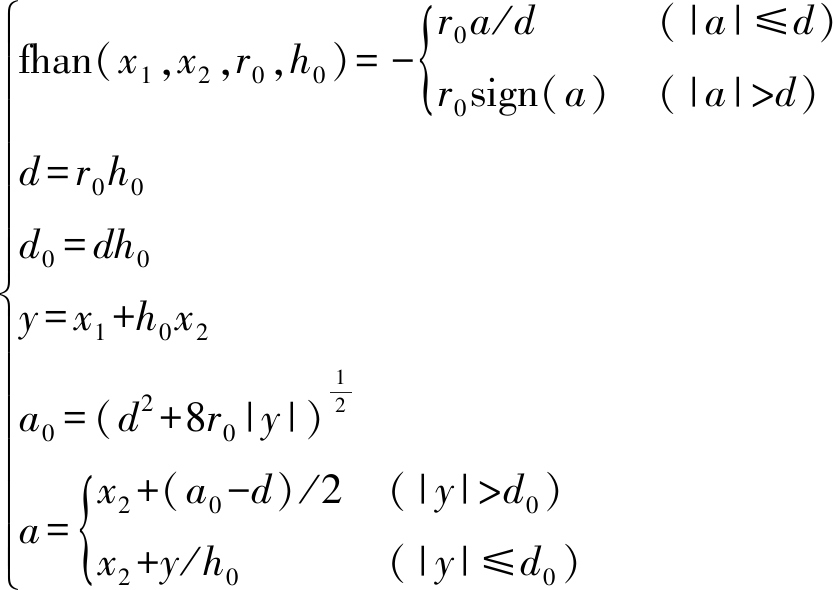
(13)
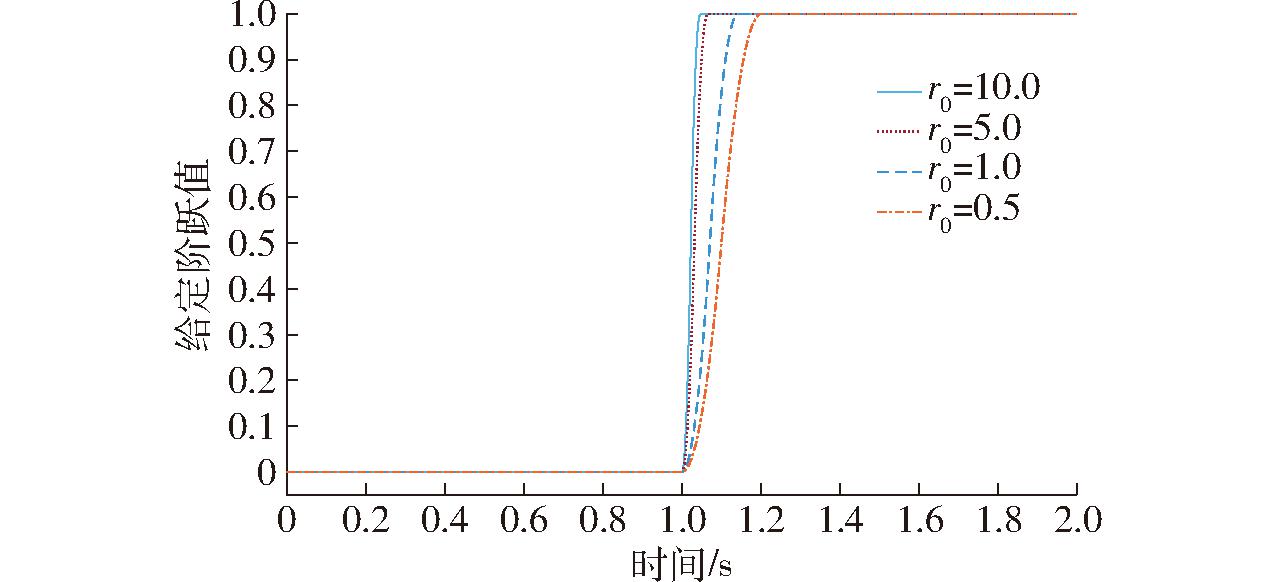
图2 二阶线性跟踪微分器阶跃响应曲线
Fig.2 Step response of second-order linear
tracking differentiator
式中 a0——响应速度调节参数
a——噪声抑制调节参数
对应的离散算法为
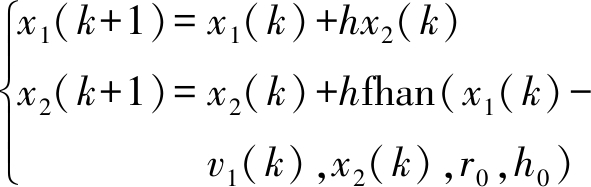
(14)
2.2 估计状态和总扰动
2.2.1 无法测量速度/角速度y2
扩张状态观测器设计为
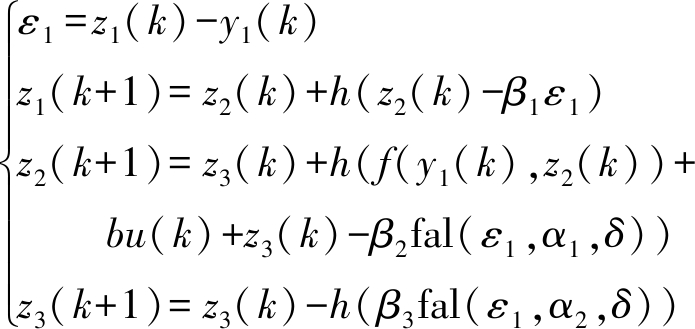
(15)
式中 z1——系统输出y1观测值
z2——系统输出y2观测值
z3——系统总扰动观测值
ε1——观测误差
δ——非线性调节阈值
β1、β2、β3、α1、α2——控制器可调参数
fal——噪声滤波器非线性函数
一般取β1=1/h,β2=1/h2,β3=1/h3,α1,α2∈(0,1)。β1在一定范围内调节无影响,但超出某一阈值后输出会振荡。β2有微分环节的作用,因为是负值,越小其微分效果越强,能够减小超调但会影响响应速度。β3可以减小超调,越大超调越大,但大于某一阈值时会造成振荡。fal定义为
(16)
fal函数是一种特殊的非线性结构,是自抗扰控制器中扩张状态观测器(ESO)的核心部分。基于fal函数的fal函数滤波器,对于噪声有较好的滤波效果,用于处理量测环节带有噪声干扰的情况。
2.2.2 可以测量速度/角速度y2
模型辅助的降阶状态观测器设计为
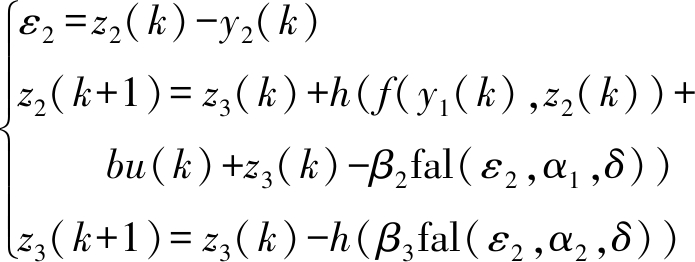
(17)
2.3 控制器设计
非线性误差反馈控制律是非线性PID组合控制,由于ESO能够实时估计并补偿外部与内部扰动,因此传统PID中在常值扰动下为消除静差而采用的积分器已不再必要,所以进一步简化为非线性PD组合控制。
对于无法测量速度/角速度y1,有
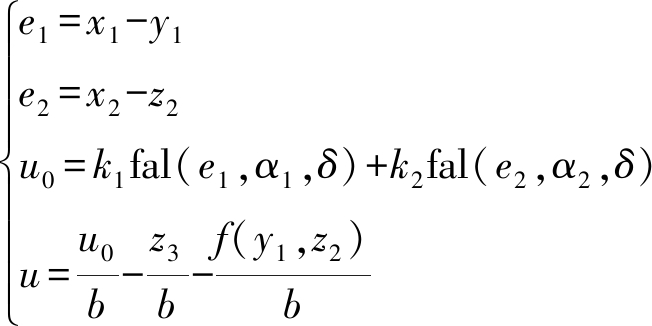
(18)
对于可以测量速度/角速度y2,有
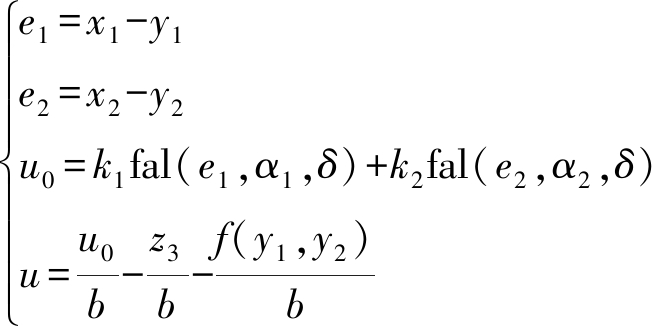
(19)
3 无人机控制器设计
通过前述对无人机动态模型的建立与分析,可以清晰地确定姿态角(滚转、俯仰和偏航)可以分别通过u2、u3、u4来控制,而位置(x,y,z)可以通过u1来控制。
3.1 位置控制
3.1.1 水平位置控制
定义
(20)
(21)
则多旋翼无人机位置动力学模型可表示为
(22)
设指令位置为![]() 则使用如下非线性跟踪微分器来跟踪lhc。
则使用如下非线性跟踪微分器来跟踪lhc。
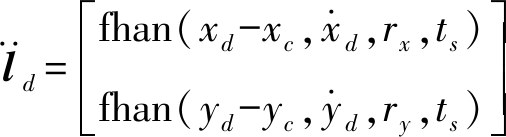
(23)
式中 l——无人机位置
ts——采样周期
状态观测器设计为
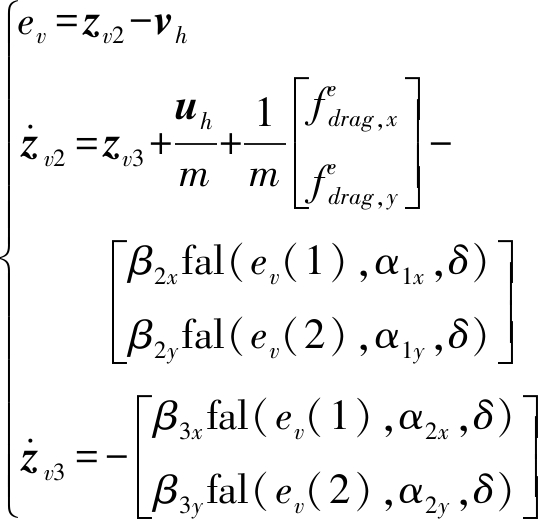
(24)
式中 zv2——位置输出微分观测值
zv3——位置总扰动观测值
β2x、β2y——二阶位置观测系数
β3x、β3y——三阶观测扰动系数
α1x、α1y、α2x、α2y——噪声滤波器可调参数
控制器设计为
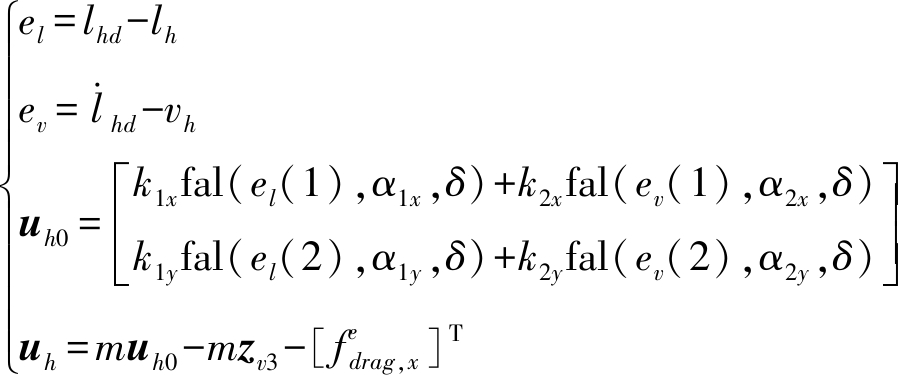
(25)
3.1.2 高度控制
用H表示高度,对多旋翼无人机位置动力学方程进一步处理可得
(26)
其中
使用非线性跟踪微分器
(27)
来跟踪Hc。
状态观测器设计为

(28)
控制器设计为
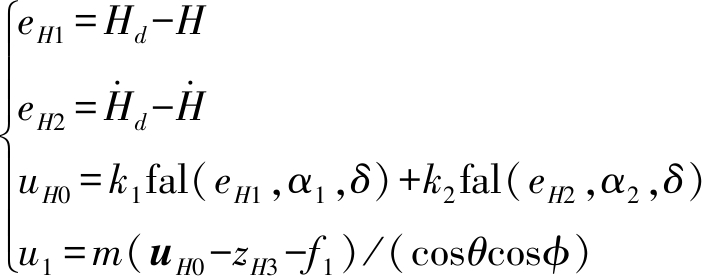
(29)
3.1.3 中间指令信号求解
由机体坐标系到大地坐标系的转换关系可以求解俯仰θc和滚转φc指令信号。
(30)
可得

(31)
又u1ed=-u1cosθccosφc,则有
(32)
可得
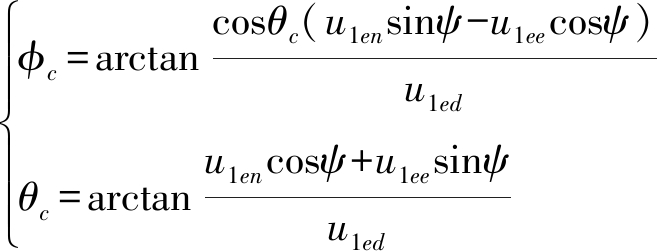
(33)
3.2 姿态控制
对多旋翼无人机姿态动力学方程进一步处理可得
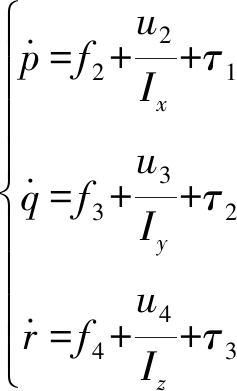
(34)
其中
f2=[(Iy-Iz)qr-IrqΩ]/Ix
f3=[(Iz-Ix)pr+IrpΩ]/Iy
f4=(Ix-Iy)pq/Iz
3.2.1 滚转角控制
使用非线性跟踪微分器来跟踪φc,即
(35)
状态观测器设计为
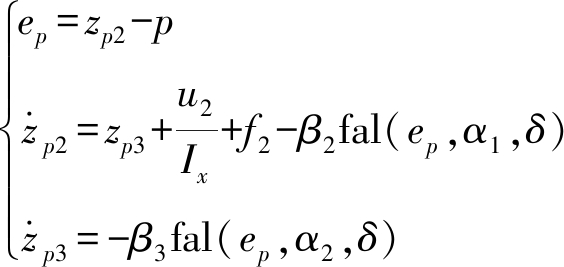
(36)
控制器设计为
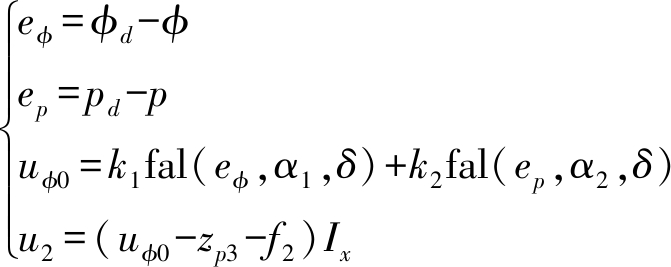
(37)
3.2.2 俯仰角控制
使用非线性跟踪微分器来跟踪ψc,即
(38)
状态观测器设计为
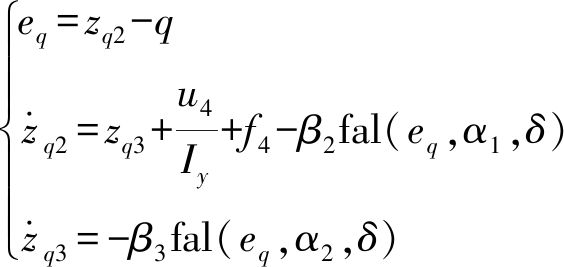
(39)
控制器设计为
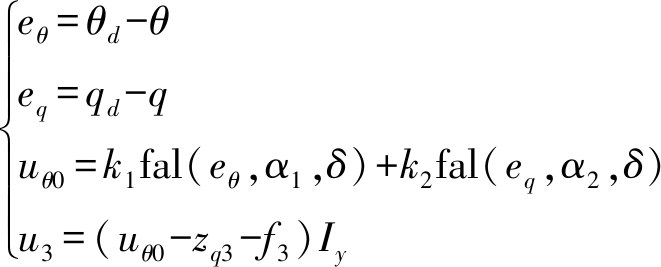
(40)
3.2.3 偏航角控制
使用非线性跟踪微分器来跟踪θc,即
(41)
状态观测器设计为
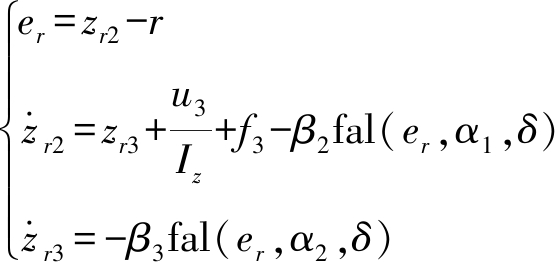
(42)
控制器设计为
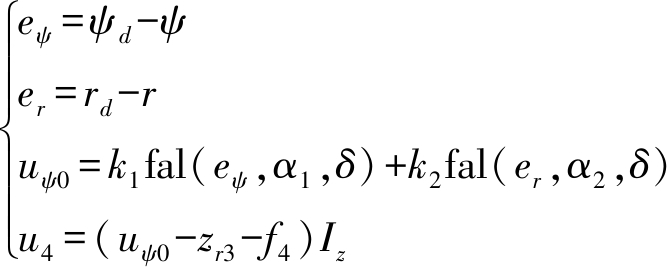
(43)
本文所设计的扩张状态观测器,除了对系统自身状态进行观测,同时对系统模型不确定性和系统外部扰动作为总扰动扩张为另一个状态,再通过控制器进行补偿。此外,利用扩张状态观测器估计的状态中既包含扰动信息,又包含系统输出及其1~n-1阶(n为原系统阶数)导数。通常情况下,系统输出可以直接获得,甚至某些低阶导数也可以通过一定的方式得到。这样,就没有必要再利用扩张状态观测器来估计这些状态变量,因而可以简化ESO结构,得到降阶的扩张状态观测器。由于可以直接通过传感器数据(Simulink仿真中通过六自由度模块计算得到)获取到角度/角速度,减少2个状态观测量,降低了系统参数复杂性和算法实现计算难度,提升了控制器调参简易性、飞行稳定性和安全性。
4 无人机控制分配模型
本文研究对象为有8个升力旋翼螺旋桨的复合翼无人机,其分布及编号如图3所示。
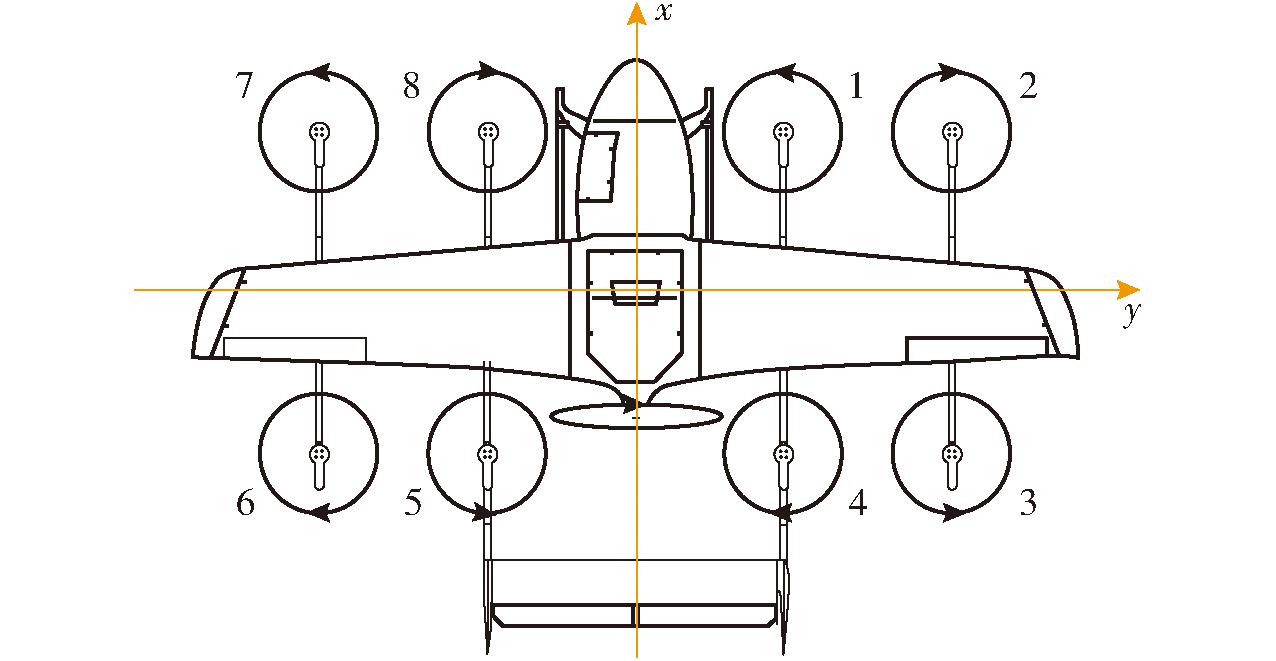
图3 无人机螺旋桨分布与编号示意图
Fig.3 Schematic distribution and numbering of UAV propeller
无人机控制分配模型主要描述包括飞机升力、阻力在内的飞机各执行器输出的力和力矩,与飞机受到的合力、合力矩之间的关系。
对飞行器电机螺旋桨倾斜角进行定义:设定参数ρ和σ来表示升力空间角,σ为升力在xy平面的投影与y轴正方向的夹角,ρ为升力与z轴正方向的夹角。根据此空间角定义,各个执行器升力合力在机体x方向的分力为
(44)
在机体y方向的分力为
(45)
在机体z方向的分力为
(46)
进行分配模型数学分析,可得机体坐标系下6个自由度的力和力矩平衡方程(忽略气动力和力矩)
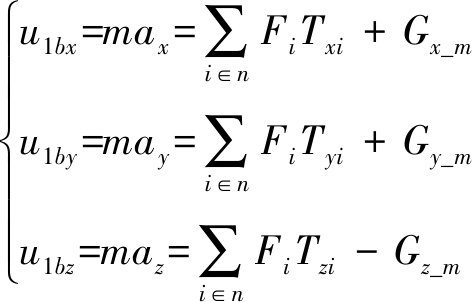
(47)
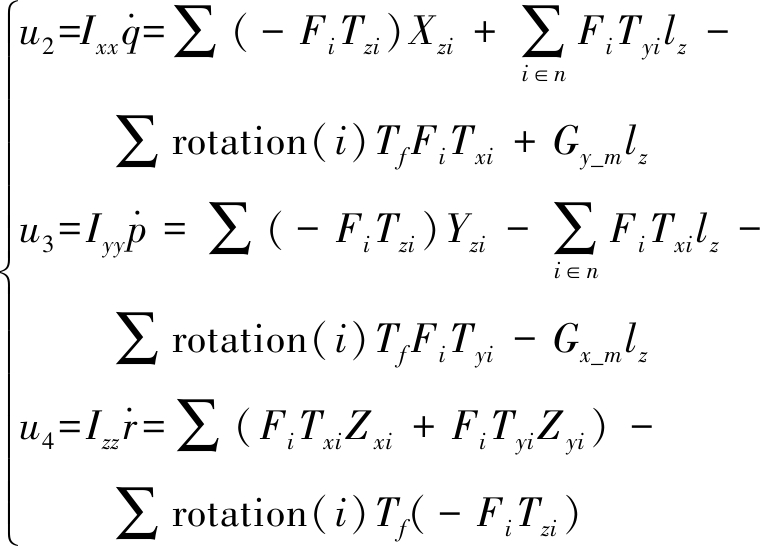
(48)
其中![]()
式中 Tf——扭矩拉力系数
由电机分布情况可知各轴方向上的力作用在3轴方向上的力矩的力臂矢量系数为
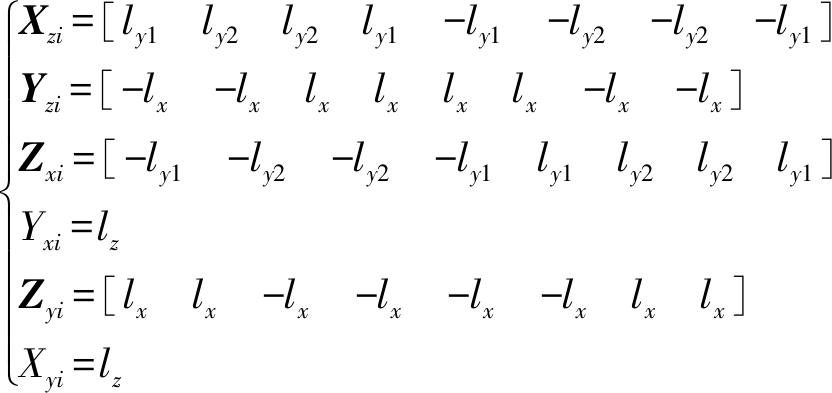
(49)
重力向量在机体的分量为
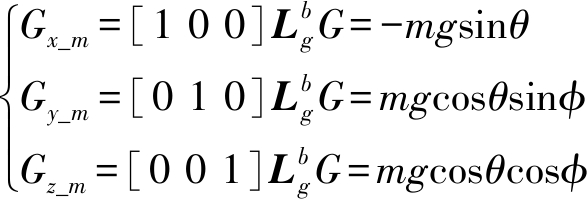
(50)
进而由第1节可知六自由度的力和力矩的平衡方程为

(51)
其中,由于u1求解时已经在北东天坐标系中平衡了重力,式(51)不必再出现机体三轴的重力分量项,但重心偏差产生的转矩还需保留。式中

(52)
求平衡方程总功率最小的控制分配解,可得

(53)
式中,A+1为控制分配系数矩阵的广义逆,此处由第1节机体坐标系u1的三轴分量,可知机体3个方向分力为
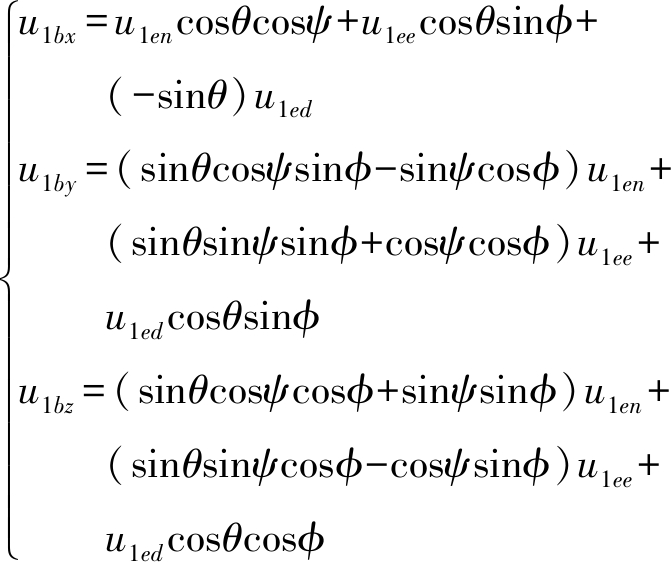
(54)
5 控制系统仿真
5.1 参数设置
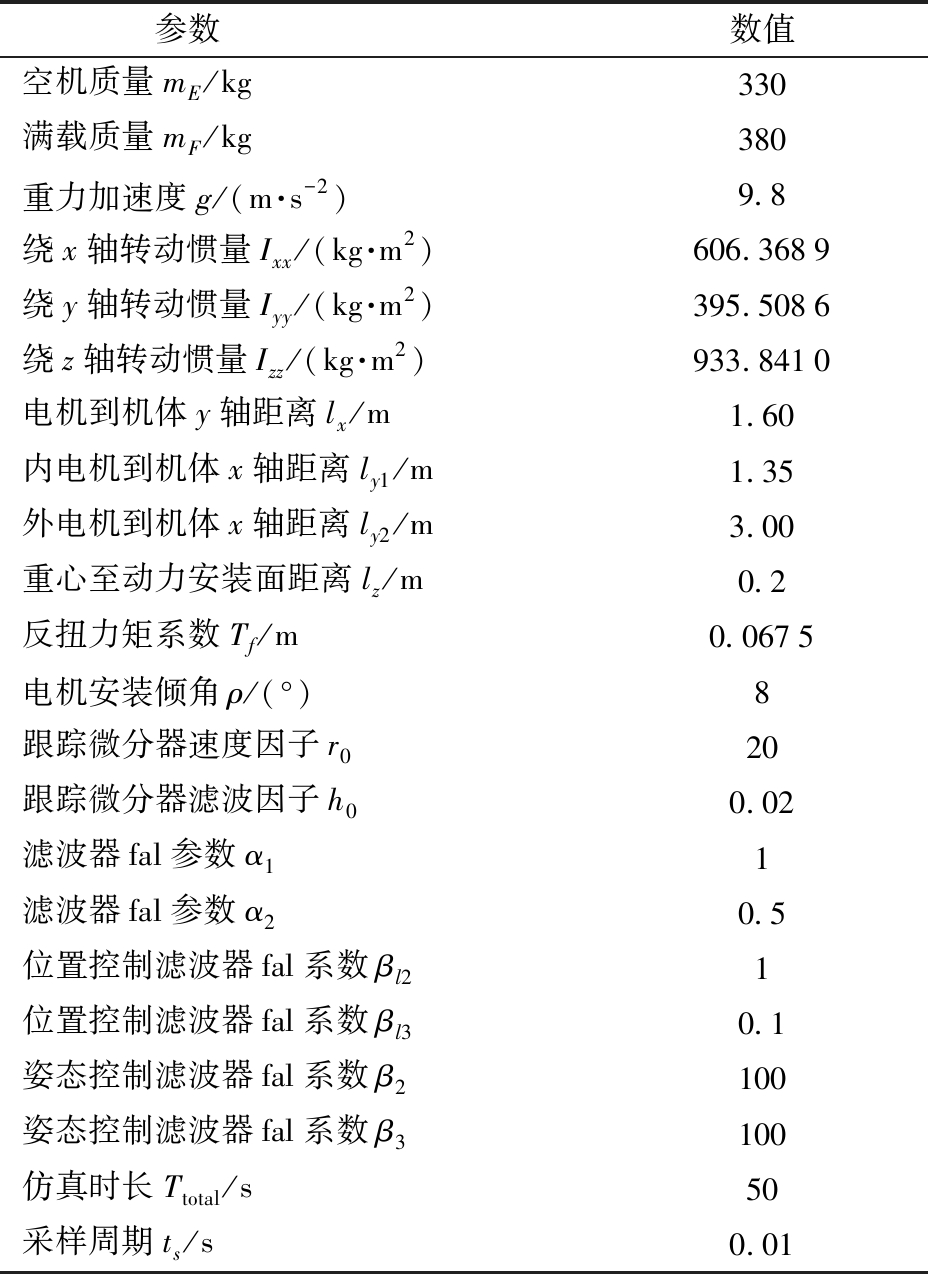
基于Matlab/Simulink环境搭建无人机模型,并根据前面所述的控制结构设计方法完成控制器和分配模型设计,使用风力模型模拟实际飞行中的风力扰动,同时模拟货物的重力扰动项,仿真研究无人机飞行姿态和位置控制效果,验证本文自抗扰算法的可靠性。仿真参数设置如表1所示。
表1 无人机模型与控制器参数
Tab.1 Parameters of UAV model and controller
参数数值空机质量mE/kg330满载质量mF/kg380重力加速度g/(m·s-2)9.8绕x轴转动惯量Ixx/(kg·m2)606.3689绕y轴转动惯量Iyy/(kg·m2)395.5086绕z轴转动惯量Izz/(kg·m2)933.8410电机到机体y轴距离lx/m1.60内电机到机体x轴距离ly1/m1.35外电机到机体x轴距离ly2/m3.00重心至动力安装面距离lz/m0.2反扭力矩系数Tf/m0.0675电机安装倾角ρ/(°)8跟踪微分器速度因子r020跟踪微分器滤波因子h00.02滤波器fal参数α11滤波器fal参数α20.5位置控制滤波器fal系数βl21位置控制滤波器fal系数βl30.1姿态控制滤波器fal系数β2100姿态控制滤波器fal系数β3100仿真时长Ttotal/s50采样周期ts/s0.01
5.2 仿真对比及分析
设定无人机北东地大地直角坐标系下初始位置为(0,0,0),飞行目标位置为(60 m,-80 m,100 m),飞至目标位置后悬停。
5.2.1 重力扰动仿真
控制模型中设定输入为空机质量,实际无人机模型中采用满载质量,相当于重力项扰动为50 kg货物,这对于自抗扰控制器是未知的不确定重力扰动项。有无重力扰动的仿真结果如图4、5所示。由仿真结果明显可知,无人机能够稳定地飞至目标位置,当存在重力项扰动时高度控制超调会稍大一点。但通过自抗扰控制器可以补偿不确定的重力扰动,无论有无重力扰动均能够实现良好的控制效果。
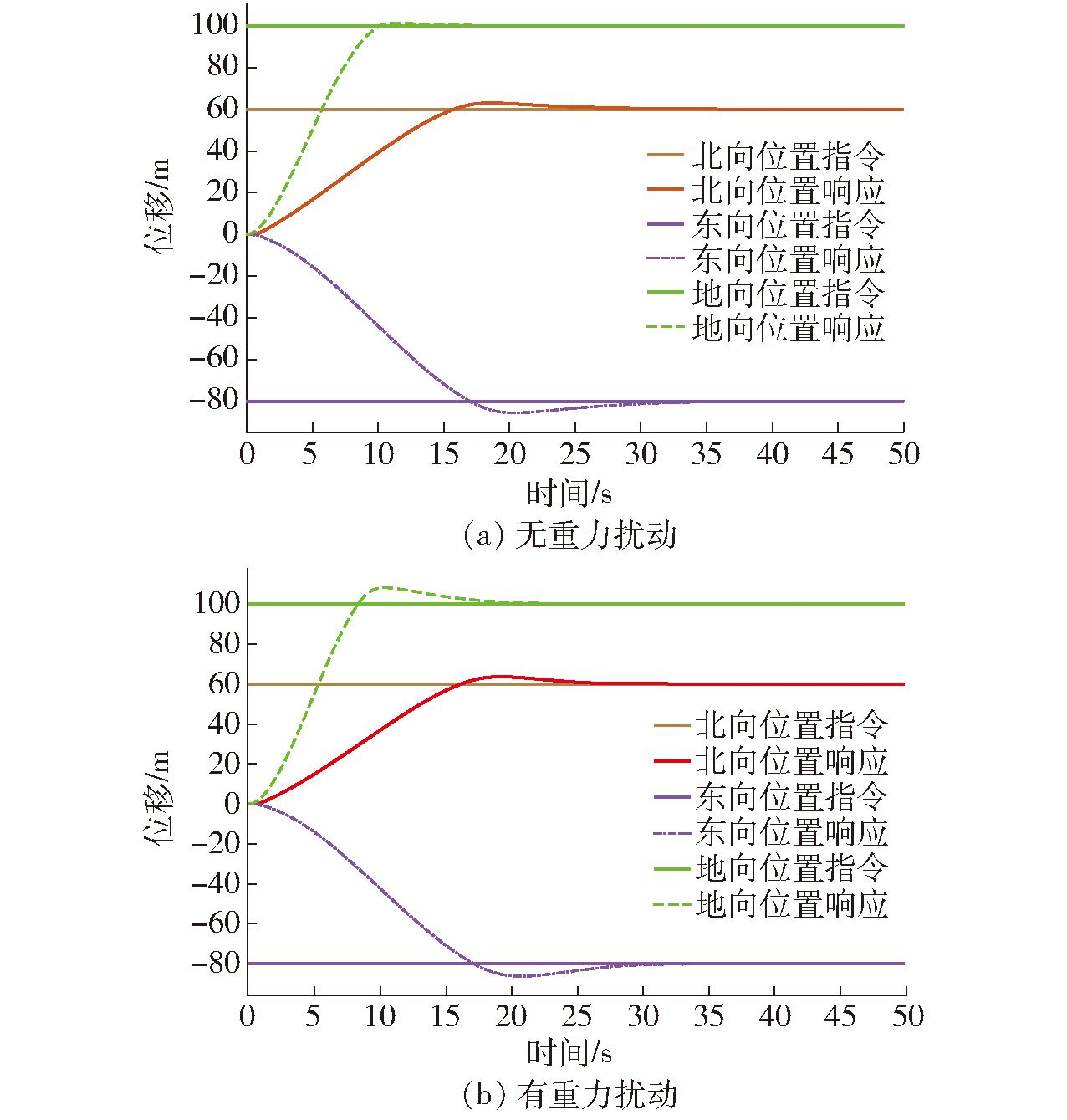
图4 位置响应仿真结果
Fig.4 Simulation results of position response
此外,由图5a可以看出,虽无明显的重力扰动,系统存在其他未知微弱扰动量;有重力扰动后,观测到的高度控制扰动从0.1 m/s2左右上升到1.4 m/s2,均已由本文设计的ESO观测器观测并最终补偿到控制器输出项。
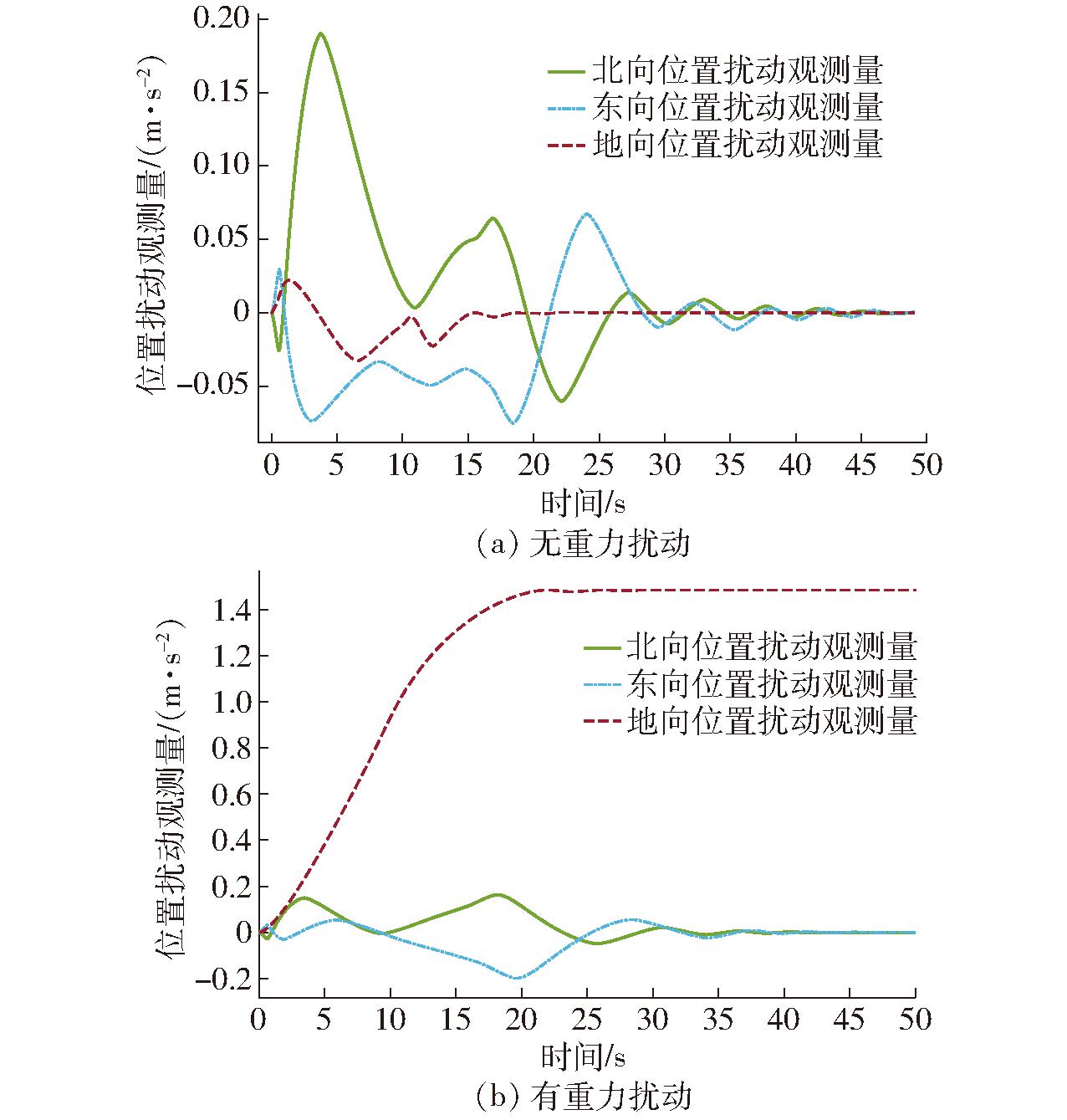
图5 位置控制扰动观测量变化曲线
Fig.5 Change curves of position control disturbance observation
有无重力扰动仿真的姿态响应结果没有区别,均如图6所示,姿态跟踪效果良好,且最终平稳悬停。为方便对比,均展示已添加重力扰动项后的仿真试验结果。

图6 姿态响应仿真结果
Fig.6 Simulation results of attitude response
通过观察上述位置响应和姿态响应的仿真结果,可以发现有无重力扰动,算法对位置控制精度和姿态保持精度均较高,姿态角误差整个过程控制在±0.12°以内,从而验证了系统稳定性。
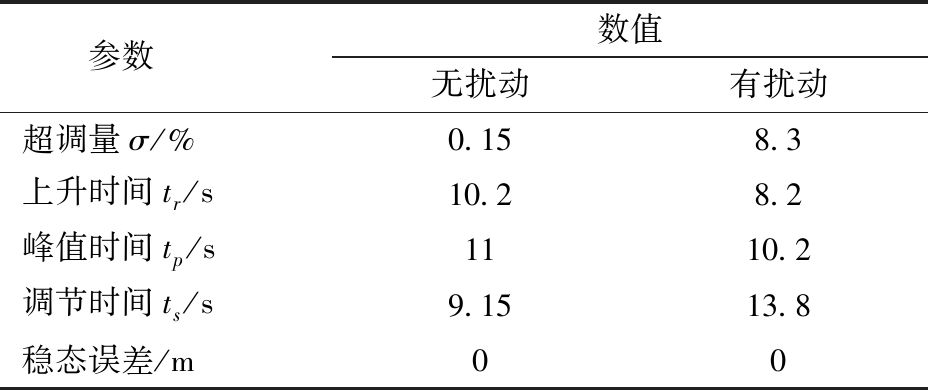
分析对比控制结果在加入重力扰动前后的动态性能,由图4~6可以看出重力扰动对高度控制效果影响较大,水平位置控制暂时不做统计。高度控制的快速性和稳定性分析指标统计结果见表2,可以看出有扰动后虽然超调量和调节时间相对大了一些,但上升时间和峰值时间并未增加甚至比无扰动时更快,较短的上升时间意味着系统能够更快地响应输入信号,从而更快地调整无人机的姿态、位置或速度。这对于提高无人机的操控性、响应速度和整体性能至关重要。说明选取合适,同时验证了系统的快速性。
表2 重力扰动仿真控制动态性能
Tab.2 Dynamic performance of gravity disturbance simulation control
参数数值无扰动有扰动超调量σ/%0.158.3上升时间tr/s10.28.2峰值时间tp/s1110.2调节时间ts/s9.1513.8稳态误差/m00
虽然本文为提升控制器调参简易性,控制器并未采用ESO的状态1和状态2(位置和速度均通过无人机模型反馈得到),仅采用ESO观测的系统未知扰动。但也对位置控制微分项进行了观测,通过分析图7~9可知,位置输出的微分观测量能够大致跟踪模型反馈的速度分量,观测误差在±0.5 m/s范围内,进一步验证了在系统存在不确定性扰动下,本文设计的扩张状态观测器ESO的可靠性。
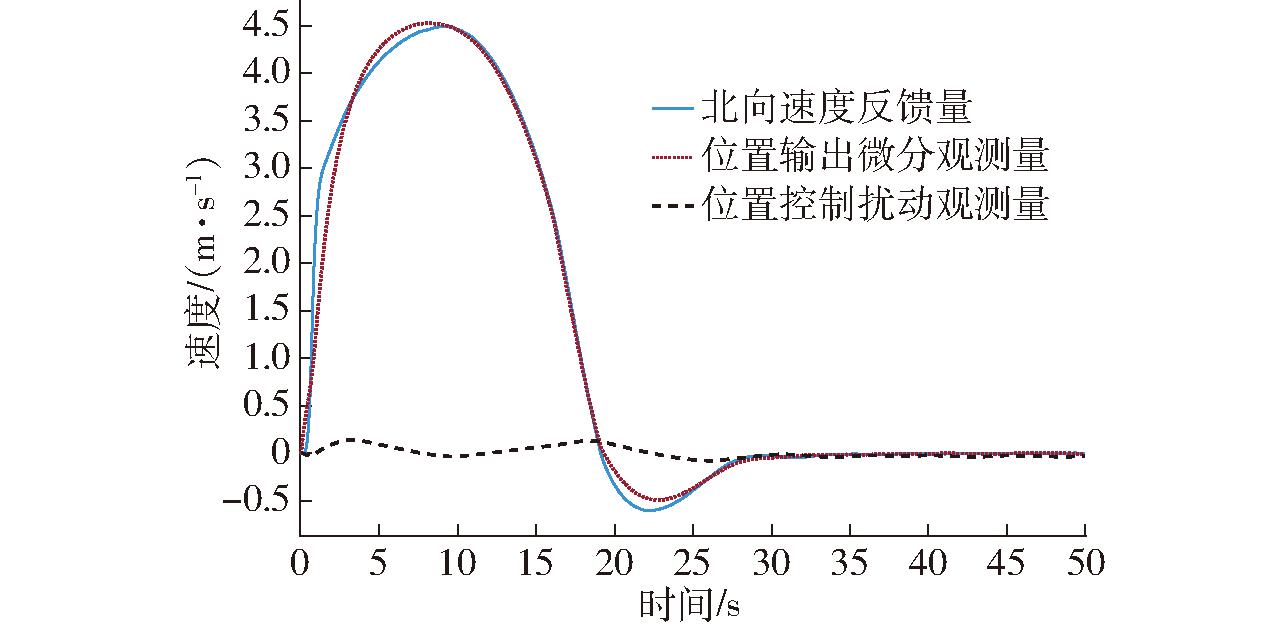
图7 北向速度观测器效果
Fig.7 Northward velocity observer effect
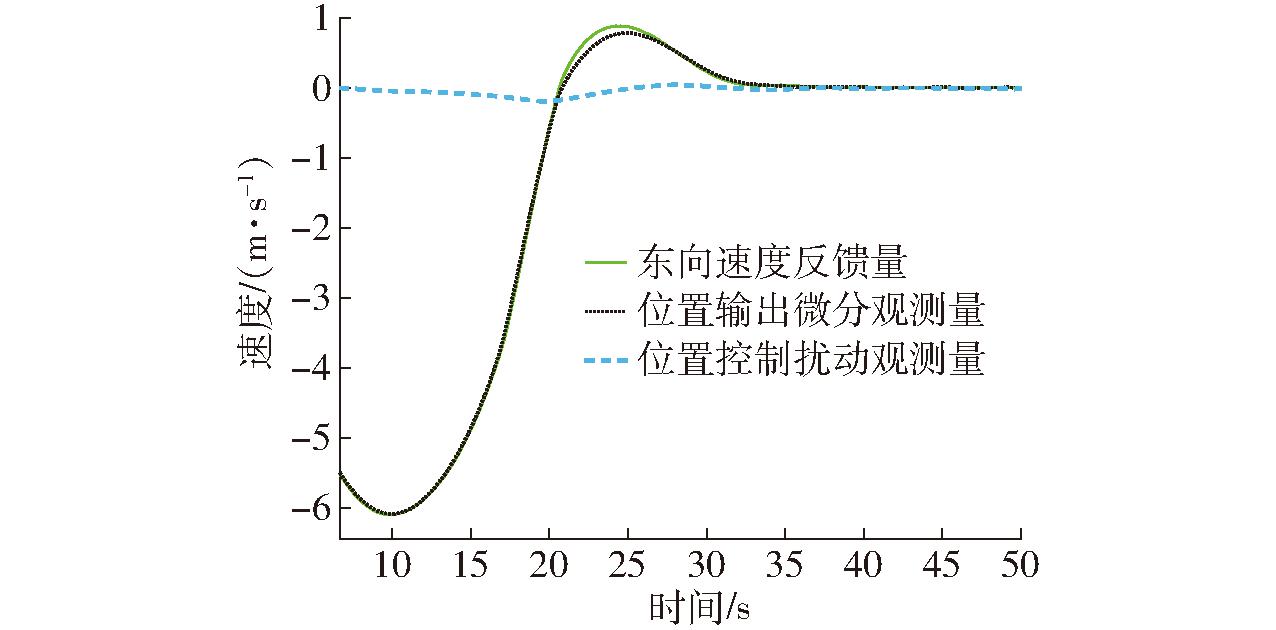
图8 东向速度观测器效果
Fig.8 Eastward velocity observer effect
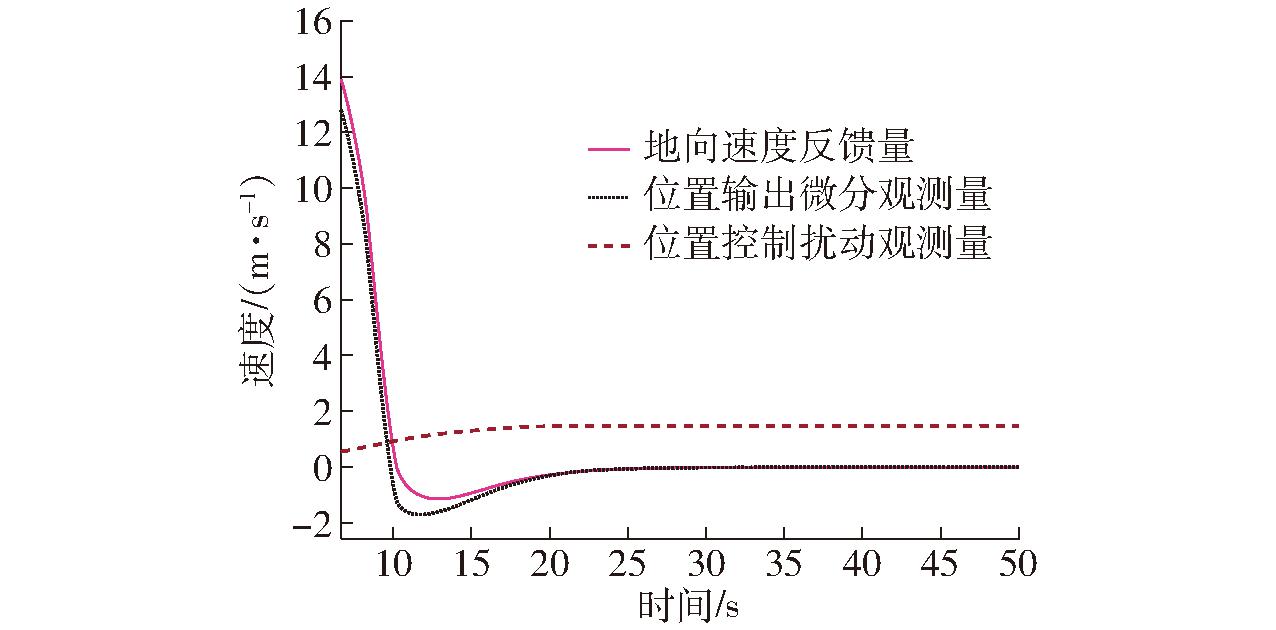
图9 地向速度观测器效果
Fig.9 Downward velocity observer effect
5.2.2 加风扰动仿真
给定常值风速为vw=3i+2j+0.2k。在常值风基础上叠加较强的带限白噪声的随机阵风,仿真对比常值风扰动和阵风扰动的控制效果。北东地3个方向的常值风和带噪阵风加在无人机机体上的效果如图10所示。
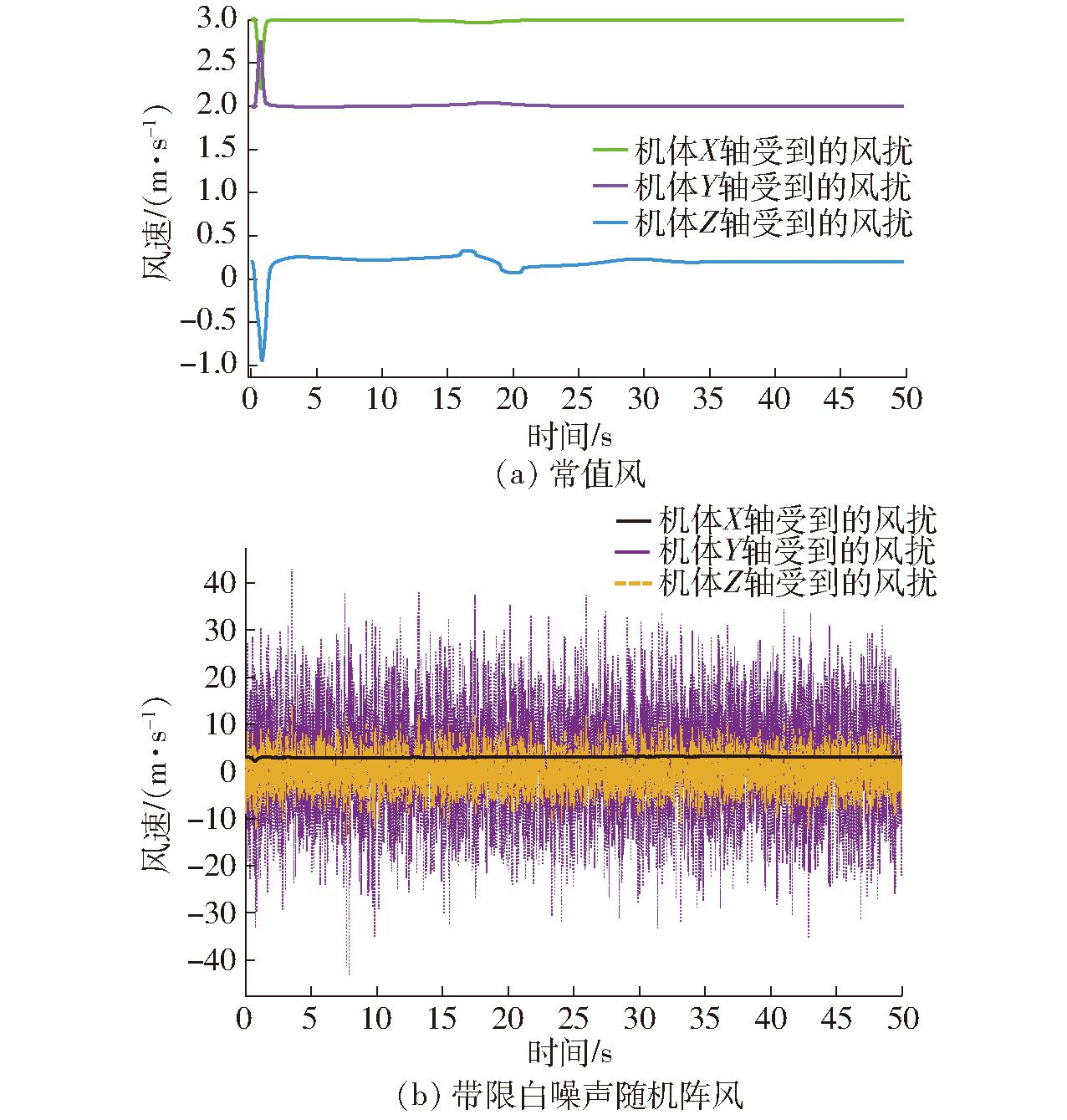
图10 机体受到的风力扰动变化曲线
Fig.10 Wind disturbance variation curves of body
位置响应在加入2种风扰后均未发生变化,依旧如图4所示。此外,针对常值风和阵风有区别的是控制器输出u1和8个螺旋桨的控制分配,以及姿态响应,仿真结果分别如图11和图12所示,这一点在35 s稳定悬停后表现尤为明显。这是由于所加阵风相对常值风变化剧烈(按采样周期设定随机白噪声)且强度较高,系统给定控制输出会根据随机阵风扰动响应迅速,每个执行器输出的力不再像对抗常值风一样为一个定值470 N,而是不断调整姿态以相应的快速变化进一步抵抗风扰,且不会产生较大的姿态角度,姿态控制稳态误差在0.05°以内。从而验证了系统针对外部扰动实时剧烈变化,可以实现非线性控制,并快速响应及时调整飞行控制输出指令的能力。
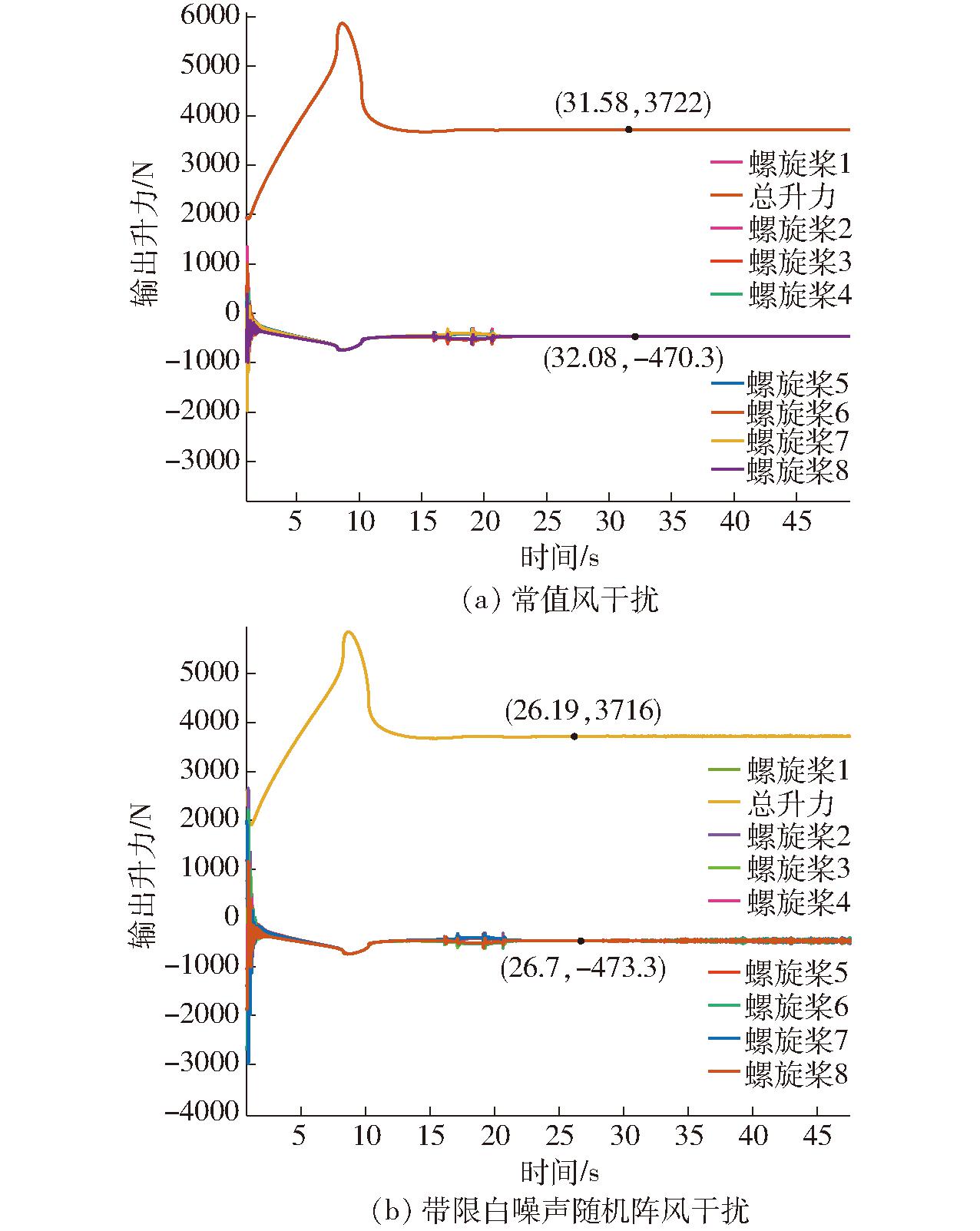
图11 各执行器输出升力(向下为正)与控制器输出机体升力合力(-u1为正值)
Fig.11 Output lift of each actuator (positive downward) and combined lift of controller output body lift (-u1 was positive)
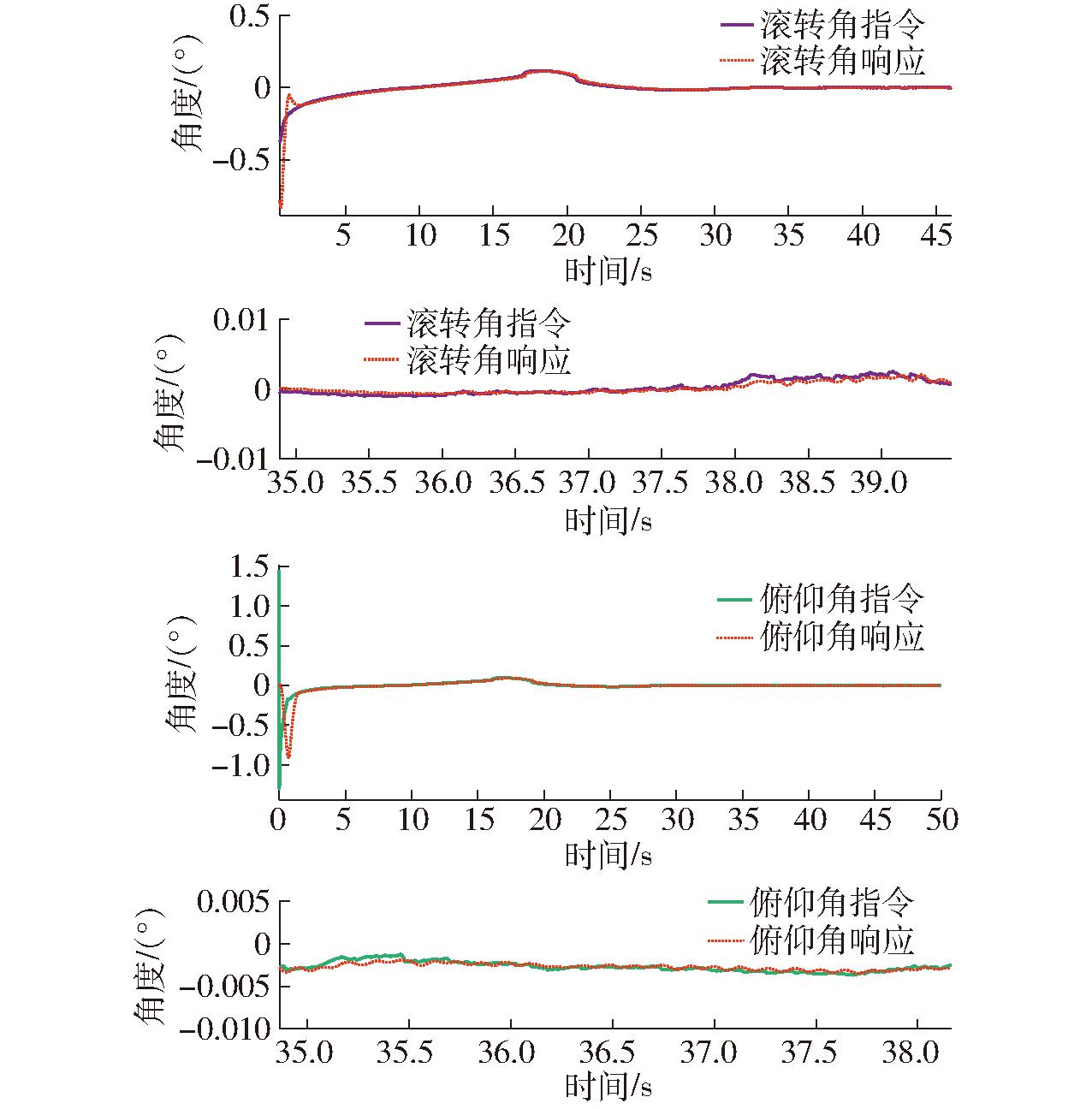
图12 带噪随机阵风下姿态响应
Fig.12 Attitude response under noisy random gusts
由图11还可以看出,无论控制器给定的重力是否与实际完全匹配,最终输出的升力都能自适应地平衡实际无人机的重力,验证了本文算法对不确定性扰动具有自适应能力。
综上,无论增加重力扰动(模型内部扰动)或者风扰(外力扰动),无人机都能够从初始点快速且平稳到达目标位置,并保持稳定悬停,从而验证了本文控制器的抗扰能力以及控制系统设计的准确性和可靠性。
6 结论
(1)建立了多旋翼无人机系统动态模型,设计了基于ADRC的位置和姿态控制器,解决了无人机受到外部扰动时动态行为发生急剧变化的非线性控制问题,提升了系统在扰动实时变化时控制系统快速响应的能力,可以及时调整飞行策略和控制指令,保证了飞行稳定性和安全性。
(2)以复合翼无人机的旋翼控制系统为研究对象,搭建了控制分配模型,通过仿真试验进行了验证。仿真试验中,给控制目标分别加入了不确定负载和风的干扰,仿真结果表明本文设计的控制器不仅可以很好地估计出系统内外扰动并进行补偿,而且具有极强的抗干扰性,满足了八旋翼无人机的控制要求。
(3)综合仿真试验结果,验证了本文所设计的控制系统可以稳定地控制飞行位置与姿态,平滑且快速地完成位置跟踪和稳定悬停,且跟踪精度高。同时,也验证了本文模型与算法的有效性。
[1] HAN J Q. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906.
[2] 马幼捷, 刘增高, 周雪松, 等. 自抗扰控制器的原理解析[J]. 天津理工大学学报, 2008, 24(4): 27-30.MA Youjie, LIU Zenggao, ZHOU Xuesong, et al. Analysis on principle of ADRC[J]. Journal of Tianjin University of Technology, 2008, 24(4): 27-30. (in Chinese)
[3] 徐雪松, 吴仪政, 倪赟. 变载荷四旋翼无人机的自适应模糊自抗扰控制[J]. 传感器与微系统, 2022, 41(7): 101-109.XU Xuesong, WU Yizheng, NI Yun. Adaptive fuzzy auto disturbance rejection control of variable load quadrotor UAV[J]. Transducer and Microsystem Technologies, 2022, 41(7): 101-109. (in Chinese)
[4] 任开众, 徐胜, 苏成悦, 等. 一种多旋翼无人机自抗扰姿态控制器[J]. 现代计算机, 2022, 28(8): 93-99.REN Kaizhong, XU Sheng, SU Chengyue, et al. An auto-disturbance-rejection attitude controller for multi-rotor unmanned aerial vehicle[J]. Modern Computer, 2022, 28(8): 93-99. (in Chinese)
[5] 朱文杰, 徐胜, 苏成悦. 多旋翼飞行器单参数自抗扰姿态控制器[J]. 电光与控制, 2021, 28(7): 16-21, 47.ZHU Wenjie, XU Sheng, SU Chengyue. Single-parameter active disturbance rejection attitude controller for multi-rotor aircraft[J]. Electronics Optics &Control, 2021, 28(7): 16-21, 47. (in Chinese)
[6] 石晓洁, 蔡家斌, 宋建, 等. 风干扰下无人机自抗扰控制参数自整定[J].组合机床与自动化加工技术, 2021(6): 67-71.SHI Xiaojie, CAI Jiabin, SONG Jian,et al. Self-tuning parameters of active disturbance rejection control for UAV under wind disturbance[J]. Modular Machine Tool &Automatic Manufacturing Technique, 2021(6): 67-71. (in Chinese)
[7] 石嘉, 裴忠才, 唐志勇, 等. 改进型自抗扰四旋翼无人机控制系统设计与实现[J]. 北京航空航天大学学报, 2021, 47(9): 1823-1831.SHI Jia, PEI Zhongcai, TANG Zhiyong, et al. Design and realization of an improved active disturbance rejection quadrotor UAV control system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2021, 47(9): 1823-1831. (in Chinese)
[8] 陈万考, 郭玉英. 基于极值搜索的四旋翼无人机自抗扰控制[J]. 飞行力学, 2021, 39(1): 54-61.CHEN Wankao, GUO Yuying. Extremum seeking based active disturbance rejection control for quadrotor UAV[J]. Flight Dynamics, 2021, 39(1): 54-61. (in Chinese)
[9] 吴君华, 谢习华, 李拥祺. 基于线性自抗扰控制技术的四旋翼无人机控制系统[J]. 传感器与微系统, 2021, 40(5): 102-110.WU Junhua, XIE Xihua, LI Yongqi. Four-rotor UAV control system based on LADRC technology[J]. Transducer and Microsystem Technologies, 2021, 40(5): 102-110. (in Chinese)
[10] 李一波, 胡杨, 陈伟, 等. 基于自抗扰控制技术的无人机编队控制器设计[J]. 飞行力学, 2015, 33(3): 205-208.LI Yibo, HU Yang, CHEN Wei, et al. Design of UAVs formation controller based on ADRC control technology[J]. Flight Dynamics, 2015, 33(3): 205-208. (in Chinese)
[11] 楼静梅, 张科. 基于自抗扰理论的无人机横侧向解耦控制研究[J]. 计算机测量与控制, 2014, 22(4): 1152-1154.LOU Jingmei, ZHANG Ke. Study on decoupling control of UAV lateral based on auto-disturbance-rejection control theory[J]. Computer Measurement &Control, 2014, 22(4): 1152-1154. (in Chinese)
[12] 张勇, 陈增强, 张兴会, 等. 双旋翼无人机串级线性自抗扰控制[J]. 中南大学学报(自然科学版), 2019, 50(3): 564-571.ZHANG Yong, CHEN Zengqiang, ZHANG Xinghui, et al. Attitude control of tandem rotor UAV based on cascade linear active disturbance rejection control[J]. Journal of Central South University (Science and Technology), 2019, 50(3): 564-571. (in Chinese)
[13] 韩文杰. 四旋翼无人机的自抗扰控制[D]. 哈尔滨:哈尔滨工业大学, 2019.HAN Wenjie. Active disturbance rejection control of quadcopter unmanned aerial vehicles[D]. Harbin: Harbin Institute of Technology, 2019. (in Chinese)
[14] 曹宇. 无人机非线性自抗扰控制方法研究[D]. 哈尔滨:哈尔滨工业大学, 2013.CAO Yu. Research of nonlinear active disturbance rejection control with applications to unmanned aerial vehicle[D]. Harbin: Harbin Institute of Technology, 2013. (in Chinese)
[15] 李晓东, 王宏伟. 基于自适应滑模控制和扰动观测器的多旋翼无人机控制[J]. 控制与决策, 2018, 33(10): 1915-1922.LI Xiaodong, WANG Hongwei. Multi rotor unmanned aerial vehicle control based on adaptive sliding mode control and disturbance observer[J]. Control and Decision, 2018, 33(10): 1915-1922. (in Chinese)
[16] 武晓晶,郑文棪,吴学礼,等. 基于扰动观测器的时变负载四旋翼无人机自适应有限时间控制[J]. 河北科技大学学报,2021,42(6):579-590.WU Xiaojing, ZHENG Wenyan, WU Xueli, et al. Adaptive finite-time control for quadrotor UAV with time-varying load based on distrubance observer[J]. Journal of Hebei University of Science and Technology, 2021, 42(6): 579-590. (in Chinese)
[17] ALEXIS K, PAPACHRISTOS C, NIKOLAKOPOULOS G, et al. Model predictive quadrotor indoor position control[C]∥Control &Automation IEEE, 2011.
[18] HERBERT S, WU J. Deep learning for robust control of UAVs subject to wind gusts[J]. IEEE Transactions on Control Systems Technology, 2019, 27(1): 33-45.
[19] 钟元, 章豪. 一种基于串级线性自抗扰控制的四旋翼无人机控制方法[J]. 航空电子技术, 2020, 51(1): 28-34.ZHONG Yuan, ZHANG Hao. A control method for quadrotor based on cascade linear active disturbances rejection controller[J]. Avionics Technology, 2020, 51(1): 28-34. (in Chinese)
[20] 焦环宇, 王春阳, 赵锦楠. 四旋翼无人机串级自抗扰控制及参数优化方法[J]. 理论与方法, 2021, 40(11): 35-40.JIAO Huanyu, WANG Chunyang, ZHAO Jinnan. Cascade active disturbance rejection control and parameter optimization method for quadrotor UAV[J]. Theory &Method, 2021, 40(11): 35-40. (in Chinese)
[21] 张婷. 基于ADRC的四旋翼飞行控制器设计[D]. 沈阳:东北大学, 2013.ZHANG Ting. Design of quadcopter flight controller based on ADRC[D]. Shenyang: Northeastern University,2013. (in Chinese)
[22] KLAUSEN K, FOSSEN T I, JOHANSEN T A. Nonlinear control with swing damping of a multirotor UAV with suspended load[J]. Journal of Intelligent &Robotic Systems, 2017, 88: 379-394.
[23] 王宇航. 基于ADRC的直接侧向力/气动力复合控制系统设计[D]. 哈尔滨:哈尔滨工业大学, 2009.WANG Yuhang. Design of lateral thrust and aerodynamics blended control system based on auto disturbance rejection controller[D]. Harbin: Harbin Institute of Technology, 2009. (in Chinese)
[24] 韩京清, 黄远灿. 二阶跟踪-微分器的频率特性[J]. 数学的实践与认识, 2003, 33(3): 71-74.HAN Jingqing, HUANG Yuancan. Frequency characteristic of second-order tracking-differentiator[J]. Mathematics in Practice and Theory, 2003, 33(3): 71-74. (in Chinese)
[25] 韩京清. 非线性跟踪微分器[J]. 系统科学与数学, 1994, 14(2): 177-183.HAN Jingqing. Nonlinear tracking-differentiator[J]. Journal of Systems Science and Mathematical Sciences, 1994, 14(2): 177-183. (in Chinese)