OSID：
三自由度的两平移一转动(2T1R)空间并联机构,因结构简单、控制方便,已在空间调姿、搬运、喷涂、误差补偿等领域应用。柳纪琛等[1]对2-PRR+PUS并联机构进行了运动学和奇异性分析,并利用粒子群优化算法对机构进行尺度优化设计;LI等[2] 基于Grassmann线几何和Atlas方法,提出了一种含闭环单元的2T1R和2R1T冗余驱动并联机构型综合方法,得到的机构具有良好的对称性和综合性能;这些机构无符号式位置正解,但具有部分运动解耦性。张彦斌等[3]提出了一种弱耦合的2T1R并联机构,得到了其位置正、逆符号解,并对机构进行了奇异性分析;LI等[4]给出了一类全铰链并且耦合度为零的1T1R和2T1R机构,并对其进行了运动学、动力学和奇异性分析; 沈惠平等[5]设计、分析了一种零耦合度且部分运动解耦的非对称两支链大转角2T1R并联机构,并对其进行了运动学、动力学建模与分析;杜中秋等[6]设计了一种可用作快递中转站的智能分拣、投递的具有部分运动解耦性的2T1R并联机构,并进行了刚度与动力学分析。这些机构同时具有符号式位置正解及部分运动解耦性。邹建星等[7]提出了一种新型3自由度2T1R机构,并采用了一种高效的波纹搜索法,求得并联机构工作空间;张彦斌等[8]提出一种新型非对称2T1R空间并联机构,并对其结构进行变形演化,使机构末端执行器的转动能力大幅度提高。这些机构具有符号式位置正解且具有完全运动解耦性。在机构位置求解上[9],大多数学者应用杆副法[10-11]、回路法[12-14]建立机构位置方程,但所含变量数目多、变量之间的耦合性强,其数学消元过程十分复杂。杨廷力[15]提出了机构运动学分析的序单开链法,解决了复杂平面机构位置分析问题;沈惠平[16]提出了并联机构的拓扑特征运动学建模原理和方法,具有求解简便、计算量小等优势。
动力学建模方法主要有:Lagrange法[17]、Newton-Euler法[18]、虚功原理[19]等。徐奕柳等[20]基于Lagrange方程建立了PURU+RR+S球面并联人形机器人踝关节的动力学模型,并对机构运动学及动力学模型进行了验证;翟国栋等[21]基于Newton-Euler法对6自由度并联机构进行动力学前馈控制分析,验证了该方法可有效提高机构运动精度;朱小蓉等[22] 基于Newton-Euler法建立一种3T1R解耦并联机构的动力学模型,并对其动力学性能和惯量耦合强度进行了分析;KALANI 等[23]基于虚功原理提出了一种能缩短计算时间、提高精度的改进型动力学普遍方程,并对 Gough-Stewart 机构进行了正逆动力学分析。
本文根据基于方位特征方程的并联机构设计理论[24],设计由低副组成、设计与制造方便的3自由度2T1R并联机构,并分析机构运动学和动力学性能,该机构耦合度为零、位置正解符号化且部分运动解耦。
1.1.1 串、并联机构拓扑设计基本方程
串联机构末端构件、并联机构动平台POC方程分别为[24]
(1)
(2)
式中 Mbi——第i条支链末端构件POC集
MJk——第k个运动副POC集
MSj——第j个子链POC集
Mpa——机构动平台POC集
1.1.2 支链设计
为设计两平移一转动(2T1R)并联机构,设计一条混合支链Ⅰ、一条约束支链Ⅱ,其末端构件的POC集至少应包含2T1R元素,具体如下:
(1)混合支链Ⅰ设计
首先设计一个具有两个分支链的两平移运动特性的空间子并联机构,如图1a所示,分支链1、2分别为:P1⊥R11‖R12、P2⊥P(4R)。2条分支链分别通过移动副P1、P2布置于同一条导轨上。为便于阐述,在静平台0上建立坐标系OXYZ,X轴向平行于P1轴线方向,Y轴向垂直于P1轴线方向,Z轴向平行于静平台0法线方向。
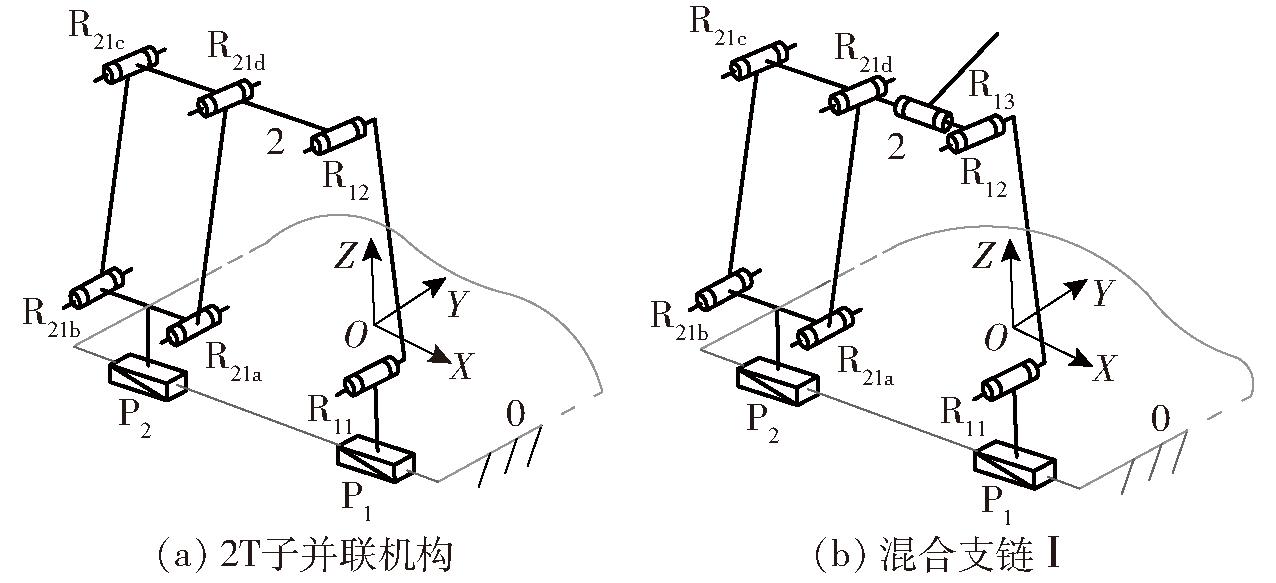
图1 混合支链Ⅰ设计过程
Fig.1 Design of hybrid branching chain Ⅰ
由式(1)得分支链1、2的POC集
由式(2)可得,该子并联机构末端输出杆2的POC集为
Msub=M1∩M2=
因此,图1a所示子并联机构末端构件输出运动为两平移(2T)。
在子并联机构输出杆2上,再串联一个与转动副R12轴线垂直的转动副R13,由此可得到混合支链Ⅰ,即:P1⊥R11‖R12⊥R13⊥P(4R)⊥P2,如图1b所示,并将其与动平台1的一端相连接。取R13为基点O′。
由式(1)知,混合支链Ⅰ末端构件POC集为
表明,混合支链Ⅰ末端构件输出运动为XOZ平面内的二维平移(2T)以及绕R13轴线的一维转动(1R),正是待设计机构动平台1期望的POC。
(2)约束支链Ⅱ设计
约束支链Ⅱ末端构件POC至少为两平移一转动(2T1R),为此,设计1条由1个移动副(P3)和2个平行轴线的转动副组(R31‖R32)、(R33‖R34)串联而成的简单支链,且两个转动副组的轴线相互垂直,其可表示为:P3⊥R31‖R32⊥R33‖R34,如图2所示。
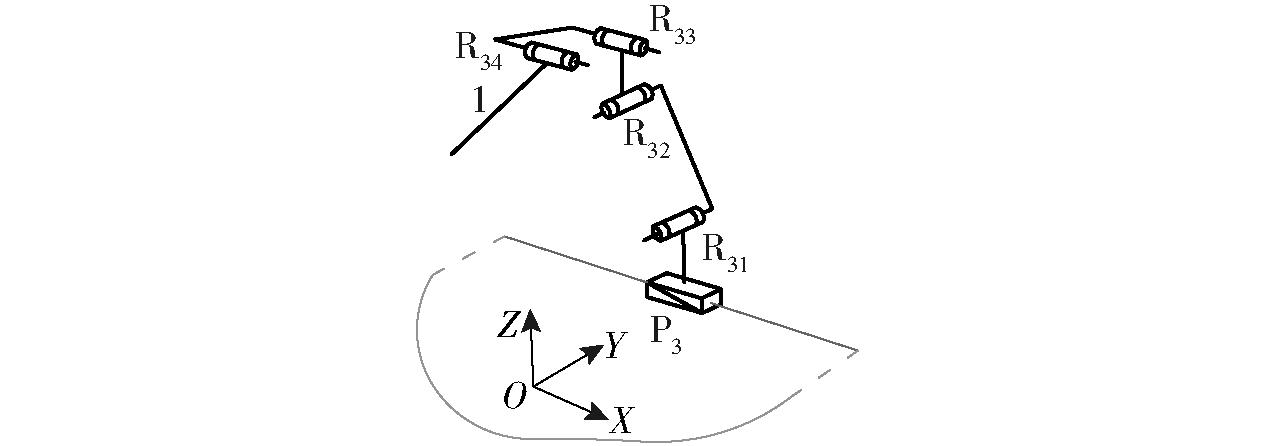
图2 约束支链Ⅱ
Fig.2 Design of constraint branching chain Ⅱ
由式(2)知,约束支链Ⅱ末端构件POC集为
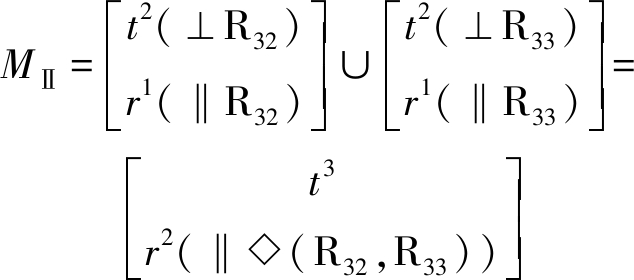
此式表明,约束支链Ⅱ末端构件能产生三平移(3T)及平行于R32、R33轴线组成平面内的二维转动(2R)。
1.1.3 机构设计
将上述混合支链Ⅰ与约束支链Ⅱ并联连接于静平台0、动平台1之间,且在静平台0上,混合支链Ⅰ中的移动副P1、P2与约束支链Ⅱ中的P3平行, 动平台1上的转动副R13、R34轴线相互平行,从而设计出3自由度的2T1R并联机构,如图3所示。
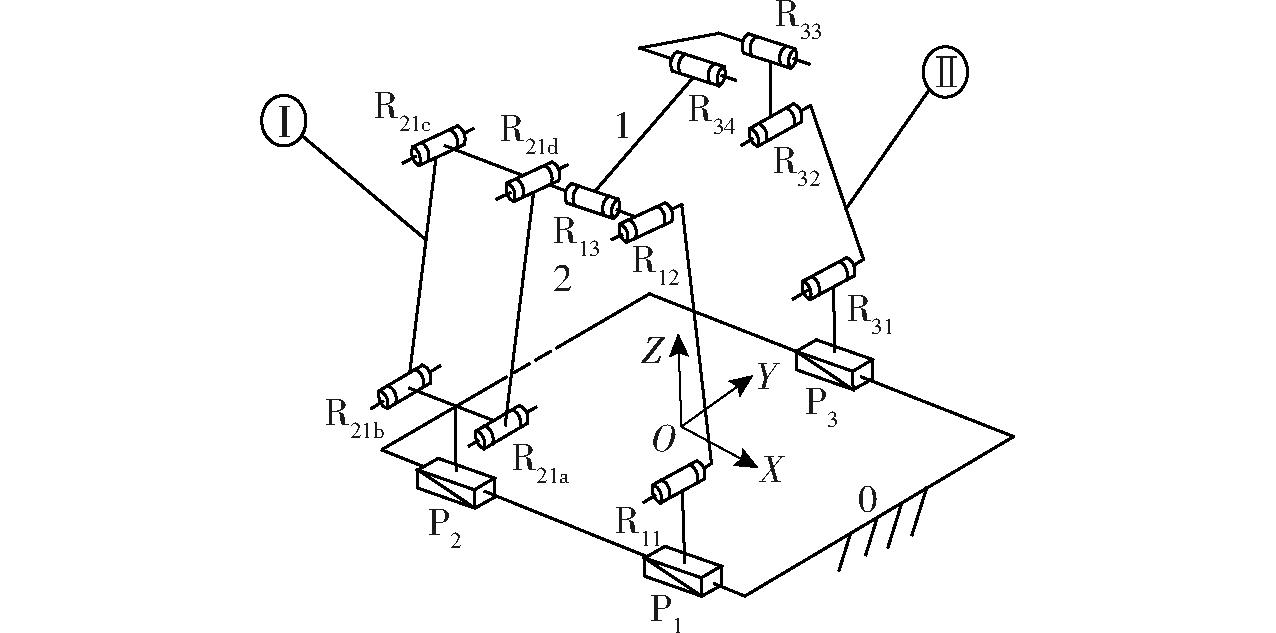
图3 2T1R并联机构简图
Fig.3 Schematic of 2T1R parallel mechanism
由式(2)可确定机构动平台POC集为
Mpa=MⅡ∩MHSOCⅠ=
表明机构动平台1具有两平移一转动的特性。
并联机构非瞬时DOF公式[24]为
(3)
其中
(4)
式中 F——机构自由度
fi——第i个运动副的自由度
v——独立回路数
ξLj——第j个回路的独立位移方程数
前j条支链组成的子并联机构POC集
Mb(j+1) ——第j+1条支链末端POC集
显然,该机构包含两个独立回路,具体为:①第1回路为混合支链Ⅰ中的平面并联机构,即Loop1{-P2‖P(4R)⊥R12‖R11⊥P1-}。其独立位移方程数ξLj=3,输出为两平移。②第2回路由混合支链Ⅰ(子并联机构和串联转动副R13)和约束支链Ⅱ组成,记为Loop2{-P3⊥R31‖R32⊥R33‖R34‖R13-},由式(4)得其独立位移方程数
由式(3)可得机构自由度为
因此,该机构自由度为3。当取静平台0上的移动副P1、P2、P3为驱动副时,动平台1可实现一个沿XOZ平面的两维平移和一个绕X轴的一维转动的运动输出。
由基于单开链(SOC)的机构组成原理知,任一机构可分解为约束度为正、零、负的3种有序单开链(SOC),第j个SOC的约束度定义为[24]
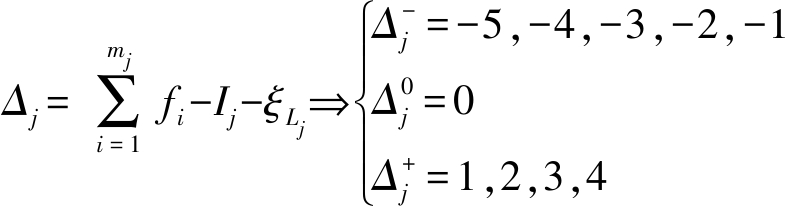
(5)
式中 mj——第j个SOC的运动副数
Ij——第j个SOC的驱动副数
对一个SKC的耦合度为[17]
(6)
其中,
表示将SKC分解为v个
取值为最小者。
κ揭示了机构回路运动变量之间的关联程度;κ越大,机构耦合性越强,运动学、动力学分析复杂度越高。
由式(5)求得第1、2回路的约束度分别为
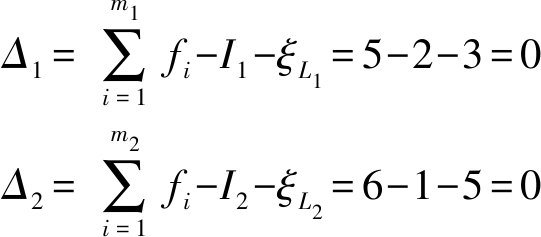
由SKC的判定准则[16]知,上述两个回路单独构成两个子运动链求解,即SKC1、SKC2。其耦合度κ分别由式(6)求得
该机构运动学模型如图4所示,以矩形静平台0的几何中心O为原点,建立笛卡尔静坐标系OXYZ,Y轴平行于D1E3,X轴平行于A1A2,Z轴平行于导轨所在平面的法线方向;动坐标系O′X′Y′Z′原点位于动平台1的R13几何中心,X′轴与D1C1重合,Y′轴垂直于D1C1连线且平行于定平台平面,而Z′轴由右手定则确定。设:lAiBi=l1(i=1,2,3),lB1C1=l2,lB3C3=l3,lC3D3=l4,lD3E3=l5,lE2D2=l6,lB2C2=l7,lD2D1 =lD1C1=l8;静平台上两轨道间距离为2a,动平台上lD1E3=l9。
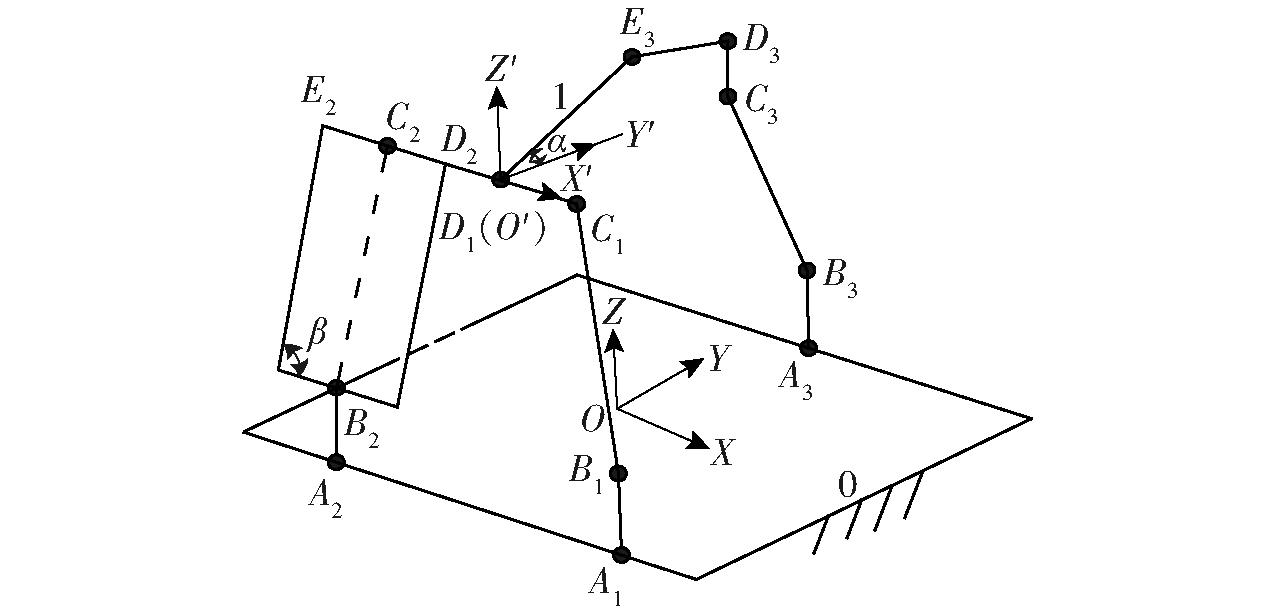
图4 机构运动学模型
Fig.4 Kinematics model of mechanism
设D1E3与Y′轴正向夹角为动平台1输出姿态角α,平行四边形短杆与长杆的夹角为β。
位置正解问题为:已知静平台上3个点Ai(i=1,2,3)的移动量为x1、x2、x3,求动平台1上点O′的位置(x,y,z)以及动平台姿态角α。
(1)SKC1位置求解
在静坐标系OXYZ中,易知各点坐标为
A1=(x1,-a,0) A2=(x2,-a,0) A3=(x3,a,0)B1=(x1,-a,l1) B2=(x2,-a,l1)B3=(x3,a,l1)C2=(x2+l7cosβ,-a,l1+l7sinβ) D2=(x2+l6/2+l7cosβ,-a,l1+l7sinβ)D1=O′=(x2+l6/2+l7cosβ+l8,-a,l1+l7sinβ)C1=(x2+l6/2+l7cosβ+2l8,-a,l1+l7sinβ)
由杆长约束条件lB1C1=l2建立的位置方程解得
其中
将β代入点O′可得
(7)
(2)SKC2位置求解
易有A3=(x3,a,0),B3=(x3,a,l1)。
由D1-E3-D3组成回路在YOZ平面上的投影,有
E3=(x,-a+l9cosα,z+l9sinα)D3=(x,a,ZD3)C3=(x,a,ZD3-l4)
其中
由杆长约束条件lB3C3=l3建立位置方程,解得
(8)
其中
K=-l4+l7sinβ
至此,动平台1的位置O′(x,y,z)及姿态角α已全部求得,即
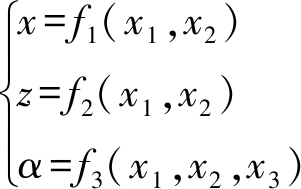
表明:该机构不仅有符号式位置正解,而且具有I-O部分运动解耦性,即点O′的x、z由输入量x1、x2决定,α由x1、x2、x3共同确定。该机构位置正解个数为8。
位置逆解问题为:已知动平台1位置O′(x,y,z)及姿态角α,求3个移动驱动副的输入x1、x2、x3。
由式(7)解得
(9)
将式(9)代入式(7)可解得
(10)
由杆长约束条件lB3C3=l3、lB1C1=l2可解得
(11)
(12)
其中
综上,当动平台1上点O′的坐标(x,y,z)和姿态角α已知时,x1具有2组解,x3具有4组解,因此,该机构具有8组逆解。
设该机构结构参数为:a=100 mm,l1=40 mm,l2=95 mm,l3=60 mm,l4=40 mm,l5=76 mm,l6=36 mm,l7=95 mm,l8=25 mm,l9=125 mm。
设3个移动输入量x1、x2、x3分别为:61.783 3、-62.400 8、56.223 0 mm。
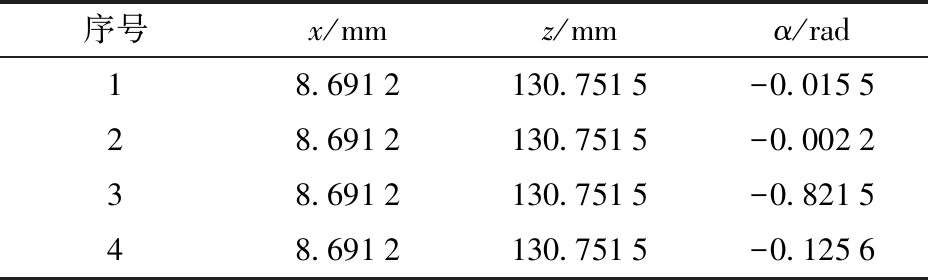
利用Matlab编程,可得8组正解,其中,4组实数解如表1所示。
表1 机构位置正解值
Tab.1 Positive value of position of mechanism
序号x/mmz/mmα/rad18.6912130.7515-0.015528.6912130.7515-0.002238.6912130.7515-0.821548.6912130.7515-0.1256
将表1中第1组数据代入式(10)～(12),得到8组逆解,其中4组实数逆解值如表2所示。
表2 机构位置逆解值
Tab.2 Inverse solution of position of mechanism mm
序号x1x2x3161.7833-62.400856.223023461.78335.59915.5991-62.4008-62.4008-62.4008-38.839156.2230-38.8391
可见,表2中第1组逆解,与正解求解时给定的3个输入量一致。
利用Solidworks软件得到的动平台位姿仿真曲线也与理论曲线一致,从而验证了位置正逆解的正确性。
当机构处于非奇异位形时,雅可比矩阵Jp存在逆矩阵。因此,可推导出速度公式为
(13)
其中
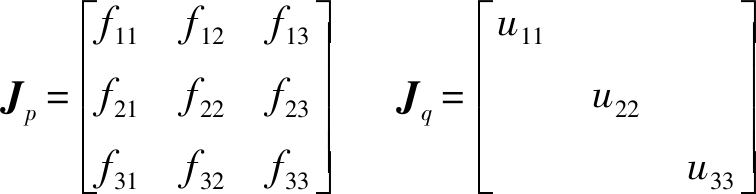f11=2(x-x1)+50 f12=2z-80 f13=0f21=2(x-x2)-86 f22=2z-80 f23=0f31=2(x-x3)
u11=2(x-x1)+50 u22=2(x-x2)-86
u33=2(x-x3)
式(13)即为动平台基点的速度输出公式,对式(13)继续求导,可得
(14)
其中
K=[K1 K2 K3]T
设3个驱动副输入速度均为
则其驱动副的输入加速度均为
用Matlab编程得到动平台基点速度与加速度理论曲线;与通过Solidworks仿真得到动平台速度与加速度仿真曲线完全一致,如图5、6所示。
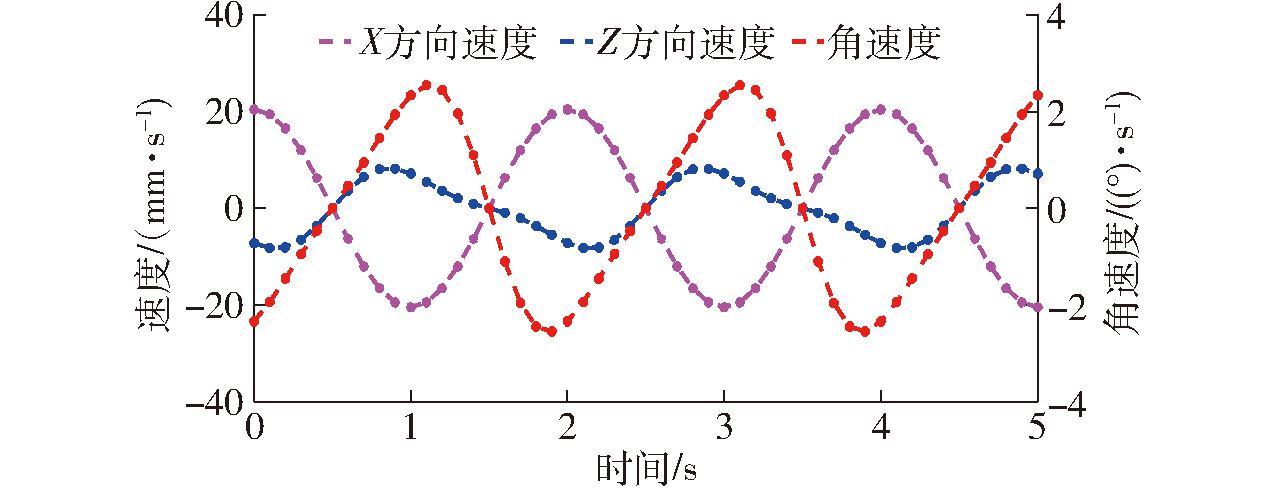
图5 动平台基点速度理论计算曲线
Fig.5 Theoretical calculation curves of base point velocity of moving platform
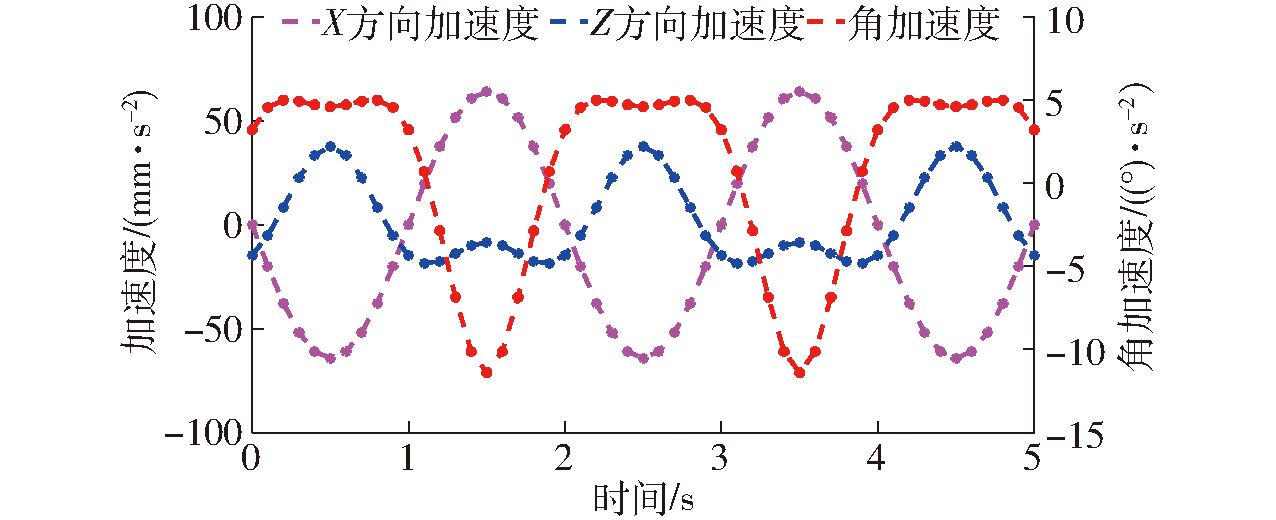
图6 动平台基点加速度理论计算曲线
Fig.6 Theoretical calculation curves of base point acceleration of moving platform
由图5、6可知,机构速度、加速度理论值与用Solidworks得到的仿真曲线一致,验证了运动学模型的正确性。
其余杆件速度、加速度可由理论力学的运动合成定理分别求得。限于篇幅,此处不再列出。
根据矩阵Jp、Jq是否奇异,将机构奇异位形分为
(1)当det(Jq)=0时,机构发生输入奇异。
(2)当det(Jp)=0时,机构发生输出奇异。
(3)当det(Jp)=det(Jq)=0时,机构发生综合奇异。
由式(13)得,输出速度V和驱动输入ρ的关系为
JpV=Jqρ
3.2.1 输入奇异
当det(Jq)=0时,机构发生输入奇异,有3种情况(注:绿色表示静平台,蓝色表示动平台,红色表示输入驱动)。
(1) u11=2(x-x1)+50=0,即点A1与C1的X轴的坐标相等,如图7a所示。
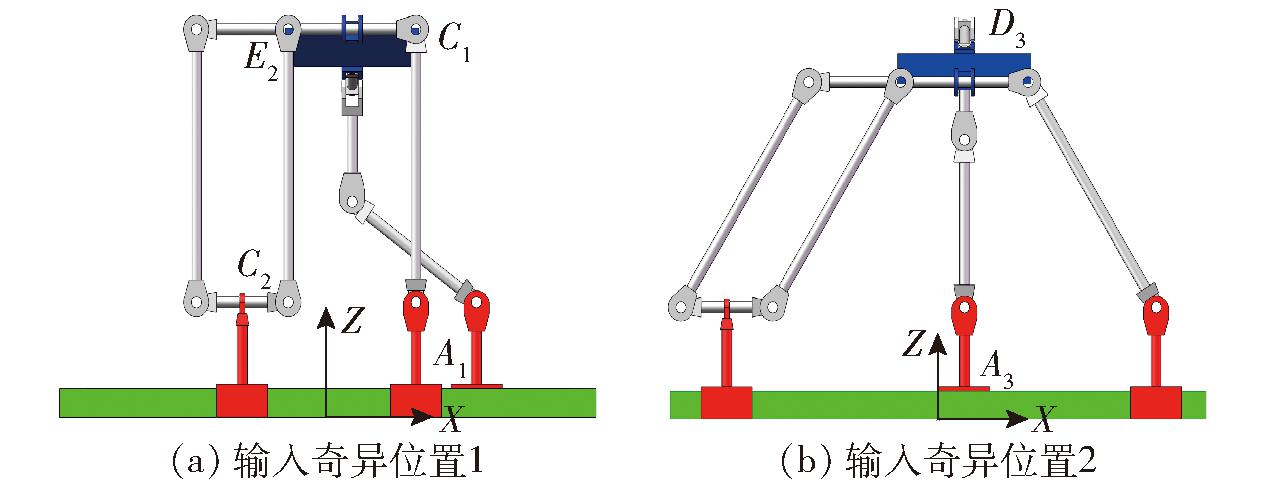
图7 机构输入奇异位置
Fig.7 Mechanism input singular position
(2)u22=2(x-x2)-86=0,即点C2与E2的X轴的坐标相等,如图7a所示。
(3)u33=2(x-x3)=0,即点A3与D3的X轴坐标相等,如图7b所示 。
3.2.2 输出奇异
当det(Jp)=0时,现将矩阵转换为三角矩阵,故机构发生输出奇异有3种位形。
(1)f11=2(x1-x2)+50=0,即杆C2E2竖直且杆C2E2与杆B1C1在XOZ平面内的投影平行时,机构将发生输出奇异。
(2)f22=2z-80=0,即点C2与E2的Z轴坐标相等;由于杆件干涉达不到该位置,因此,该奇异位置不存在。
(3)f33=0,即当动平台的姿态角满足α=0°时,机构发生输出奇异。
3.2.3 综合奇异
当det(Jp)=det(Jq)=0时,机构发生综合奇异。经分析该机构无综合奇异位形。
在考虑机构杆件干涉、运动副转角约束的前提下,采用位置正解计算工作空间。初步设定3个移动驱动副的工作范围:-100 mm≤x1≤100 mm,-100 mm≤x2≤100 mm,-100 mm≤x3≤100 mm, 用Matlab编程求得动平台上基点O′的工作空间,如图8所示。
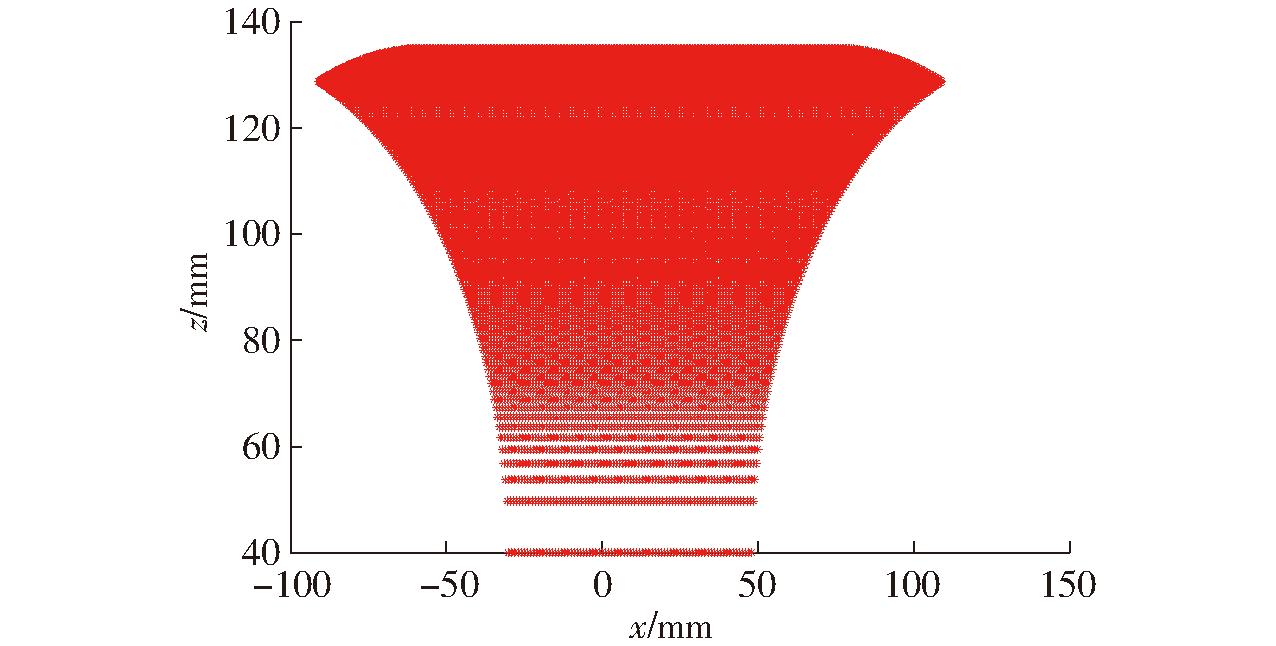
图8 2T1R机构工作空间
Fig.8 2T1R mechanism workspace
5.1.1 基于虚功原理的序单开链法基本原理
对自由度为f、广义速度为
的机械系统,基于单开链(SOC)的机构组成原理,将其分成若干个子运动链(SKC),而每一个子运动链又可拓扑分解为若干个单开链
假定解除原系统若干个运动副的k 个约束后,解除的运动副支反力将转换为作用在新系统构件上的未知外力。相应新系统增加的广义速度记作
按照上述拓扑结构分解的逆序,对各单开链进行动力学分析,由单开链之间的约束关系和虚功原理可知:在理想约束下,外力(矩)和惯性力(矩)在机械系统的任何虚位移上的元功之和等于零,即可建立各SKC的动力学分析方程。
5.1.2 受力分析
因该并联机构由2个零耦合度的SKC组成,故可分别在SKC1、SKC2内对各杆件进行受力分析。
(1)SKC2内各杆件受力分析
取动平台质心为点p,则有
(15)
式中 fp——动平台所受外力
τp ——动平台所受外力矩
a1——动平台加速度
mp——动平台质量
g——重力加速度
ω1 ——动平台角速度
ε1——动平台角加速度
Ip ——动平台相对于坐标系OXYZ 的惯量矩阵
移动滑块A3B3受力,即
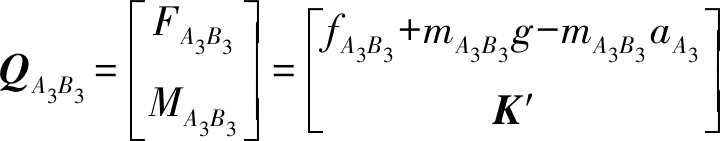
(16)
其中
式中 mA3B3——滑块 A3B3质量
fA3B3——滑块 A3B3上的驱动力
杆件 B3C3受力,即
(17)
式中 mB3C3——杆B3C3质量
IB3C3——杆B3C3相对于坐标系OXYZ惯量矩阵
杆件C3D3受力,即
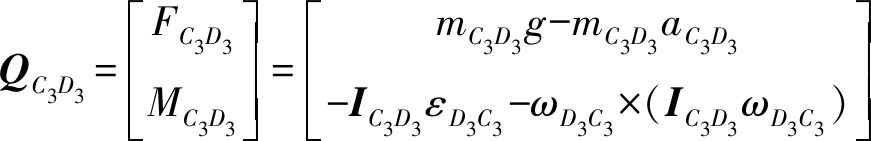
(18)
式中 mC3D3——杆 C3D3质量
IC3D3——杆C3D3相对于坐标系 OXYZ惯量矩阵
杆件D3E3受力,即
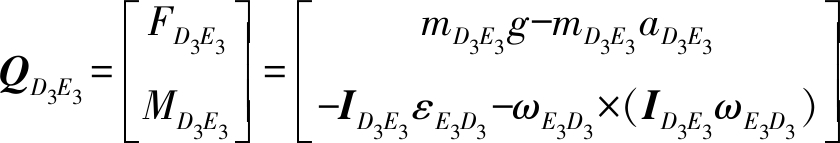
(19)
式中 mD3E3——杆D3E3质量
ID3E3——杆D3E3相对于坐标系OXYZ惯量矩阵
(2)SKC1内各杆件受力分析
驱动滑块AiBi(i=1,2)受力,即
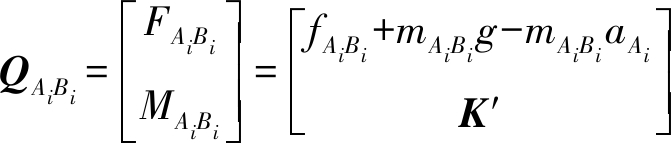
(20)
式中 mAiBi——滑块AiBi质量
fAiBi——滑块AiBi上的驱动力
杆件B1C1受力,即
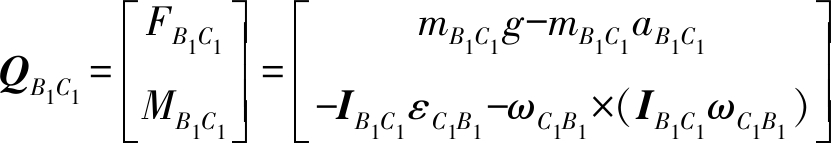
(21)
式中 mB1C1——杆B1C1质量
IB1C1——杆B1C1相对于坐标系OXYZ惯量矩阵
由于平行四边形的短杆只产生平行移动,故其受力为
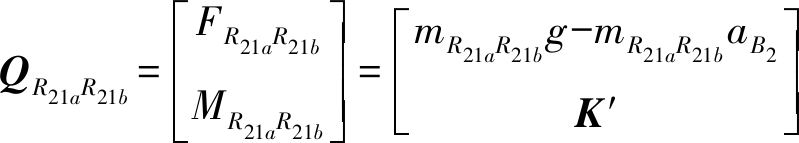
(22)
式中 mR21aR21b——平行四边形短杆R21aR21b总质量
在平行四边形结构中,因为平行四边形两长杆具有相同的速度和加速度,故可等效为一个转动杆B2C2,则有
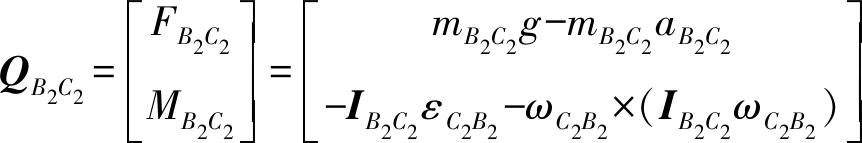
(23)
由于杆件E2D2、D2C1均在XOZ面运动,且两杆同轴线,不发生相对转动,故这里将杆件E2D2 和杆件D2C1视为同一杆件E2C1,则有
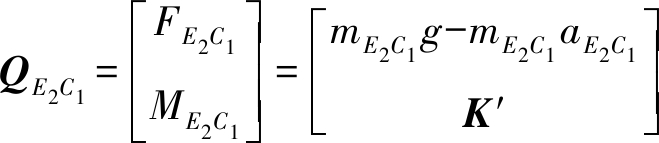
(24)
式中 mE2C1——杆件E2D2和杆件D2C1总质量
5.1.3 动力学方程建立
解除运动副R13的约束,即D1处的约束,得到SKC1、SKC2两个子系统,于是,支反力FD1转换为作用在该两个子系统构件上的未知外力。根据基于虚功原理的序单开链法,可得SKC2动力学方程为
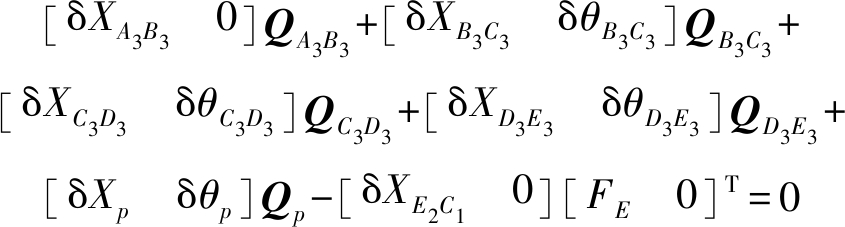
(25)
SKC1动力学方程为
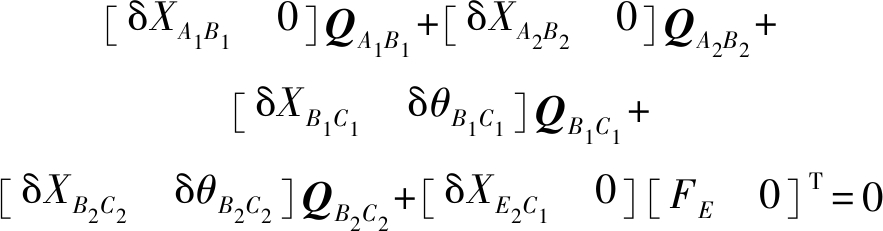
(26)
其中
δXAiBi=JvAiBiδq (i=1,2,3)δXBiCi=JvBiCiδq (i=1,2,3)δXC3D3=JvC3D3δq δXD3E3=JvD3E3δqδXp=Jvpδq δXE2C1=JxδqδθBiCi=Jwδq (i=1,2,3)δθC3D3=Jwδq δθD3E3=Jwδq δθp=Jwδq
5.2.1 杆件参数
设机构中各杆件质量分别为: mAiBi=3.681 5 kg(i=1,3),mA2B2=3.219 1 kg,mB1C1=3.311 7 kg,mB3C3=2.305 8 kg,mC3D3=2.494 0 kg,mD3E3=2.455 9 kg,mE3D1=13.842 2 kg,mB2C2=3.764 8 kg,mR21aR21b=1.306 3 kg,杆件转动惯量见表3。
表3 各杆件的转动惯量参数
Tab.3 Moment of inertia parameters of each member
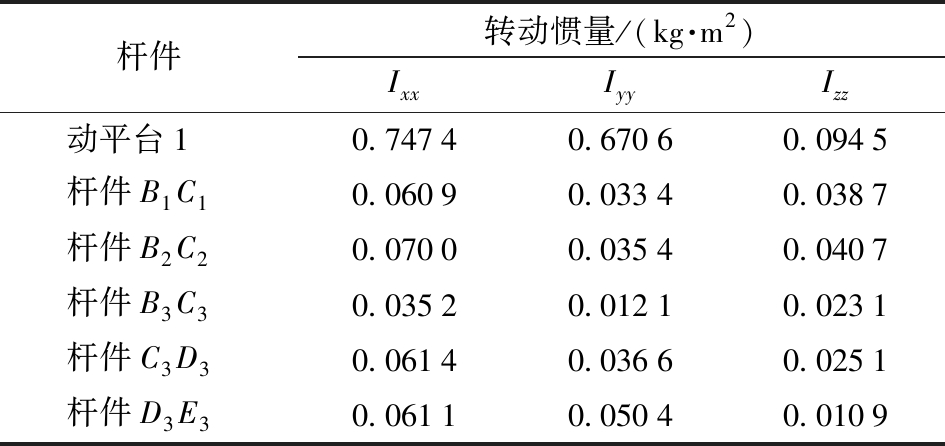
杆件转动惯量/(kg·m2)IxxIyyIzz动平台1 0.74740.67060.0945杆件B1C10.06090.03340.0387杆件B2C20.07000.03540.0407杆件B3C30.03520.01210.0231杆件C3D30.06140.03660.0251杆件D3E30.06110.05040.0109
5.2.2 驱动力及支反力求解
将上述参数代入式(15)～(26),将2.4节的输入函数作为驱动副的输入,用 Matlab计算(忽略摩擦时)该机构在负载20 kg状态下的驱动力,如图9所示;同时,将虚拟样机导入ADAMS中,选取运动仿真时间为8 s,进行仿真,得到一致的驱动力仿真曲线。
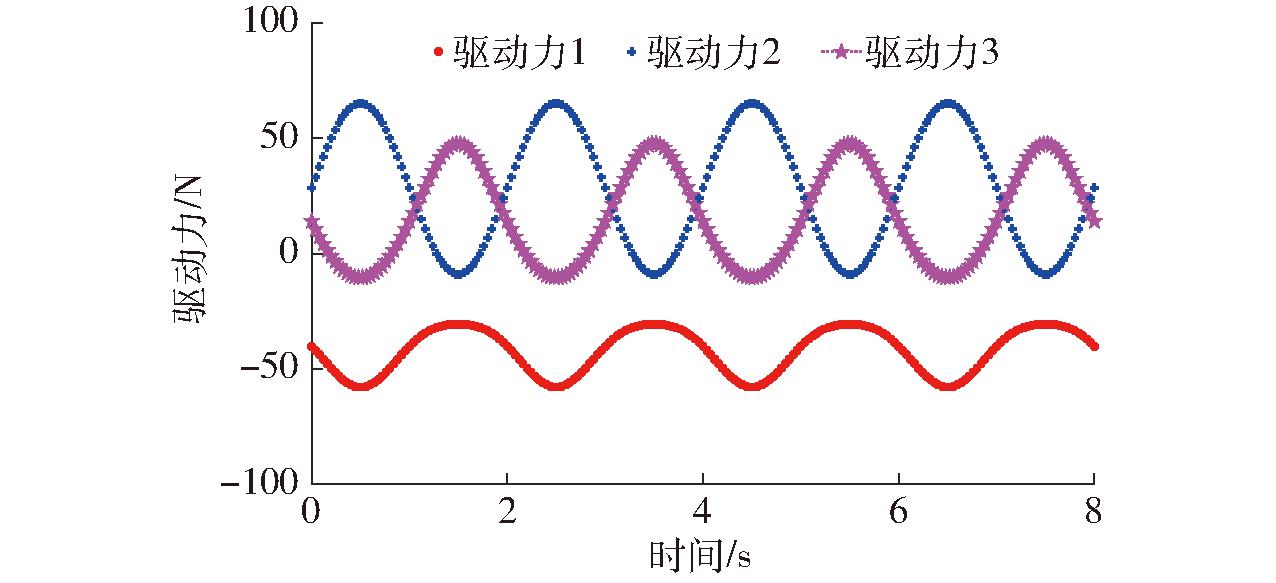
图9 驱动力曲线
Fig.9 Driving force curves
由式(25)可得R13处的支反力的理论计算曲线,如图10所示。同样,通过ADAMS仿真,得到一致的R13处支反力的仿真曲线,从而验证了机构动力学模型正确性。
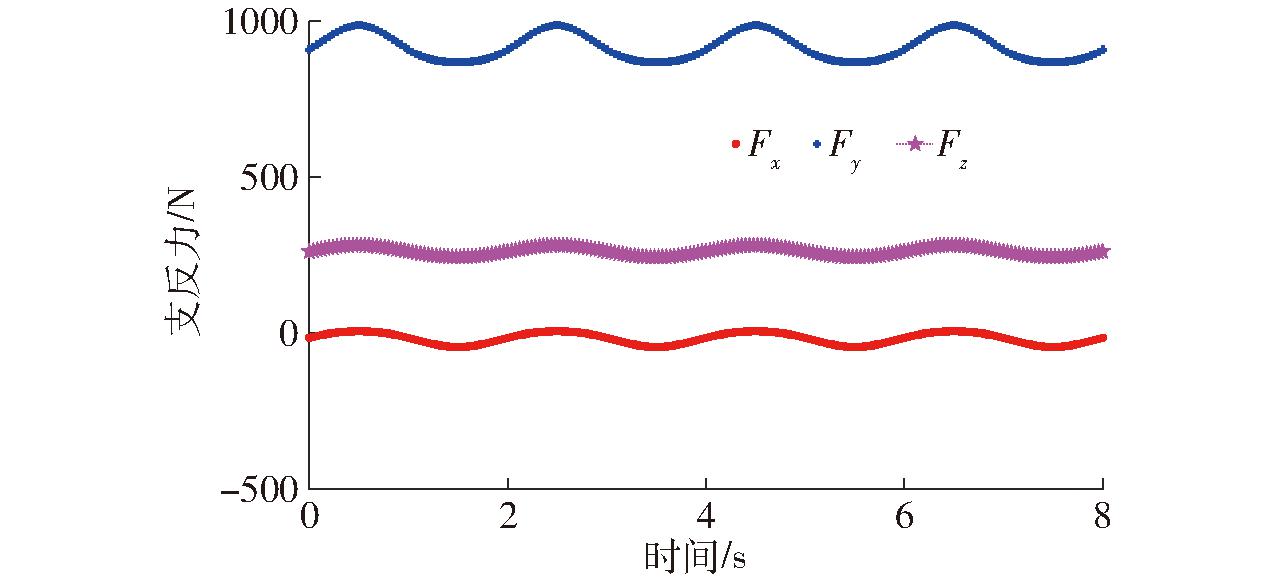
图10 R13处支反力曲线
Fig.10 Support reaction curves at R13
由图9可知,3个滑块所需的最大驱动力分别为:-58.52、47.28、64.10 N,这为驱动电机选择奠定了技术基础。
目前,大多数无人机自适应降落(主动式、被动式)和空中作业(串联、并联机械臂)两种功能分开;同时具备自适应降落和现空中作业的无人机研究较少[25]。
作为应用场景之一,该机构可用于无人机末端执行器及安全着陆装置,如图11所示,它具有3个优点:①同时具备自适应降落及空中作业的能力,避免了双模式(降落、操作)切换下出现奇异位型[25]。②具有部分运动解耦性,运动控制方便,且运动平缓、动力学性能良好。③自适应降落时,以机构动平台与地面接触,受到地面的冲击力较小。
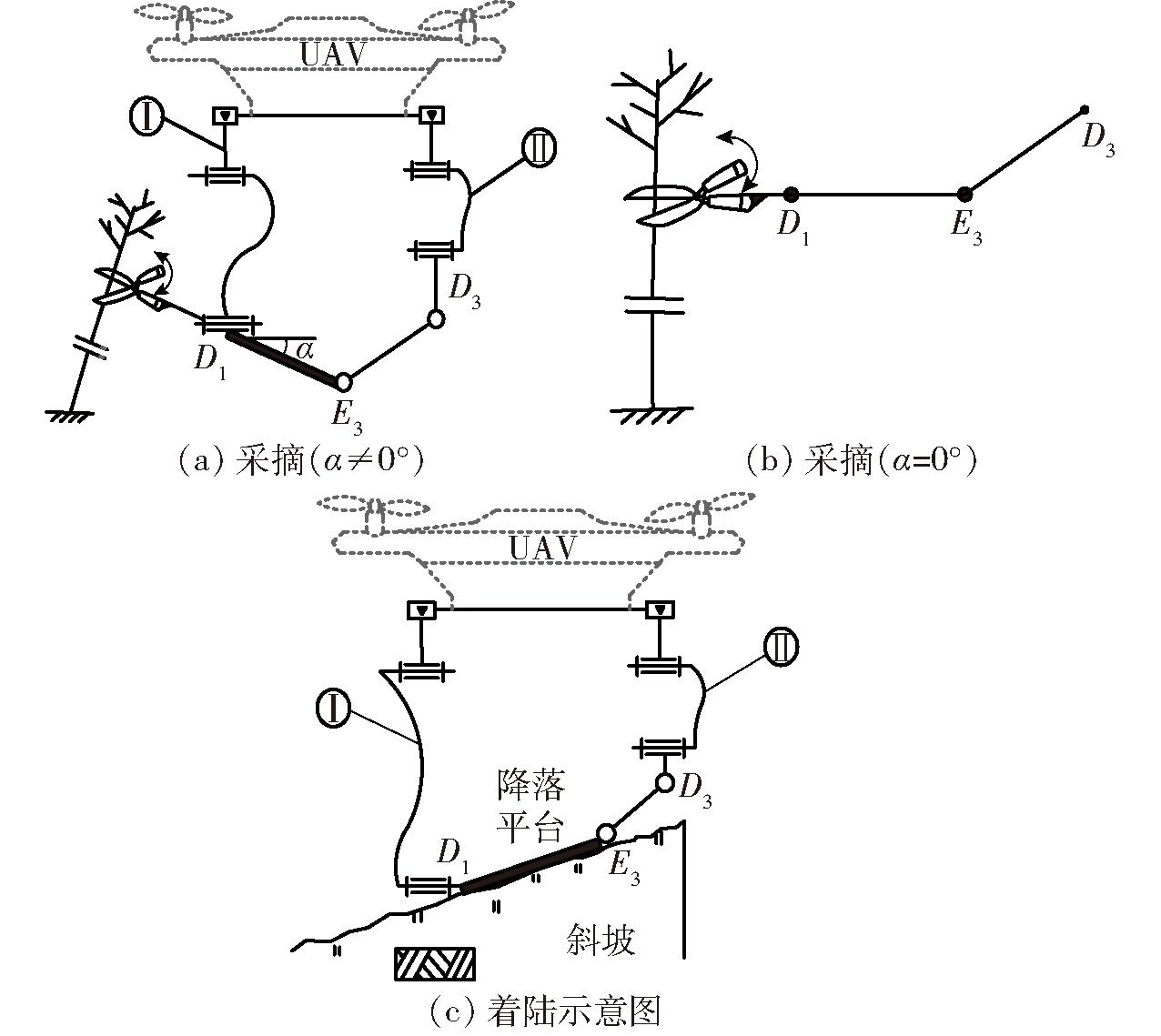
图11 应用场景原理图
Fig.11 Schematics of application scenarios
将该机构静平台固定在无人机下方的底座上,可用于无人机的末端执行器进行空中的两平移一转动操作,例,空中变姿态的喷撒(农药、种子等)、采摘(茶叶、水果等)和搬运等;可使无人机自适应地降落在倾斜的陆地上,防止其倾覆以安全着陆。其工作原理是:①用作无人机执行器。如图11a、11b所示,机构动平台用作末端执行器,例,在末端执行器上安装一把采摘剪刀,可完成水果采摘任务(剪刀开合动作可采用电磁铁驱动),其两维移动可以调节采摘剪刀距离采摘目标(茶叶、水果等)的高度和远近距离,一维转动可以调节剪刀与待采摘目标物姿态角α,以便剪刀能精细化地完成采摘任务。②用作无人机安全着陆器。如图11c所示,机构动平台用作着陆端,当无人机准备着陆时,安装于无人机底部机器视觉完成对着陆地形的识别,后控制器自动使3个移动驱动副作差速运动,此时,动平台可实现两维移动和一维转动,其中,两维移动可以调节2条支链距离着陆地的高度及位置,一维转动可以调节动平台转角,以便无人机能平稳降落在倾斜的陆地上。
(1)设计了一种由低副组成的2T1R并联机构,该机构结构简单、制造/装配容易;同时,具有部分输入-输出解耦性,对机构的轨迹规划和运动控制十分有利。
(2)基于拓扑特征运动学原理,求解了机构运动学符号式正反解;分析了该机构的奇异位置;基于符号式位置正解的工作空间分析表明:该机构具有较大的工作空间。
(3)根据基于虚功原理的序单开链法,建立了该机构动力学模型,求得了机构驱动力,表明该机构运动平缓、动力学性能良好。
(4)该机构可集成无人机末端执行器与安全着陆两种功能,一方面,用于无人机的末端执行器进行空中的两平移一转动(2T1R)操作,另一方面,可使无人机自适应地降落在倾斜的陆地上,防止其倾覆以安全着陆。
[1] 柳纪琛,吴孟丽,王明曦,等.一种2T1R并联机构的运动分析及尺度优化[J].机械设计,2020,37(12):71-81.LIU Jichen,WU Mengli, WANG Mingxi, et al. Kinematics analysis and scale optimization of a 2T1R parallel mechanism[J]. Journal of Machine Design, 2019,37(12):71-81.(in Chinese)
[2] LI Y,ZHANG Y,ZHANG L. A new method for type synthesis of 2R1T and 2T1R 3-DOF redundant actuated parallel mechanisms with closed loop units[J].Chinese Journal of Mechanical Engineering,2020,33(6):144-167.
[3] 张彦斌,刘宏昭,吴鑫,等.2T1R弱耦合并联机构的运动学和奇异性分析[J].农业机械学报,2008,39(4):132-136.ZHANG Yanbin, LIU Hongzhao, WU Xin, et al. Kinematics and singularity analysis of 2T1R weakly coupled parallel mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery,2008,39(4):132-136.(in Chinese)
[4] LI J, HE H, WU G, et al. Three 2-DOF 1T1R and one 3-DOF 2T1R full-hinged novel parallel mechanisms with zero coupling degree and motion decoupling: design and analysis[J]. ASME. J. Mechanisms Robotics March, 2024, 16(3): 031003.
[5] 沈惠平,朱晨阳,李菊,等.零耦合度部分运动解耦 2T1R并联机构拓扑与性能研究[J].农业机械学报,2023,54(2):419-429,440.SHEN Huiping, ZHU Chenyang, LI Ju, et al. Topology and performance of zero-coupling partially kinematic decoupled 2T1R parallel mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery,2023,54(2):419-429,440.(in Chinese)
[6] 杜中秋,沈惠平,李菊,等.一种位置正解符号化且运动部分解耦的新型2T1R并联机构动力学分析[J].机电工程,2023,40(8):1231-1239.DU Zhongqiu, SHEN Huiping, LI Ju, et al. Dynamic analysis of a novel 2T1R parallel mechanism symbolized by position-solution and decoupling of moving parts[J]. Mechanical and electrical Engineering, 2023,40(8):1231-1239.(in Chinese)
[7] 邹建星,罗玉峰,石志新,等.一种新型2T1R并联机构的位置与工作能力分析[J].机械设计与研究,2020,36(3):19-22,29.ZOU Jianxing, LUO Yufeng, SHI Zhixin, et al. Analysis of position and working capability of a new 2T1R parallel mechanism[J]. Machine Design and Research, 2019,36(3):19-22,29.(in Chinese)
[8] 张彦斌,张树乾,吴鑫.空间2T1R型并联机器人机构的设计与运动学分析[J].机械科学与技术,2014,33(4):484-489.ZHANG Yanbin, ZHANG Shuqian, WU Xin. Design and kinematics analysis of space 2T1R parallel robot mechanism[J]. Mechanical Science and Technology for Aerospace Engineering,2014,33(4):484-489.(in Chinese)
[9] MICHEAL MCCARTHY J.21st century kinematics[M].London:Springer,2012.
[10] ROONEY G T. Constraint approach to displacement analysis of planer linkages[J].Mechanism,1972(9):60-63.
[11] JAL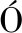
N J G D, SERNA M A, AVIL
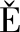S R, et al. Computer method for kinematic analysis of lower-pair mechanisms[J]. Mechanism &Machine Theory, 1981, 16(5): 543-566.
[12] KINZEL G L,CHANG C. The analysis of planar linkage using a modular approach[J]. Mechanism and Machine Theory,1984,19(1):165-172.
[13] PENNOCK G R, HASAN A. A polynomial equation for a coupler curve of the double butterfly linkage[J]. Journal of Mechanical Design, 2002, 124(1): 39-46.
[14] KONG X, GOSSELIN C M. Generation and forward displacement analysis of RPR-PR-RPR analytic planar parallel manipulators[J].Journal of Mechanical Design,2001, 8(18): 294-300.
[15] 杨廷力. 机械系统基本理论:结构学、运动学、动力学[M].北京:机械工业出版社,1996.
[16] 沈惠平.机器人机构拓扑特征运动学[M]. 北京:高等教育出版社,2021.
[17] RAT N, NEAGOE M, GOGU G. Theoretical and experimental research on the dynamics of a 4-DOF Isoglide T3R1 parallel robot[C]∥The 11th IFToMM International Symposium on Science of Mechanisms and Machines,2010．
[18] 冯志友, 张燕, 杨廷力, 等. 基于牛顿欧拉法的2UPS-2RPS并联机构逆动力学分析[J]. 农业机械学报, 2009, 40(4): 193-197．FENG Zhiyou, ZHANG Yan, YANG Tingli, et al. Dynamics of a 2UPS-2RPS parallel mechanism by Newton-Euler formulation[J]. Transactions of the Chinese Society for Agricultural Machinery,2009,40(4): 193-197.(in Chinese)
[19] 贾凯凯, 梅江平, 刘松涛, 等. 4自由度并联机构刚体动力学模型[J]. 机械工程学报,2016, 52(13): 10-16．JIA Kaikai, MEI Jiangping, LIU Songtao, et al. Rigid-body dynamic model of a four-DOF parallel mechanism[J]. Journal of Mechanical Engineering,2016, 52(13): 10-16.(in Chinese)
[20] 徐奕柳,杨龙,杨中原,等.新型PURU+RR+S球面并联人形机器人踝关节机构动力学性能分析[J].中国机械工程,2017,28(16):1971-1976.XU Yiliu, YANG Long, YANG Zhongyuan, et al. Dynamic performance analysis of ankle joint mechanism of a new PURU+RR+S spherical parallel humanoid robot[J]. China Mechanical Engineering,2017,28(16):1971-1976.(in Chinese)
[21] 翟国栋,刘龙宇,蔡晨光,等.直线电机驱动六自由度并联机构动力学特性研究[J].农业机械学报,2022,53(11):450-458.ZHAI Guodong, LIU Longyu, CAI Chenguang, et al. Dynamic characteristics of 6-DOF parallel mechanism driven by linear motor[J]. Transactions of the Chinese Society for Agricultural Machinery,2022,53(11):450-458.(in Chinese)
[22] 朱小蓉,赵磊,沈惠平.3T1R解耦并联机构动力学与惯量耦合特性分析[J].农业机械学报,2023,54(9):448-458.ZHU Xiaorong, ZHAO Lei, SHEN Huiping. Coupling characteristics analysis of dynamics and inertia of 3T1R decouple parallel mechanism[J]. Transactions of the Chinese Society for Agricultural Machinery, 2023,54(9):448-458.(in Chinese)
[23] KALANI H, REZAEI A, AKBARZADEH A.Improved general solution for the dynamic modeling of Gough-Stewart platform based on principle of virtual work[J].Nonlinear Dynamics,2016, 83(4):2393-2418．
[24] 杨廷力, 刘安心, 罗玉峰, 等. 机器人机构拓扑结构设计[M]. 北京:科学出版社, 2012:32-140.
[25] 刘建.双模式空中变结构机器人设计与自适应缓冲降落策略研究[D].上海:复旦大学,2023:8-32.LIU Jian. Research on design and adaptive buffered landing strategy of dual-mode aerial variable structure robot[D]. Shanghai: Fudan University,2023:8-32.(in Chinese)