三自由度三平移(3T)并联机器人结构简单、分析方便、控制容易,在现代制造业中有着广泛的应用前景。CLAVEL[1]提出的经典 Delta 3T并联机构,已在工业上得到很好的应用;在此基础上,一些学者提出了相应的类Delta[2-3]机构,TSAI等[4]提出了移动副驱动的三平移并联机构;BOURI等[5]研究了由Delta机构衍生的三平移并联机构。但这些机构不(部分)具备运动解耦特性,运动控制困难。刘延斌等[6]利用螺旋理论设计了全对称、可规避奇异位置的3-RRRU并联机构,并求得其运动学反解;LI等[7]利用螺旋理论分析了三平移并联机构的可动性;WANG等[8]提出了基于瞬时运动学的三平移并联机构;DI GREGORIO等[9-10]设计了3-UPU、3-URC等并联机构;郭宗和等[11]设计了全转动副的非对称三平移并联机构,该机构x、y方向完全解耦,运动控制方便;李丽红等[12]根据基于方位特征方程的并联机构拓扑设计方法,提出并分析了一种弱耦合的2-CPR/UPU三平移并联机构;李菊等[13-14]设计了三平移的并联机构,并采用基于虚功原理的序单开链法,对该机构进行了动力学建模;曾达幸等[15]以螺旋理论为基础,提出移动解耦并联机构分支输入副的选择准则,并设计了新型三平移解耦并联机构;马履中等[16]研究了三平移弱耦合并联机器人;谢俊等[17]提出一种三自由度弱耦合的2T1R并联机构,对其进行位置分析,最后分析了动平台的运动规律;沈惠平等[18-19]提出了两种零耦合度且运动解耦的三平移并联机构,该机构具有较大的工作空间;赵一楠等[20]提出一种可用于抓取的3T并联机构,并以SKC为单元对其进行了运动学、奇异性、工作空间分析;梁栋等[21]提出了一种结构简洁且高效的三平动并联机器人,用以满足高性能3D打印需求;李丽红等[22]针对实时控制的问题,提出一种零耦合度的三平移并联机构,并对其进行了尺寸参数优化;彭红梅等[23]设计一种运动解耦、结构对称、运动副简单、工作空间大的三平移并联机器人机构,并对工作空间的体积进行了优化,工作空间体积较优化前增加12%。这些机构中已有部分运动解耦或符号式位置正解。
本文首先提出一个运动解耦性优异的单回路三平移并联机构,对其进行分析;在此基础上,据此设计一类4种三平移(3T)并联机构。以其中一个机构为例,揭示该机构拓扑学、运动学与动力学性能。
串联、并联机构POC方程分别为[24-25]
(1)
(2)
式中 MJi——第i个运动副的POC集
m——运动副数量
Mbi——第i条支链末端的POC集
n——支链条数
Mpa——机构动平台的POC集
并联机构非瞬时DOF计算式为
(3)
其中![]()
(4)
v=m-n+1
式中 F——机构自由度
fi——第i个运动副自由度
v——独立回路数
ξLj——第j个独立回路的独立位移方程数
![]() 前j条支链组成的子并联机构POC集
前j条支链组成的子并联机构POC集
Mb(j+1)——第j+1条支链末端构件POC集
根据基于单开链(SOC)的机构组成原理可知[14],任一机构可分解为约束度为正、零、负的3种有序单开链(SOC),第j个SOC的约束度计算式为
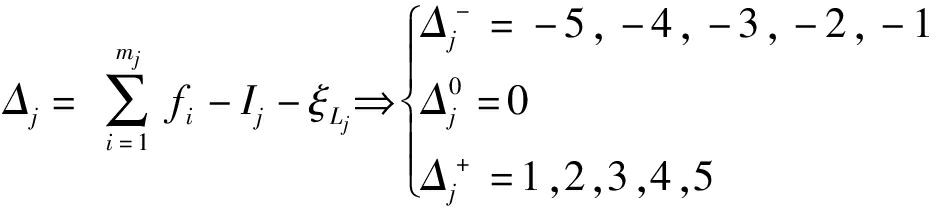
(5)
式中 mj——第j个SOC的运动副数
Ij——第j个SOC的驱动副数
由一组SOC组成的最小子运动链(SKC)耦合度计算式为
(6)
κ表示回路位置变量之间的关联程度,一般地,κ越大,耦合性越强,运动学/动力学分析越复杂。
1.2.1 拓扑设计
提出了一个运动解耦性优异的单回路三平移并联机构,如图1所示,它由动平台1、静平台0及2条相同支链Ⅰ、Ⅱ组成,每条支链都由1个移动副与3个平行轴线转动副(Ri2‖Ri3‖Ri4)(i=1,2)串联连接而成,位于静平台上的两个P副(P11、P21)轴线相互垂直,支链拓扑结构可表示为SOC{-Pi1‖Ri2‖Ri3‖Ri4-}(i=1,2)。
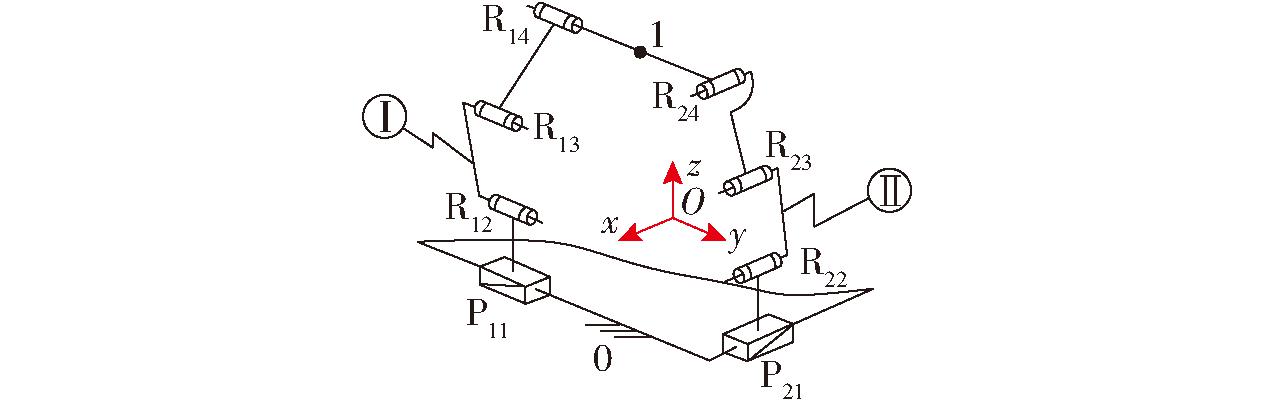
图1 单回路三平移并联机构简图
Fig.1 Schematic of a single-loop three-translation PM
取动平台1上中点O′为一基点,2条支链的POC为

动平台POC集为
由这2条支链构成的回路独立位移方程数ξL1为
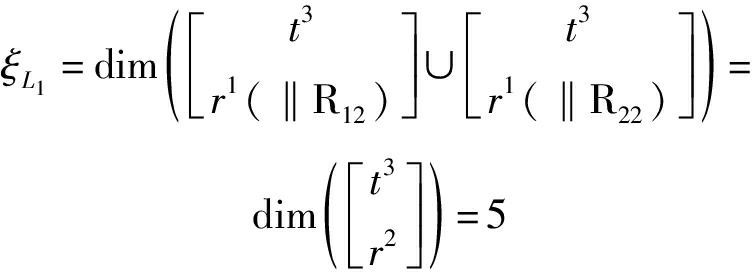
机构自由度F为
因此,机构自由度为3,当取2个滑块(P11、P21)、以及任意1条支链上的1个转动(R12)为驱动副,其动平台1可实现三平移运动输出。
该单回路机构的约束度为
因此,机构的耦合度为零。
1.2.2 位置分析
该并联机构运动学模型如图2所示,以矩形静平台0的几何中心O为原点,建立笛卡尔坐标系Oxyz,y轴平行于A1所在导轨,x轴垂直于y轴,z轴由右手定则确定。点O与A1所在导轨的距离为a,点O与A2所在导轨的距离为b,设lAiBi=l1(i=1,2),lCiBi=l2(i=1,2),lDiCi=l3(i=1,2),lD1O′=lD2O′=d。
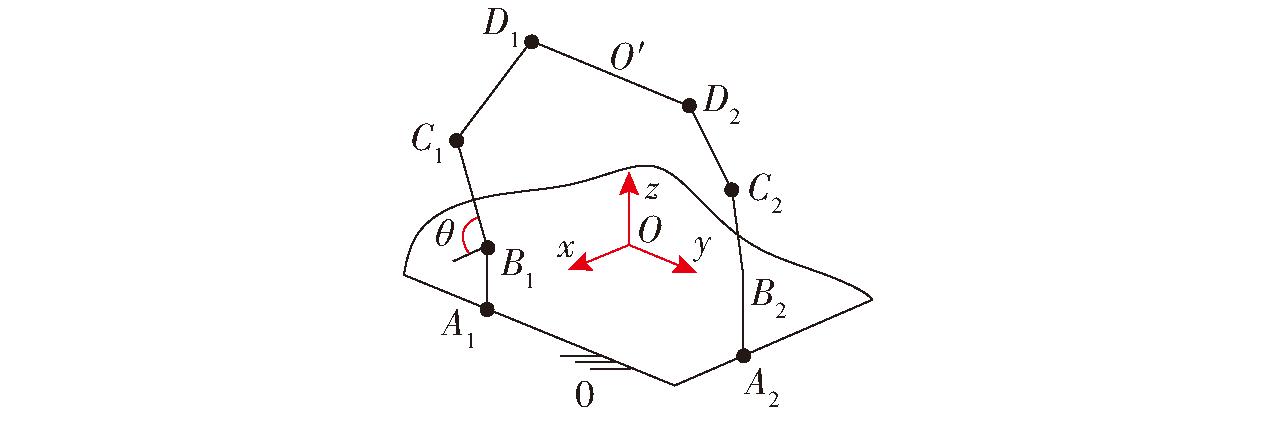
图2 单回路三平移并联机构的运动学模型
Fig.2 Kinematics model of single-loop three-translation PM
(1)位置正解分析
位置正解问题归结为:已知静平台上点A1、A2移动位置分别是yA1、xA2,以及B1C1与x轴正向的夹角是θ,求动平台上O′的坐标(x,y,z)。
易知:A1=(a,yA1,0)、A2=(xA2,b,0)、B1=(a,yA1,l1)、B2=(xA2,b,l2)、C1=(a+l2cosθ,yA1,l1+l2sinθ),且O′=(x,y,z)=(xA2,yA1+d,z),D1=(x,y-d,z)。
由几何约束lC1D1=l3建立位置方程,易得
因此,子并联机构位置正解为
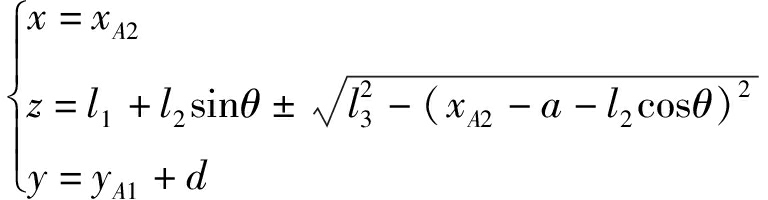
(7)
由式(7)可知,基点O′的x由xA2确定,y由yA1确定,而z仅由θ和xA2两者决定。因此,该机构具有优异的运动解耦性。
(2)位置反解分析
已知动平台1上点O′的坐标为(x,y,z),求静平台上点A1、A2的移动位置yA1、x A2,以及B1C1与x轴正向的夹角θ。
由式(7)得到反解公式为
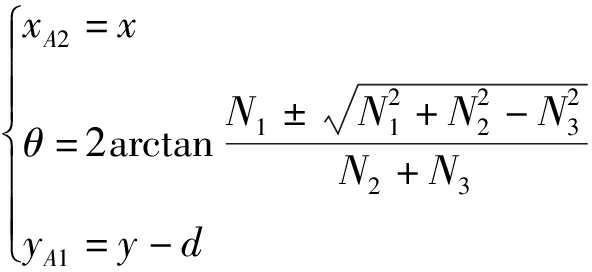
(8)
其中
N1=-2l2(z-l1) N2=-2l2(x-a)
由式(7)、(8)可知,该机构具有很好的符号式正向运动学。
1.2.3 数值验证
设机构杆长:a=280 mm,b=220 mm,l1=120 mm,l2=160 mm,l3=220 mm。
于是,由上述尺寸参数得到机构3D模型,量取3个驱动副yA1、xA1、θ的输入值分别为-135.27 mm、110 mm、120°。
将输入值代入式(7),利用Matlab软件编程,得2个位置正解,分别为:x=110 mm,y=16.73 mm,z=458.85 mm;x=110 mm,y=16.73 mm,z=162.20 mm。两组实数解对应的构型如图3所示。

图3 三平移并联机构构型
Fig.3 Two configurations of three-translation PM
将第1组实数解代入式(8),得到2组反解值,为:xA2=110 mm,yA1=-135.27 mm,θ=π/3;xA2=110 mm,yA1=-135.27 mm,θ=2π/3。
第1组反解与3个输入的测量值一致,因此,验证了位置正解、反解公式正确。
1.2.4 工作空间
采用位置正解计算工作空间,设3个驱动副的输入范围分别为:-500 mm≤xA2≤800 mm、-1 000 mm≤yA1≤1 000 mm、0≤θ≤π。由Matlab对位置正解进行编程,得到工作空间见图4,以及不同x、y、z的截面图如图5所示。
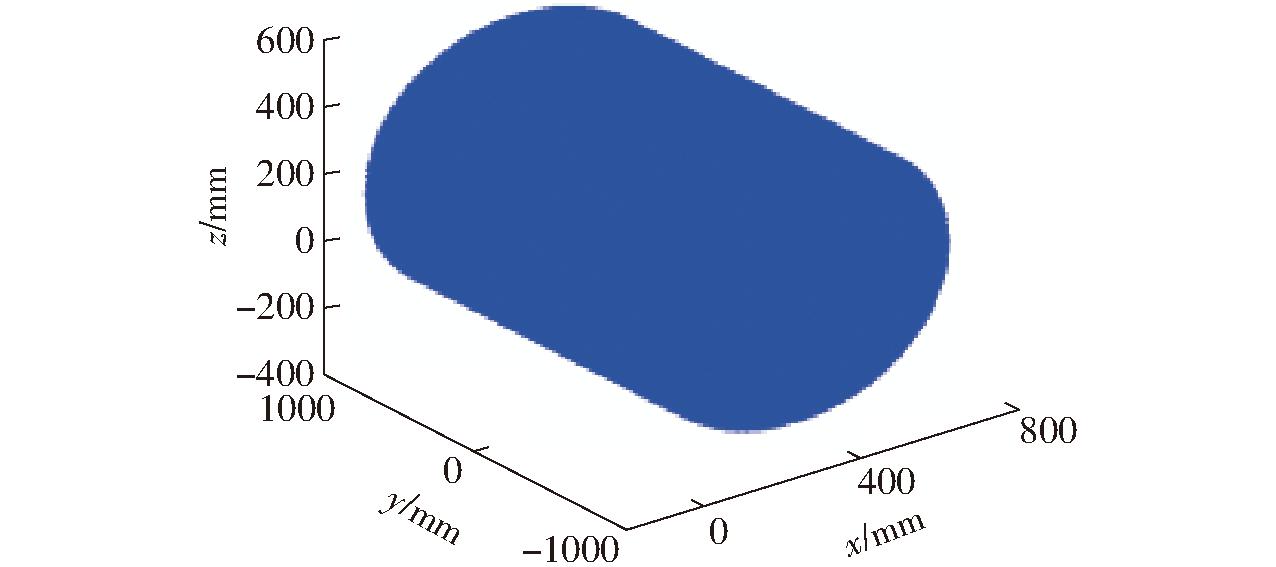
图4 工作空间
Fig.4 Workspace of single-loop PM
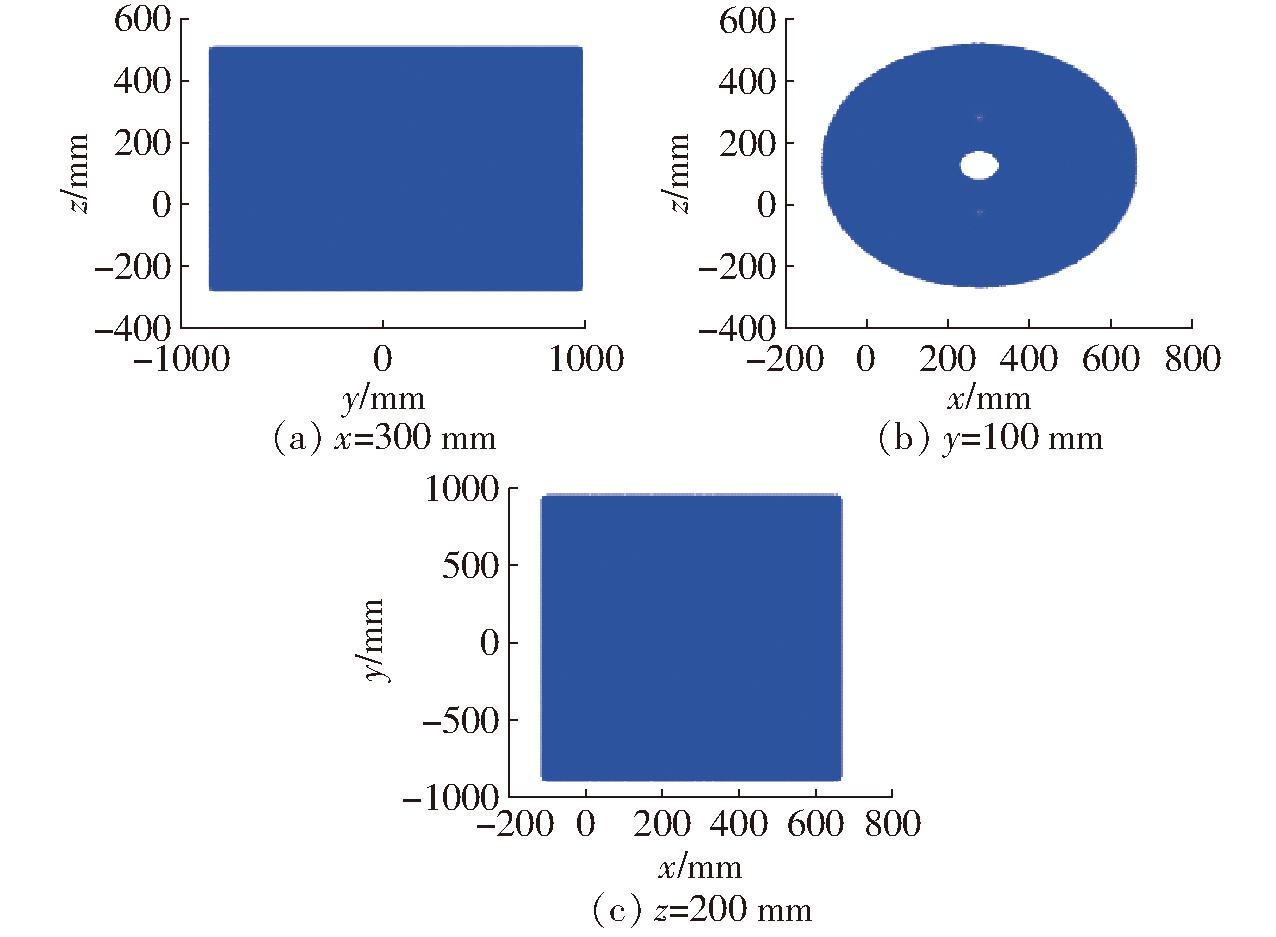
图5 截面图
Fig.5 Cross-section of workspace
1.2.5 奇异性
基于雅可比矩阵的方法进行奇异位形分析,雅可比矩阵为输入关节速度到机构末端输出速度的映射,由于矩阵内部元素与位置有关,因此,在工作空间内部不同位置时,矩阵内部元素也会产生变化,其映射关系为
(9)
式中 Jo——输出雅可比矩阵
Ji——输入雅可比矩阵
![]() 输出元素
输出元素![]() 输入元素
输入元素
根据矩阵Jo和Ji是否奇异,将机构奇异分为3种类型:当det(Ji)=0时,机构发生输入奇异;当det(Jo)=0时,机构发生输出奇异;当det(Ji)=det(Jo)=0时,机构发生综合奇异。
(1)输入奇异
当det(Ji)=0时,机构发生输入奇异,经过分析发现该机构不会发生输入奇异。
(2)输出奇异
当det(Jo)=0时,机构发生输出奇异。由于Jo为下三角矩阵,故机构输出奇异只有一种情况:![]() =f33=0,即D1C1垂直B1C1,如图6所示。
=f33=0,即D1C1垂直B1C1,如图6所示。
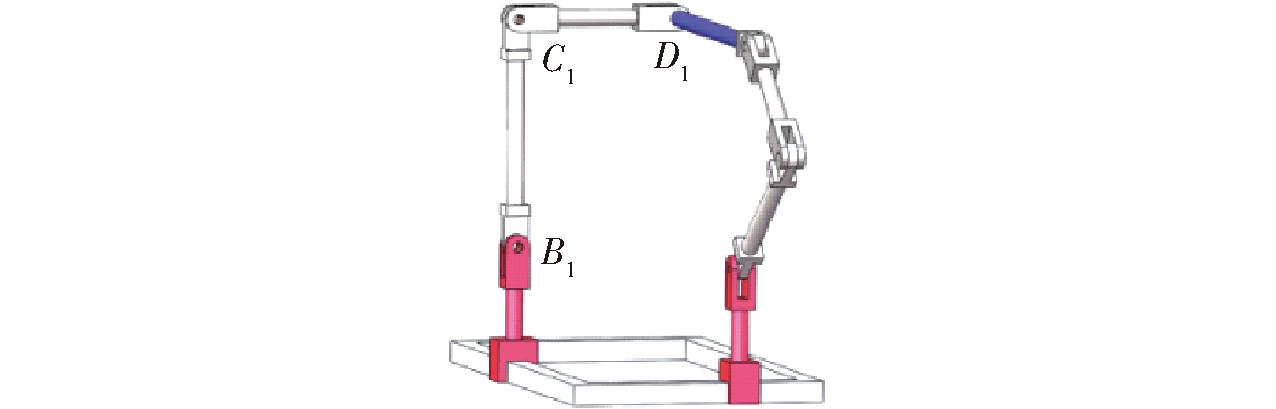
图6 输入奇异位置
Fig.6 Input singular position single-loop PM
(3)综合奇异
当det(Ji)=det(Jo)=0时,机构发生综合奇异。经过分析发现该机构无综合奇异。
以1.2.1节设计的单回路机构为基础,设计一类4个具有运动解耦、正向位置符号化且大工作空间的两回路三平移并联机构,如图7所示,它们均由动平台1、静平台0以及3条支链组成,其中,第Ⅰ、Ⅱ条支链的拓扑结构相同,为SOC{-Pi1‖Ri2‖Ri3‖Ri4-}(i=1,2),它们分别连接动平台1的一、二端;而第Ⅲ条支链有4种不同的情况,具体为:
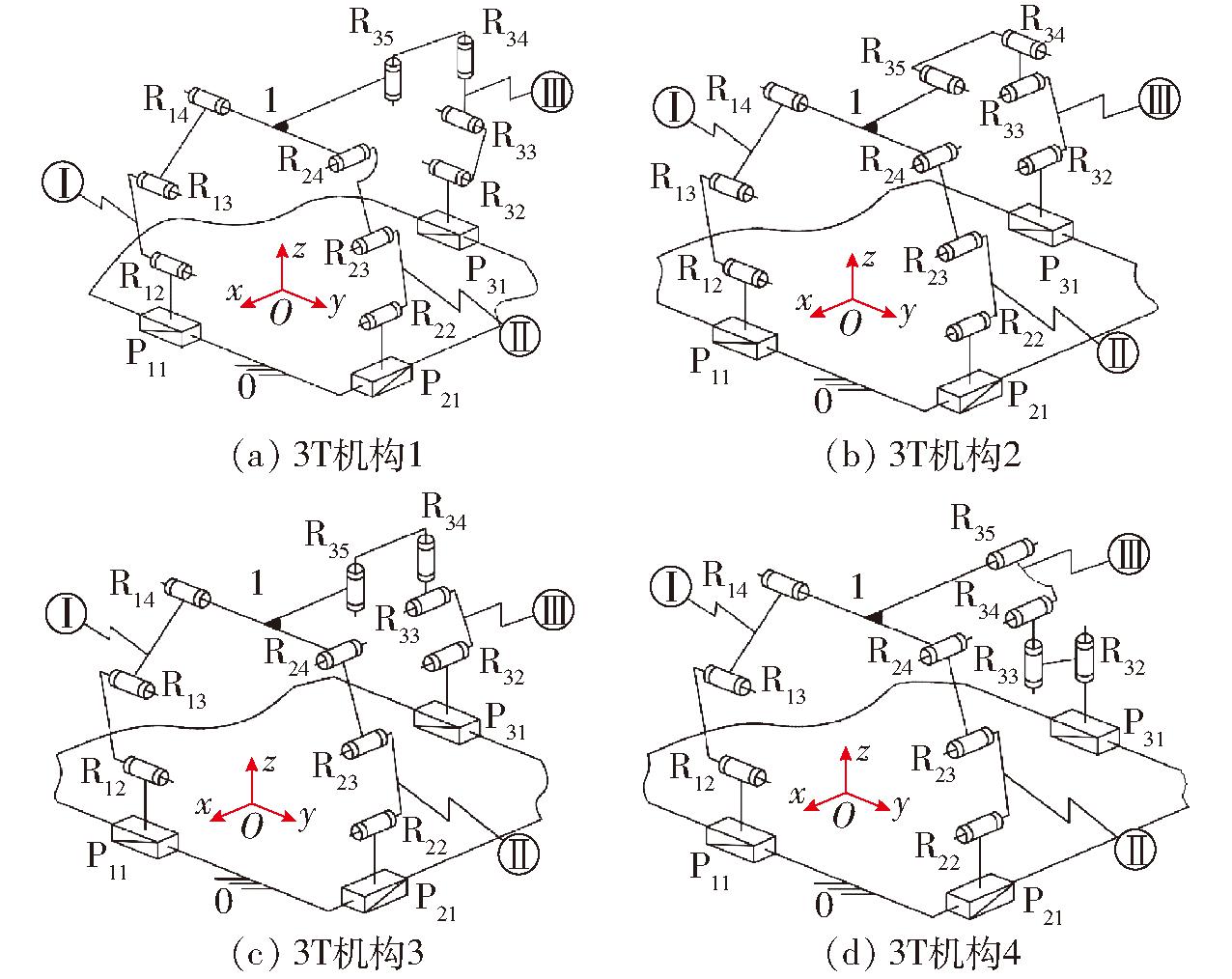
图7 4个两回路的三平移机构
Fig.7 Four two-loop three-translation PMs
(1)由1个移动副(P31)与2个平行轴线的子链1(R32‖R33)连接后,再垂直连接2个平行轴线的子链2(R34‖R35);转动副R35连接动平台1的第3端,且与动平台1其它2端的转动副R14与R24轴线两两垂直,其拓扑结构为SOC{-P31‖R32‖R33⊥R34‖R35},如图7a所示。
(2)由1个移动副(P31)与2个轴线平行的转动副组成的子链1(R32‖R33)、子链2(R34‖R35)串联连接而成,其中,P31⊥R32,R33⊥R34;转动副R35连接动平台1的第3端,且与动平台1其它一端的转动副R14相平行,如图7b所示。
(3)由1个移动副(P31)与2个轴线平行的转动副组成的子链1(R32‖R33)、子链2(R34‖R35)串联连接而成,其中,P31⊥R32,R33⊥R34;而转动副R35连接动平台1的第3端,且与动平台1其它两端的转动副R14与R24轴线两两垂直,如图7c所示。
(4)由1个移动副(P31)与2个轴线平行的转动副组成的子链1(R32‖R33)、子链2(R34‖R35)串联连接而成,且转动副R32的轴线垂直于移动副P31的轴线且在一个运动平面内,而R33⊥R34;转动副R35连接动平台1的第3端,且与动平台1第2端处的转动副R24轴线平行,如图7d所示。
4种情况中,3个P副位于静平台上,且P11‖P31,P11⊥P21。
以图7a所示的三平移机构为例,进行拓扑特性分析。取动平台1上任一点为基点O′,支链Ⅰ、Ⅱ的POC同1.2.1节;支链Ⅲ的POC为
因此,动平台POC集可确定为
第1回路(子并联机构)由第Ⅰ、Ⅱ条支链组成,已求得其独立位移方程数为5,且子动平台POC为3T;第2回路由上述子并联机构和第Ⅲ支链组成,其独立位移方程数为
ξL2=dim(Mb(1-2)∪Mb3)=5
因此,机构的自由度F为
因此,该机构的自由度为3,当取静平台0上的移动副P11、P21、P31为驱动副时,动平台1可实现三平移的运动输出。
第1、2个回路的约束度分别为

显然,第1、2回路组成一个子运动链(SKC),其耦合度κ为
用同样的方法,对余下的图7b~7d所示的3个并联机构进行拓扑分析,可得到相同的拓扑特性(POC、DOF、κ),因此,这4个三平移并联机构将具有相似的运动学、动力学性能。
三平移机构1的运动学模型如图8所示,以矩形静平台几何中心O为原点,建立笛卡尔静坐标系Oxyz,y轴平行于A1、A3所在的导轨,x轴垂直于y轴,z轴由右手定则确定。
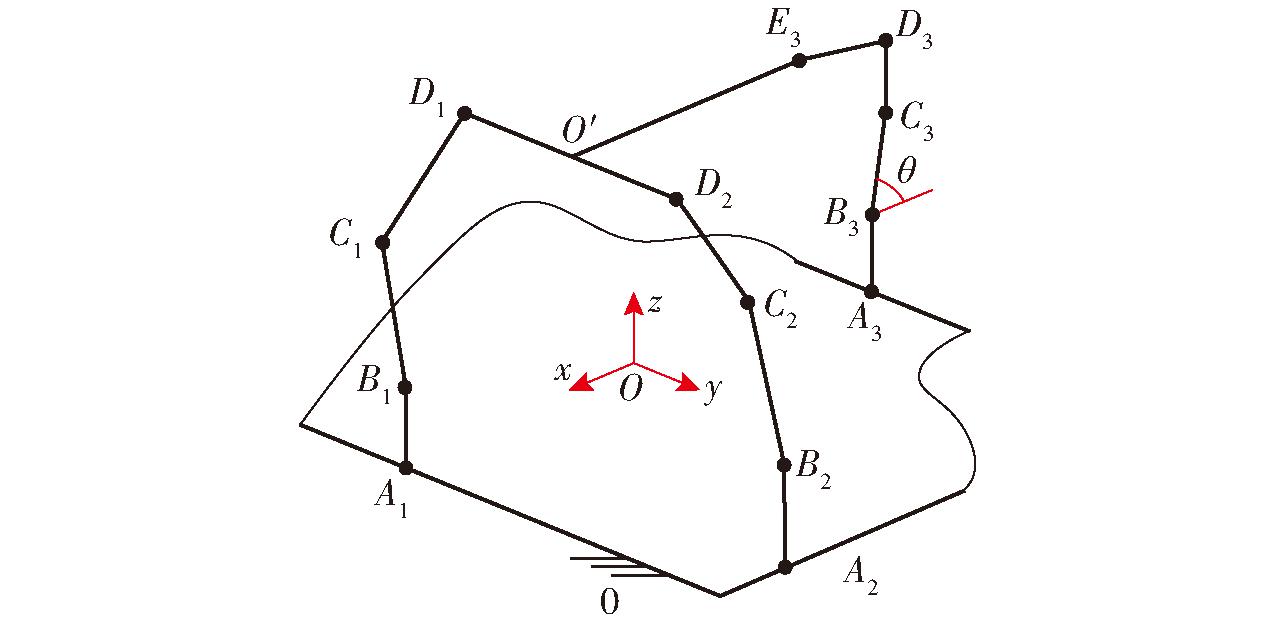
图8 三平移机构1的运动学模型
Fig.8 Kinematics model of three-translation PM 1
设lAiBi=l1(i=1,2,3),lBiCi=l2(i=1,2),lDiCi=l3(i=1,2),lB3C3=l4,lD3C3=l5,lD3E3=l6,A1、A3所在的导轨与原点O的距离均为a,A2所在的导轨与原点O的距离为b,lD1O′=lD2O′ =d,lO′E3=e。
3.1.1 位置正解分析
位置正解问题归结为:已知静平台上3个点Ai(i=1,2,3)的移动位置yA1、x A2、yA3,求动平台1上O′=(x,y,z)。
易知,A1=(a,yA1,0)、A2=(xA2,b,0)、A3=(-a,yA3,0);B1=(a,yA1,l1)、B2=(xA2,b,l1)、B3=(-a,yA3,l1)。
设O′=(x,y,z)中的垂直分量为z*,C3B3与x轴负向夹角为θ。
(1)第1回路(A1-B1-C1-D1-D2-C2-B2-A2)的求解
由动平台三平移特性,求得
O′=(x,y,z)=(xA2,yA1+d,z*)
(2)第2回路(O′-E3-D3-C3-B3-A3)的求解
由O′、B3、C3点坐标,分别可以得出
E3=(x-e,y,z)
C3=(-a-l4cosθ,yA3,l1+l4sinθ)
D3=(-a-l4cosθ,yA3,l1+l4sinθ+l5)
因E3与D3位于同一高度,所以zE3=zD3,可得
z=l1+l5+l4sinθ
(10)
由几何约束E3D3=l6建立的位置方程,解得θ为
其中 N3=e-a-xA2 N4=yA1+d-yA3
因此,机构位置正解为
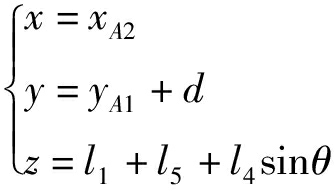
(11)
由式(11)可知,该3T机构不仅有符号式位置正解,且点O′的x值由xA2确定,y值由yA1确定,而z由xA2、yA1、yA3三者共同确定,因而具有较好的I-O运动解耦性。
3.1.2 位置反解分析
已知动平台上点O′的坐标(x,y,z),求3个移动副输入值,即ρ=(xA2,yA1,yA3)。
由式(10)可得
因此,由式(11)求得反解方程为
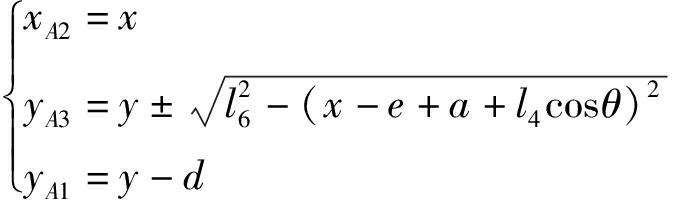
(12)
3.1.3 正逆解数值验算
取机构杆长为:a=280 mm,b=220 mm,d=152 mm,e=300 mm,l1=120 mm,l2=220 mm,l3=160 mm,l4=180 mm,l5=125 mm,l6=160 mm。
由上述尺寸得到机构的3D模型,取3个驱动副P11、P21、P31输入值分别为yA1=-144.36 mm、xA2=94.25 mm、yA3=-47.68 mm。
将输入值代入正解式(11),利用Matlab,得到2个位置正解,其中,1组实数解为:x=94.25 mm,y=7.64 mm,z=408.223 4 mm。该实数解对应的构型如图9所示。
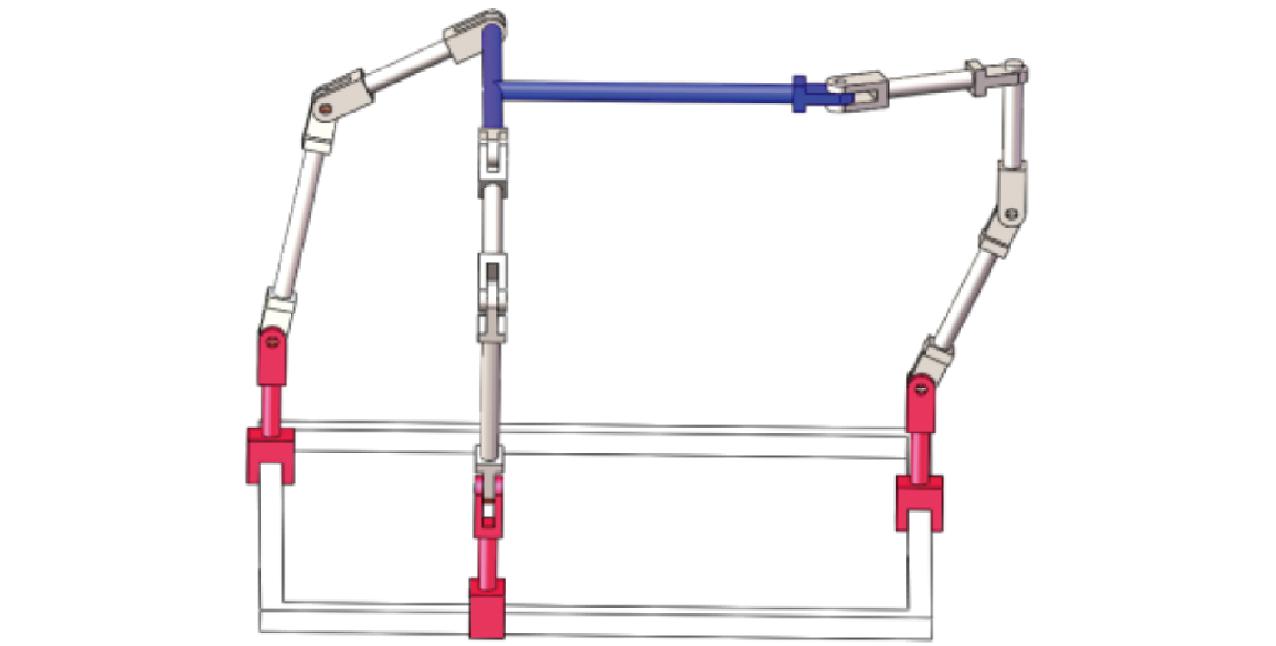
图9 对应于正解的机构构型图
Fig.9 Configuration diagram for forward solution
将此实数解代入式(12),得到2组反解值:yA1=-144.36 mm,xA2=94.25 mm,yA3=-47.68 mm;yA1=-144.36 mm,xA2=94.25 mm,yA3=62.959 9 mm。
第1组反解与3个输入的测量值一致,因此,正、反解公式的正确性得到验证。
3.2.1 动平台速度
对位置反解方程(12)进行全微分,可得
(13)
其中
![]()
![]()
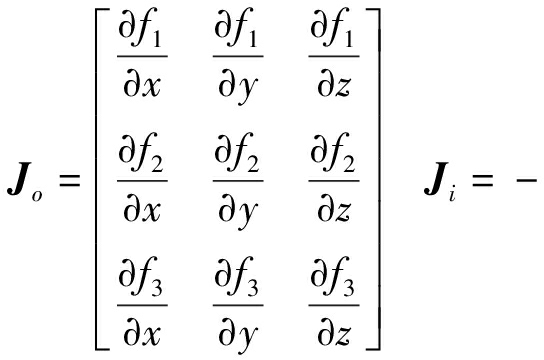
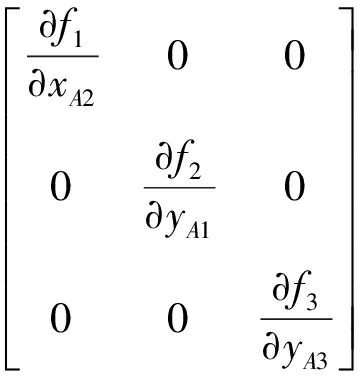
![]()
![]()
![]()
(x-e+a+l4cosθ)
![]()
![]()
(x-e+a+l4cosθ)sinθ·
![]()
![]()
![]()
当机构不处于奇异位形时,Jo可逆,则
(14)
式(14)即为动平台1上点O′的速度映射模型。
3.2.2 加速度
将式(14)两边同时对时间t求导,当机构不处于奇异位形时,Jo可逆,并整理得
(15)
其中
而Ki(i=1,2,3)为矩阵Jo和Ji中元素fij(i=1,2,3;j=1,2,3)对时间t的导数与对应变量对时间t的导数的乘积之和,即
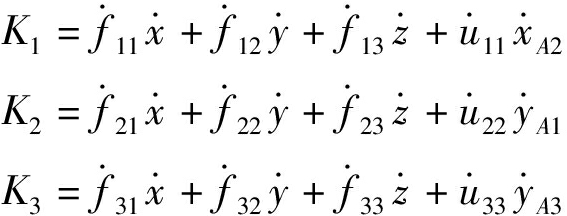
式(15)即为动平台上点O′的加速度映射模型。由Matlab编程和Solidworks仿真,可得式(14)、(15)正确。
(1)输入奇异
当det(Ji)=0时,机构发生输入奇异,由上述可知机构不会发生输入奇异。
(2)输出奇异
当det(Jo)=0时,机构发生输出奇异。由于Jo为下三角矩阵,故机构输出奇异只有一种情况
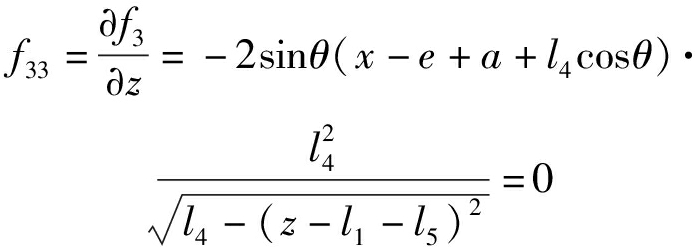
当sinθ=0时,D3C3垂直于B3C3,如图10a所示。
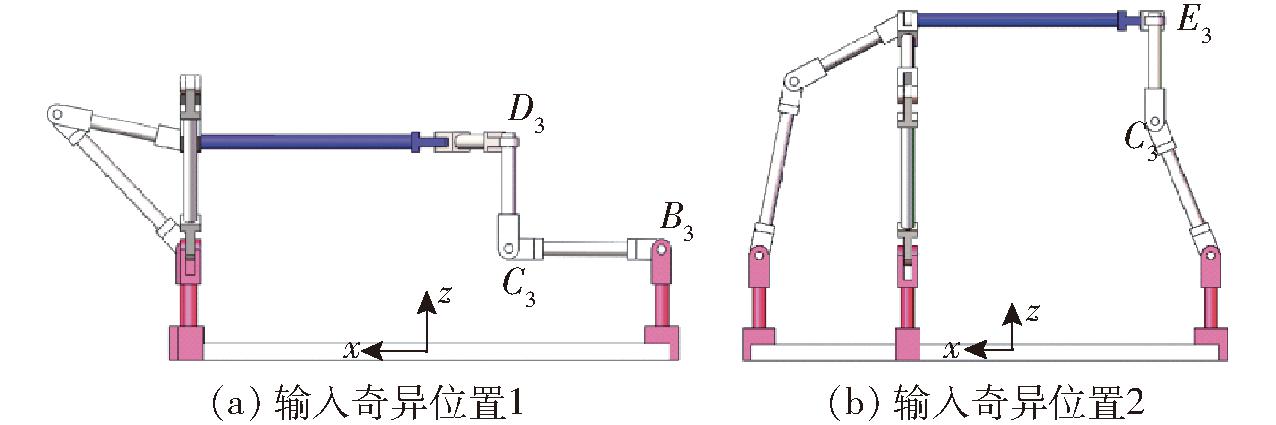
图10 机构1输入奇异位置
Fig.10 Input singular position
当x-e+a+l4cosθ=0时,点E3与点C3的x轴坐标相等,如图10b所示。
(3)综合奇异
当det(Ji)=det(Jo)=0时,机构发生综合奇异。经过分析发现该机构无综合奇异。
采用位置正解计算工作空间,设3个驱动副输入范围分别为:-500 mm≤xA2≤600 mm、-1 000 mm≤yA1≤1 000 mm、-500 mm≤yA3≤500 mm。
利用Matlab,对位置正解式(11)进行编程,得到工作空间如图11所示,以及不同x、y、z值的截面图,如图12所示。由图11、12可知,该机构具有较大的、近似矩形的有效工作空间。
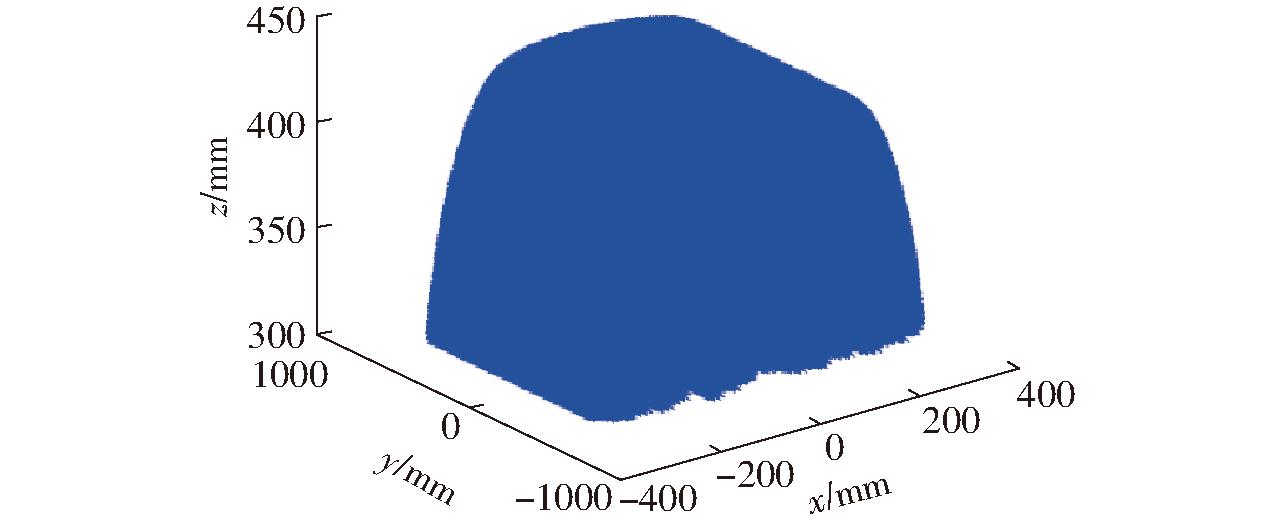
图11 3T机构工作空间
Fig.11 Workspace for 3T PM
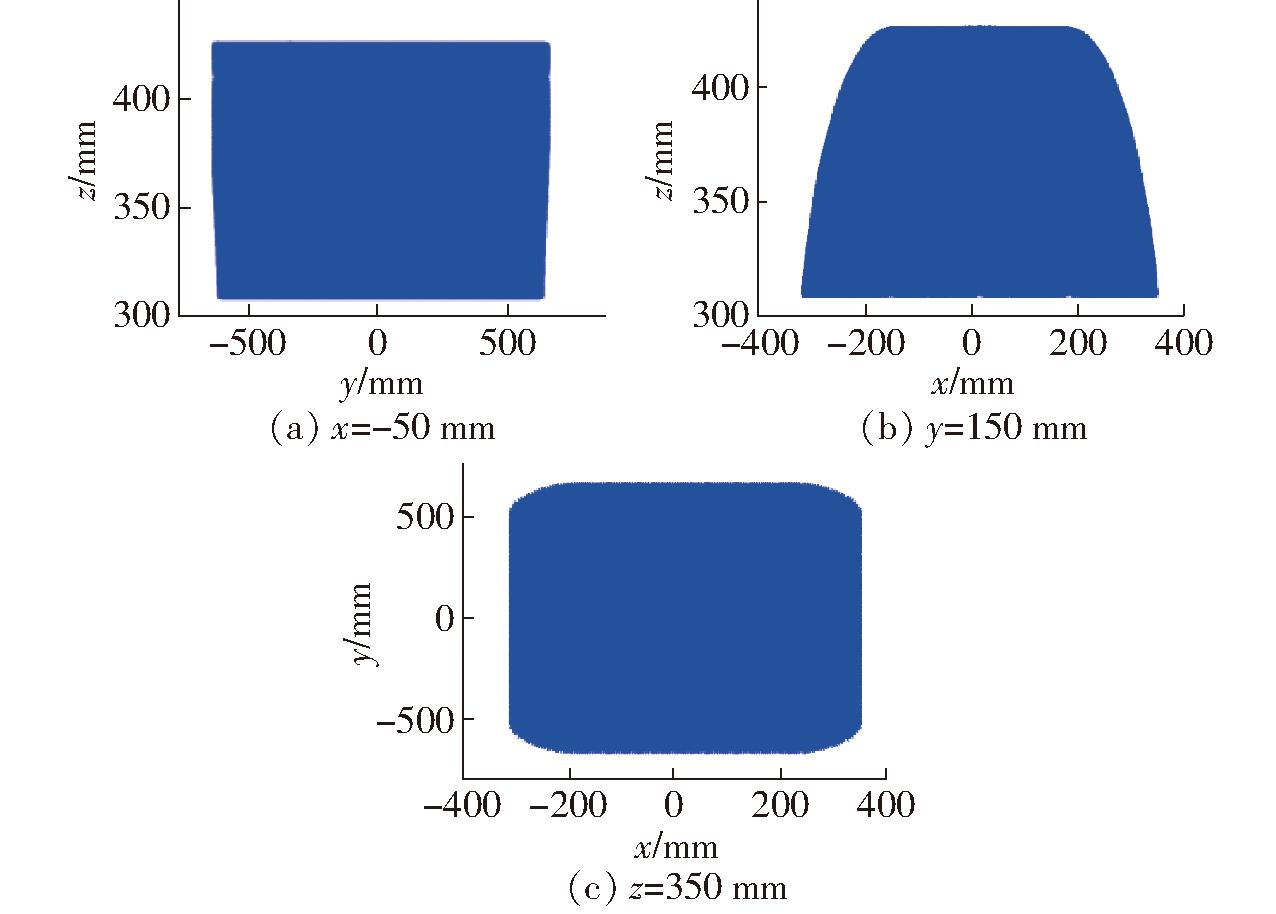
图12 机构1截面图
Fig.12 Cross-section of workspace
同样,这类机构具有相似的大工作空间,是指这类机构的工作空间呈立方体形状,其xOy截面的面积由两边长x、y决定,其中,边长y的值由滑块P11的位移线性决定,边长x的值由滑块P21的位移线性决定,而z方向由3个滑块P11、P21、P31 共同决定。因此,只要滑块P11、P21的驱动范围足够大,xOy截面的截面积就足够大,因而其整个的立方体工作空间也很大。
而其他大多数三平移并联机构工作空间的xOy截面面积不具备这样的数值特征,即截面的两边长不能由两驱动滑块位移线性决定。因此,认为这类机构具有大工作空间。
4.1.1 SKC2内各杆件
(1)动平台
取动平台质心为点O′,则
(16)
式中 fO′——动平台所受外力
τO′——动平台所受外力矩
mO′——动平台质量
g——重力加速度
ω1——动平台角速度
ε1——动平台角加速度
IO′——坐标系Oxyz下动平台惯量矩阵
FO′——动平台所受的力
MO′——动平台所受力矩
(2)移动滑块A3B3
(17)
其中
式中 mA3B3——滑块A3B3质量
fA3B3——滑块A3B3上的驱动力
(3)转动杆B3C3
(18)
式中 mB3C3——杆B3C3质量
IB3C3——坐标系Oxyz下杆B3C3惯量矩阵
(4)转动杆C3D3
(19)
式中 mC3D3——杆C3D3质量
IC3D3——坐标系Oxyz下杆C3D3惯量矩阵
(5)转动杆D3E3
(20)
式中 mD3E3——杆D3E3质量
ID3E3——坐标系Oxyz下杆D3E3的惯量矩阵
(6)转动杆E3O′
(21)
式中 mE3O′——杆E3O′质量
IE3O′——坐标系Oxyz下杆E3O′惯量矩阵
4.1.2 SKC1内各杆件
(1)杆件D1D2
由于杆件D1O′和D2O′同轴线,不发生相对转动,故将杆件D1O′和D2O′ 视为同一杆件D1D2,可得
(22)
式中 mD1D2——杆D1O′和D2O′总质量
(2)驱动滑块AiBi
![]()
(i=1,2)
(23)
式中 mAiBi——滑块AiBi质量
fAiBi——滑块AiBi上的驱动力
(3)杆件BiCi
![]()
![]()
(i=1,2)
(24)
式中 mBiCi——杆BiCi质量
IBiCi——坐标系Oxyz下杆BiCi惯量矩阵
(4)杆件CiDi
![]()
![]()
(i=1,2)
(25)
式中 mCiDi——杆CiDi质量
ICiDi——坐标系Oxyz下杆CiDi惯量矩阵
SKC2动力学方程为
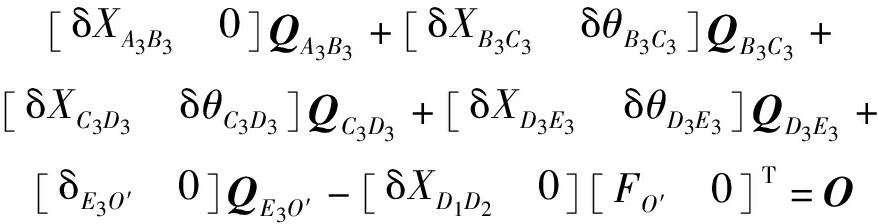
(26)
SKC1动力学方程为
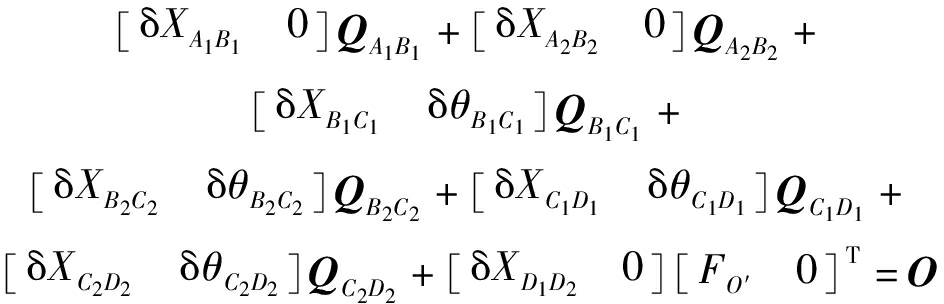
(27)
其中
δXAiBi=JvAiBiδq (i=1,2,3)
δXBiCi=JvBiCiδq (i=1,2)
δXB3C3=JvB3C3δq δXCiDi=JvCiDiδq (i=1,2,3)
δXD3E3=JvD3E3δq δXD1D2=JvD1D2δq
δXE3O′=JvE3O′δq
δθBiCi=JωBiCiδq (i=1,2)
δθB3C3=JωB3C3δq
δθCiDi=JωCiDiδq (i=1,2,3)
δθD3E3=JωD3E3δq
假设取3个驱动副P11、P21、P31的输入函数均为:y=10sin(0.5t);各杆件质量为:mAiBi=4.53 kg,mB1C1=4.04 kg,mB2C2=4.04 kg,mB3C3=3.47 kg,mC1D1=3.67 kg,mC2D2=3.67 kg,mC3D3=2.53 kg,mD3E3=3.43 kg,mMO′=9.2 kg。
各杆件转动惯量如表1所示。
表1 各杆件转动惯量
Tab.1 Moment of inertia parameters of each link kg·mm2
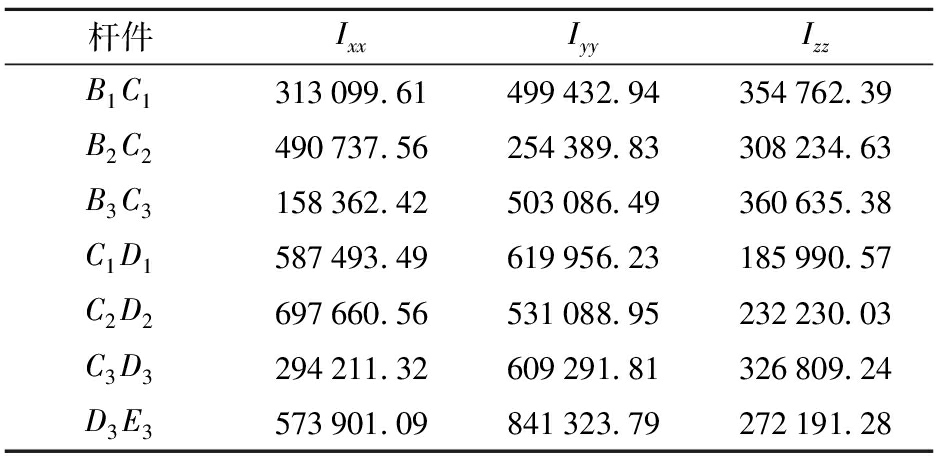
杆件IxxIyyIzzB1C1313099.61499432.94354762.39B2C2490737.56254389.83308234.63B3C3158362.42503086.49360635.38C1D1587493.49619956.23185990.57C2D2697660.56531088.95232230.03C3D3294211.32609291.81326809.24D3E3573901.09841323.79272191.28
将以上参数代入动力学方程式(16)~(27),设负载为10 kg,运用Matlab计算该机构驱动力;同时,将虚拟样机导入ADAMS中进行仿真得到3个滑块的驱动力曲线,如图13所示。
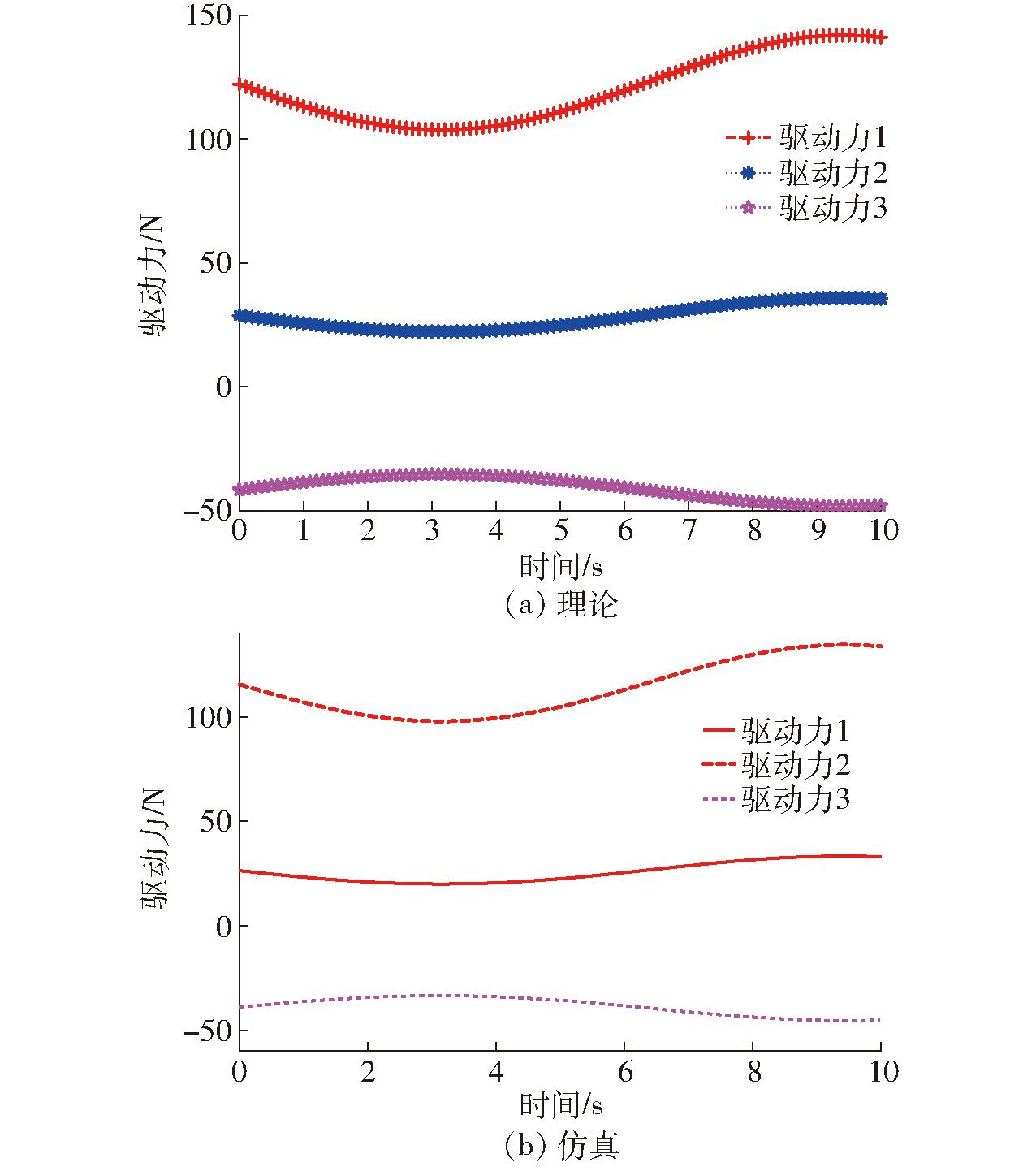
图13 驱动力曲线
Fig.13 Actuated force curves of 3T PM
由图13可知,驱动力理论曲线与仿真曲线一致,仅存在细微误差,故动力学模型正确;同时,表明3个滑块所需的最大驱动力为142.2 N,从而为该机构驱动电机的选择奠定了技术基础。
(1)提出了一种运动解耦且符号式位置正解的单回路三平移并联机构,设计一类4种全由低副组成、制造方便,同时具有符号式位置正解且部分运动解耦、大工作空间的三平移并联机构,这些特性有利于对这类机构进行实时控制。
(2)以其中一个机构为例,进行了速度、加速度、奇异性和工作空间分析,得到了各杆件速度雅可比矩阵。
(3)根据基于虚功原理的序单开链法,建立了该机构的动力学模型,并利用ADAMS软件对虚拟样机进行了仿真,证明了该动力学模型的正确。
[1] CLAVEL R.A fast robot with parallel geometry[C]∥Proceedings of the 18th Int.Symposium on Industrial Robots,1988:91-100.
[2] KELAIAIA R,COMPANY O,ZAATRI A.Multiobjective optimization of a linear Delta parallel robot[J].Mechanism & Machine Theory,2012,50(2):159-178.
[3] 程强.3P-Delta并联机构的参数优化与轨迹规划[D].太原:中北大学,2017.
CHENG Qiang.Parameter optimization and trajectory planning of 3P-Delta parallel mechanism[D].Taiyuan:North University of China,2017.(in Chinese)
[4] TSAI L W,JOSHI S.Kinematics and optimization of a spatial 3-UPU parallel manipulator ASME[J].Mech.Des.,2000,122:439-446.
[5] BOURI M,CLAVEL R.The linear Delta:developments and applications[C]∥Robotics,VDE,2010:1-8.
[6] 刘延斌,底复龑.一种新型3-RRRU并联机构及其运动学分析[J].中国机械工程,2013,24(4):476-481.
LIU Yanbin,DI Fuyan.A novel 3-RRRU parallel mechanism and its kinematics analysis[J].China Mechanical Engineering,2013,24(4):476-481.(in Chinese)
[7] LI Y,XU Q.Kinematic analysis and design of a new 3-DOF translational parallel manipulator[J].ASME.J.Mech.Des.,2006,128(4):729-737.
[8] WANG X,BARON L,ClOUTIER G.Topological and geometrical synthesis of three-degree-of-freedom fully parallel manipulators by instantaneous kinematics[J].ASME.J.Mech.Des.,2008,130(3):032301.
[9] DI GREGORIO R,PARENTI-CASTELLI V.Mobility analysis of the 3-UPU parallel mechanism assembled for a pure translational motion[J].ASME.J.Mech.Des.,2002,124(2):259-264.
[10] DI GREGORIO R.Kinematics of the translational 3-URC mechanism[J].ASME.J.Mech.Des.,2004,126(6):1113-1117.
[11] 郭宗和,马履中,尹小琴,等.非对称三平移并联机构的运动条件设计[J].农业机械学报,2006,37(10):112-115.
GUO Zonghe,MA Lüzhong,YIN Xiaoqin,et al.Design of kinematic conditions for an asymmetric three-translation parallel mechanism[J].Transactions of the Chinese Society for Agricultural Machinery,2006,37(10):112-115.(in Chinese)
[12] 李丽红,张发海,朱磊.2-CPR/UPU三平移并联机构运动学分析与优化设计[J].机械传动,2022,46(10):64-70,76.
LI Lihong,ZHANG Fahai,ZHU Lei.Kinematics analysis and optimal design of 2-CPR/UPU three-translation parallel mechanism[J].Journal of Mechanical Transmission,2002,46(10):64-70,76.(in Chinese)
[13] 李菊,肖思进,沈惠平,等.两支链三平移并联机构动力学分析与性能优化[J].农业机械学报,2022,53(10):412-422,445.
LI Ju,XIAO Sijin,SHEN Huiping,et al.Dynamic analysis and performance optimization of two-chain three-translation parallel mechanism[J].Transactions of the Chinese Journal for Agricultural Machinery,2022,53(10):412-422,445.(in Chinese)
[14] 李菊,朱忠颀,沈惠平,等.三平移并联机构拓扑设计与运动学分析[J].农业机械学报,2022,53(9):425-433,442.
LI Ju,ZHU Zhongqi,SHEN Huiping,et al.Topological design and kinematic analysis of three-translation parallel mechanism[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(9):425-433,442.(in Chinese)
[15] 曾达幸,李晓帆,邱雪松,等.新型三平移解耦并联机构的综合[J].中国机械工程,2015,26(10):1279-1283.
ZENG Daxing,LI Xiaofan,QIU Xuesong,et al.Synthesis of a novel three-level transfer decoupled parallel mechanism[J].China Mechanical Engineering,2015,26(10):1279-1283.(in Chinese)
[16] 马履中,郭宗和,杨启志,等.三平移弱耦合并联机器人机构精度分析[J].江苏大学学报(自然科学版),2005,26(3):198-202.
MA Lüzhong,GUO Zonghe,YANG Qizhi,et al.Precision analysis of three-translation weakly coupled parallel robot mechanism[J].Journal of Jiangsu University (Natural Science Edition),2005,26(3):198-202.(in Chinese)
[17] 谢俊,左飞飞,杨启志,等.一种三自由度弱耦合并联机构运动学分析[J].机床与液压,2022,50(1):36-43.
XIE Jun,ZUO Feifei,YANG Qizhi,et al.Kinematics analysis of a three-degree-of-freedom weakly coupled parallel mechanism[J].Machine Tool &Hydraulics,2022,50(1):36-43.(in Chinese)
[18] 沈惠平,吴成琦,许可,等.一种零耦合度三平移并联机构的设计及运动学[J].中国机械工程,2019,30(6):658-664,671.
SHEN Huiping,WU Chengqi,XU Ke,et al.Design and kinematics of a zero-coupling three-translation parallel mechanism[J].China Mechanical Engineering,2019,30(6):658-664,671.(in Chinese)
[19] 沈惠平,吉昊,许正骁,等.三平移机构设计与运动学符号解及性能评价[J].农业机械学报,2020,51(9):397-407.
SHEN Huiping,JI Hao,XU Zhengxiao,et al.Design kinematic symbolic solution and performance evaluation of three-translation mechanism[J].Transactions of the Chinese Society for Agricultural Machinery,2019,51(9):397-407.(in Chinese)
[20] 赵一楠,沈惠平,陆晨芳,等.基于SKC的新型3T并联机构的运动学、奇异性和工作空间分析[J].机械传动,2023,47(7):58-68.
ZHAO Yi’nan,SHEN Huiping,LU Chenfang,et al.Kinematics,singularity and workspace analysis of a novel 3T parallel mechanism based on SKC[J].Journal of Mechanical Transmission,2023,47(7):58-68.(in Chinese)
[21] 梁栋,刘军,畅博彦,等.末端铰接三平动并联机构设计与性能优化[J].农业机械学报,2022,53(10):446-458.
LIANG Dong,LIU Jun,CHANG Boyan,et al.Design and performance optimization of three-translational parallel mechanism with articulated end[J].Transactions of the Chinese Society for Agricultural Machinery,2022,53(10):446-458.(in Chinese)
[22] 李丽红,张发海,朱磊.2-CPR/UPU三平移并联机构运动学分析与优化设计[J].机械传动,2022,46(10):64-70,76.
LI Lihong,ZHANG Fahai,ZHU Lei.Kinematic analysis and optimal design of 2-CPR/UPU three-translation parallel mechanism[J].Journal of Mechanical Transmission,2012,46(10):64-70,76.(in Chinese)
[23] 彭红梅,陈亚,陆彩满,等.新型三平移2PPPa并联机构运动学分析与优化设计[J].机床与液压,2022,50(3):43-48.
PENG Hongmei,CHEN Ya,LU Caiman,et al.Kinematics analysis and optimal design of a new three-translation 2PPPa parallel mechanism[J].Machine Tool &Hydraulics,2022,50(3):43-48.(in Chinese)
[24] 杨廷力,刘安心,罗玉峰,等.机器人机构拓扑结构设计[M].北京:科学出版社,2012.
[25] 沈惠平.机器人机构拓扑特征运动学[M].北京:高等教育出版社,2021.