并联机器人运动轨迹规划并联机器人运动轨迹规划OSID：
Parallel Robot Based on 345-Corrected Trapezoidal Motion Law在众多工业机器人中,存在一种由外转动驱动、含平行四边形支链的高速并联机器人,由于其驱动器可布置在机架上,从动臂可设计制作成轻杆,故末端执行器在工作过程中可获得很高的速度和加速度,特别适合智能高速物流生产线上轻散小物料的分拣、搬运和抓放等作业,已在众多领域自动化生产线上得到广泛的应用[1]。典型的并联机器人有H4、I4、Heli4和Par4等[2-5]。
高速抓放操作要求并联机器人末端以高速度和高加速度运动,如果机构末端运动函数和轨迹路径选择不恰当,机构运动过程将出现位置、速度和加速度突变,导致机构运动不平稳,引起抓放操作过程中的冲击,影响抓放操作质量甚至是缩减并联机器人的使用寿命,然而单纯地追求轨迹平滑又会降低效率。轨迹规划可找出兼顾两者的最优解,故是该类机构运动控制开发的重要环节。
目前提高轨迹规划运动效率有两种方式:运动规律优化和轨迹路径优化[6-11]。一方面,常用的运动规律有正弦加速度、修正梯形加速度和3-4-5次多项式等[12]。其中3-4-5次多项式是一种在轨迹规划中应用较广的运动规律,能保证运动过程中位移、速度、加速度连续,提升运动平稳性,但是由于它不能短时间内达到加速度峰值,将速度快速提升至最高,因此降低了运行效率,而梯形运动规律因为加速度恒定,所以能在最短的时间达到目标位置,但始末位置加速度突变,对电机冲击较大,末端运动平稳性较差。另一方面,高速并联机器人的轨迹通常是门形轨迹。优化门形轨迹中直角转角部分是优化的关键。到目前为止,已经有许多种优化门形轨迹直角部分的方法被提出来,例如三次多项式曲线的使用[13],可以使其关节轨迹曲线比椭圆轨迹更平滑,但具有冲击曲线突变的缺点;借助五次多项式曲线[14]和Lamé曲线(超椭圆曲线)[15]可摒除向心加速度突变的情况并且有效地减少震动,然而其路径插补点计算复杂,对工控机的要求高;为简化离散点计算和减少硬件成本,CHEN等[16]使用B样条曲线设计了上平台运动轨迹;使用螺旋圆曲线[17]也可以避免门形轨迹中法向加速度的突变,但是运动规律的选择将会受到限制;GUO等[18]应用PH曲线过渡轨迹的直角部分,以降低机器人端部的峰值速度,但未考虑对主动臂状态的影响。由此可见,现有的研究多为对轨迹路径的考虑,或只在末端对多个运动规律进行比较优选,而未考虑末端运动规律和运动轨迹对主动臂关节运动的影响。
本文以一种新型4自由度高速并联机器人为对象[19],建立其运动学模型,从运动函数优化和轨迹路径优化两方面入手,结合3-4-5次多项式和梯形运动规律的优点,提出一种在额定加速度条件下,通过融合3-4-5次多项式运动规律和梯形运动规律,以期在提高运动效率的同时,改善加速度突变问题;并着重考虑主动臂的运动状态研究机器人运动轨迹规划问题,以期兼顾高速并联机器人抓放的稳定性和快速性。
图1为
四自由度高速并联机器人机构的三维模型。该机构主要包括静平台、动平台以及连接静、动平台结构相同的4条支链。
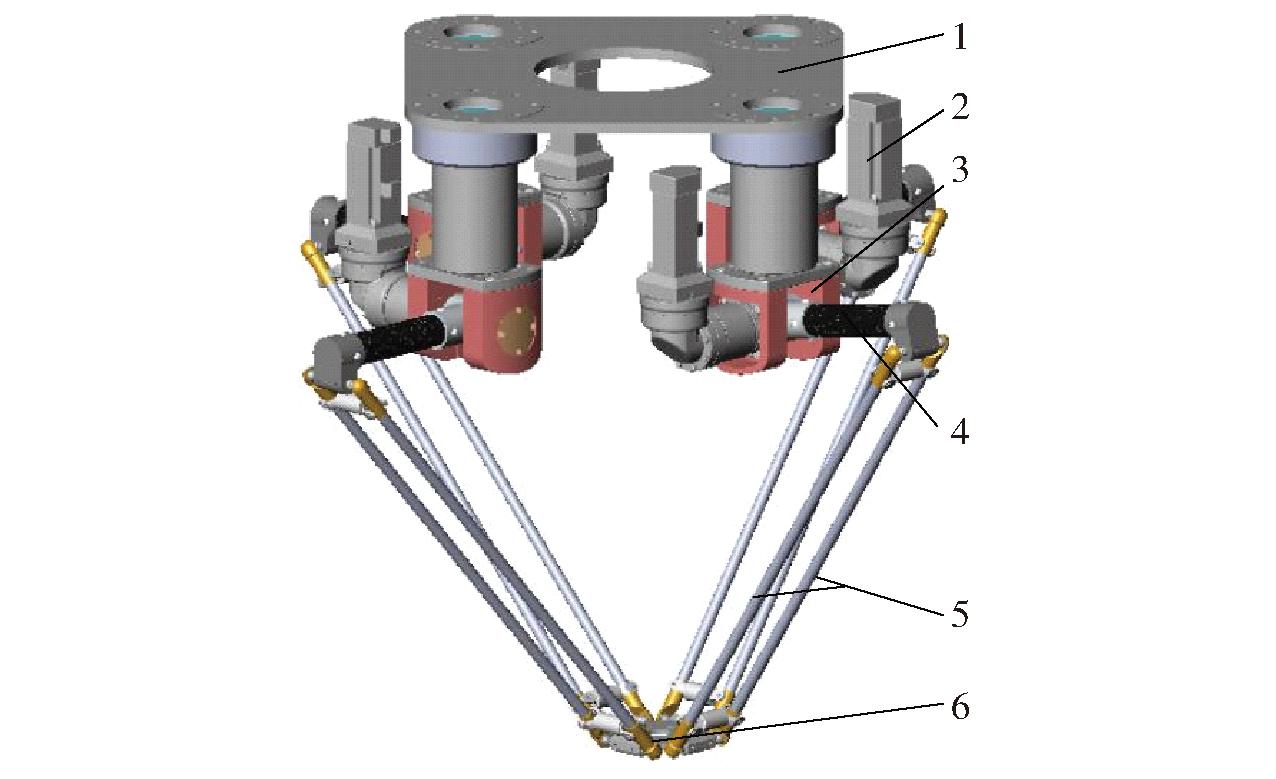
图1 
高速并联机器人机构三维模型
Fig.1 Model of high-speed parallel robot
1.静平台 2.伺服电动机 3.转动叉 4.主动臂 5.从动臂 6.动平台
每条支链均由转动叉、主动臂和含平行四边形的从动臂组成,其连接方式为
其中R表示转动副,
表示主动转动副,(SS)2表示两端都是球副的平行四边形结构。因为以
为拓扑结构的支链内含三维平动,所以在此基础上,每条支链通过转动叉与静平台转动连接,即每条支链均添加一个转动副,最终该机构拥有三平移一转动的自由度。为提供绕竖直轴转动的转动力矩,将4条支链设计为偏置结构,并将动平台设计为非正方形结构。本机器人因为采用单动平台结构,所以可有效减轻运动部件质量,从而对机器人高速度和高加速度动态特性有较大提升。
机构简图如图2所示,图中点P′i和点A′i (i=1,2,3,4)分别为支链i与动、静平台连接的铰链中心,点Bi为连接主动臂和从动臂的铰链中心,Ai和Pi为A′i和P′i支链偏置前的位置。以静平台几何中心点为原点建立固定参考坐标系Oxyz,其中x轴方向由点O指向点A1,z⊥A1A2A3A4,y轴满足右手定则。在初始位型下,点A′1和A′3上的R转动副轴线经过偏置安装后依然与y轴平行,点A′2和A′4上的R转动副轴线经过偏置安装后依然与x轴平行。以动平台几何中心点为原点构建动平台连体坐标系O′x′y′z′,其中x′轴方向由点O′指向点P1,z′⊥P1P2P3P4,y′轴满足右手定则。为描述方便,在此,记ζ1为动平台结构角,即
和
间的钝角;记ζ2和ζ3分别为动、静平台装配偏置角,即分别为
和
和
的锐角。
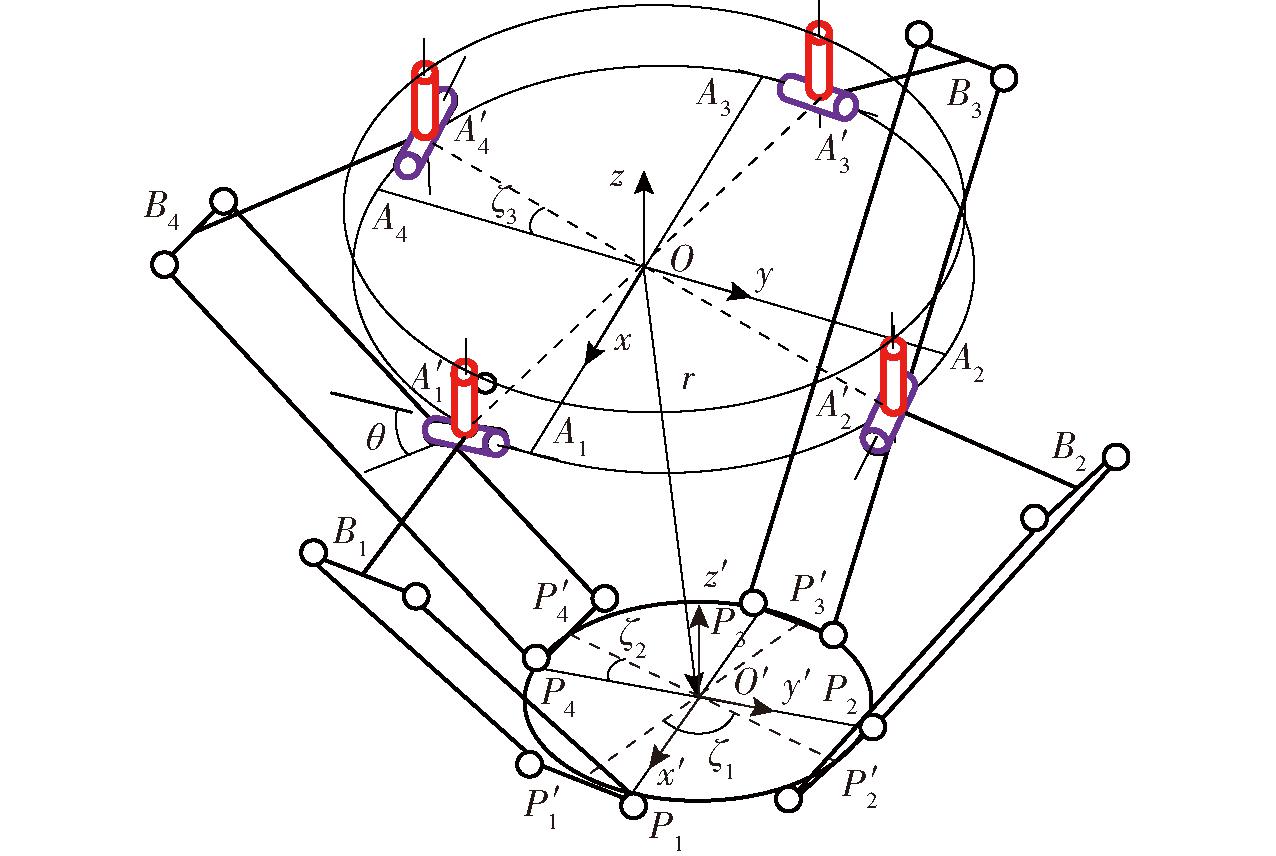
图2 机构简图
Fig.2 Mechanism diagram
如图2所示,并联机器人末端动平台中心参考点O′在参考坐标系Oxyz中的位置矢量r可表示为
r=ai+L1ui+L2wi-pi i=(1,2,3,4)
(1)
对式(1)分别求一阶导和二阶导,可得
(2)
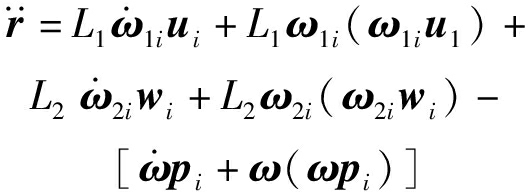
(3)
其中
γi=(i-1)π/2
βi=(i-1-εi)π/2+εiζ1+ζ2+θ
式中 L1、L2——主、从动臂杆长
ai、pi——由点O到点A′i和点O′到点P′i的位置矢量
ui、wi——主、从动臂单位方向矢量
R1、R2——动、静平台半径
αi——主动臂转角
γi——A′i方位角
θ——机构运动时绕z轴的转角
点O′线速度
ω1i、ω2i——主、从动臂角速度
转动叉绕垂直轴角速度
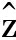——z轴单位方向矢量
主动臂相对于转动叉的角速度
vi——各个支链上主动副R所在轴线的单位矢量
结合式(1)～(3)和机构特点可求解得到各个主动臂转角、角速度、角加速度表达式为
(4)
(5)
(6)
其中
Bi=-2Limixcos(θ+γi)+2Limiysin(θ+γi)
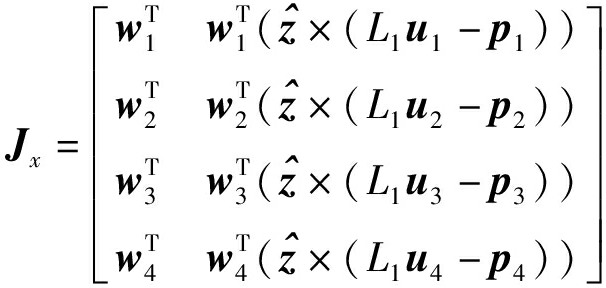
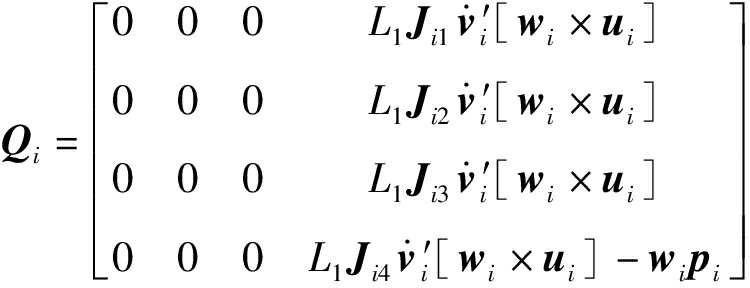
式中 J——雅可比矩阵,表征机构末端速度与主动关节速度之间的映射关系
Ji——J第i行行矢量
Jq、Jx——直接和间接雅可比矩阵
3-4-5次多项式加速度a345和梯形加速度aMT函数可分别表示为
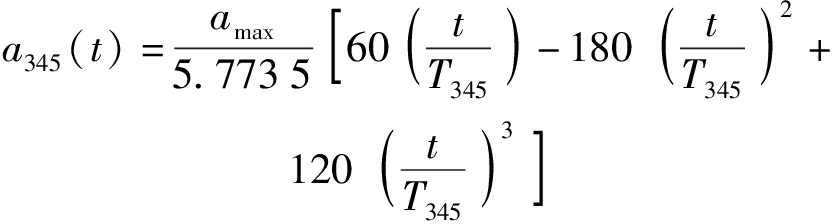
(7)
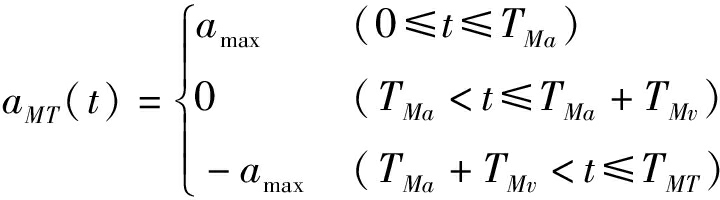
(8)
式中 amax——额定加速度
T345——3-4-5运动规律周期
TMa、TMv、TMT——梯形运动规律、匀加速阶段、匀速阶段单个周期运动时长
假设运动路径总长度为L,则3-4-5多项式和梯形运动规律的运动周期分别为
(9)
(10)
由式(7)～(10)可知,3-4-5次多项式运动规律加速度变化平稳,具有运动平稳的特征,但运动周期比梯形运动规律长,而梯形运动规律虽然运动时间短,但存在加速度突变,运动平稳性较差,为优化得到兼顾运动效率和运动平稳性的运动规律,将3-4-5多项式和梯形两种运动规律进行融合,构造345-修正梯形运动规律。
图3为融合后速度运动曲线。在此,0～t1采用345运动规律,且在t1时刻加速度达到最大值amax,t1～t2采用梯形运动规律,为匀加速运动阶段,t2～t3采用345运动规律,为变加速运动阶段,其加速度由最大值逐渐减小至0,且在t3时刻速度达到最大值,t3～t4为匀速运动阶段,保持最大速度运行,t4～t5阶段采用345运动规律,为变加速运动阶段,其加速度由0逐渐减小至负向最大,t5～t6采用梯形运动规律,为匀减速运动阶段,t6～TM采用345运动规律,为变加速运动阶段,其加速度由负向最大逐渐增加至0。为描述方便,引入系数λ1、λ2,其中λ1为图3中红色左斜线所在的6块面积组成的3-4-5次多项式运动规律区域所走路程占总路程的比例系数,λ2为图中蓝色斜方格所在加速度不变区域所走路程占总路程的比例系数。
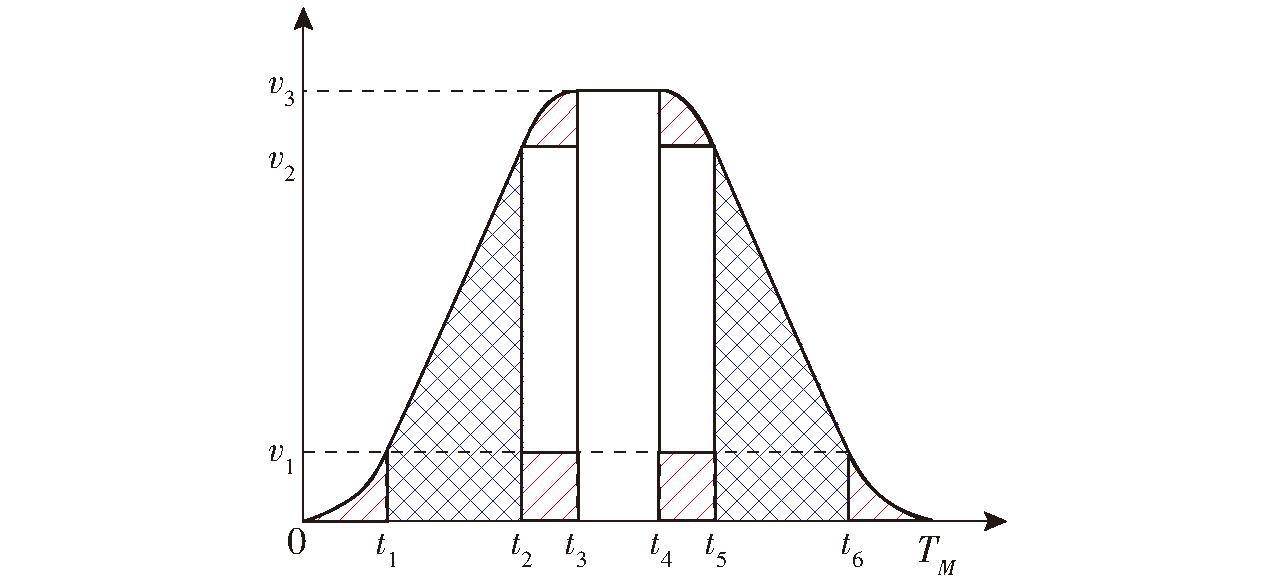
图3 345-修正梯形运动规律速度函数图
Fig.3 345-corrected trapezoidal velocity law
令总路程为L,加速度峰值为amax,根据上述构造方法,可得
v2=v1+amax(t2-t1)
t3=TM345/2+t2-t1
v3=amaxvM345_maxTM345+amax(t2-t1)
vM345_max=0.324 8amaxTM345
t4=s34/[vM345_max+amax(t2-t1)]+t3
s34=L(1-λ1-λ2)-2amax(t2-t1)(t3-t2)
t5=t4+t3-t2
t6=t5+t2-t1
s34/[vM345_max+amax(t2-t1)]
(11)
式中 TM——345-修正梯形运动规律总的运行周期
TM345——345-修正梯形运动规律中345运动规律部分所占时间
可构造出345-修正梯形运动规律的加速度函数为
aM(t)=
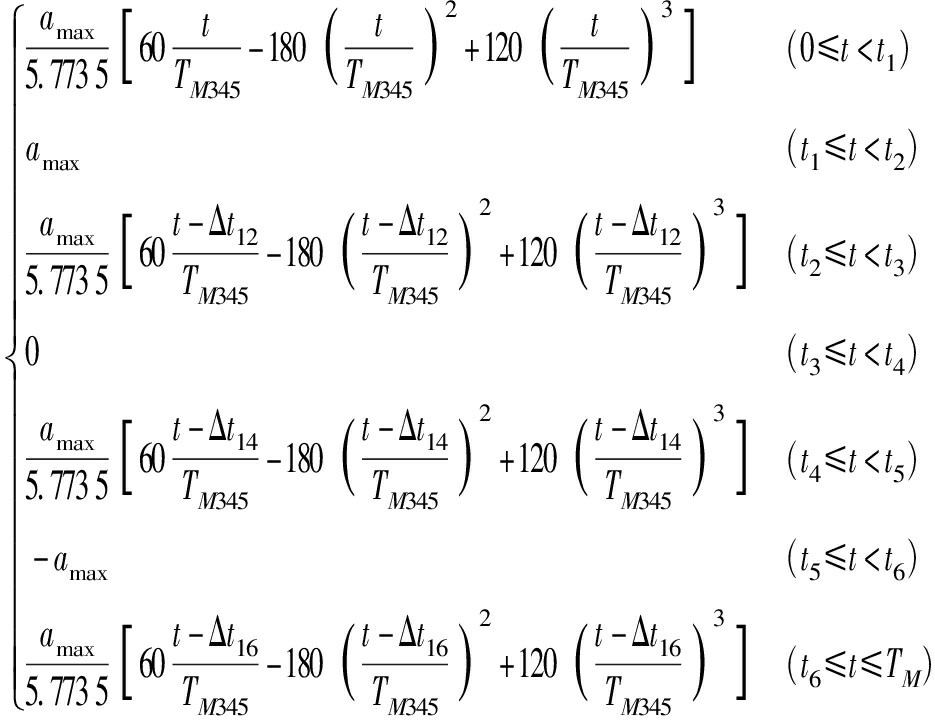
(12)
其中
Δt12=t2-t1
Δt14=t2-t1+t4-t3
Δt16=t2-t1+t4-t3+t6-t5
由于总路程为L,故由图3可得
L=λ1L+2srect+λ2L+v3(t4-t3)
(13)
其中
srect=amax(t2-t1)(t3-t2)
值得指出,若仅有加速度和路程限制,没有速度峰值限制,则当t4-t3=0时总运行时间最短,即运动规律中不存在匀速运动阶段,此时有
λ1L+2srect+λ2L=L (0≤λ1≤1;0≤λ2≤1)
(14)
可得
(15)
由此可见,此时λ1和λ2仅有一个独立变量,不失一般性,在此不妨以λ1为独立变量。将345-修正梯形运动规律应用于
机构,并设定末端加速度峰值为25 m/s2,水平距离分别为0.3、0.1、0.025 m,λ2满足关系式(15)右边界条件。图4为机构总运行时间和主动臂角加速度峰值随λ1的变化曲线。
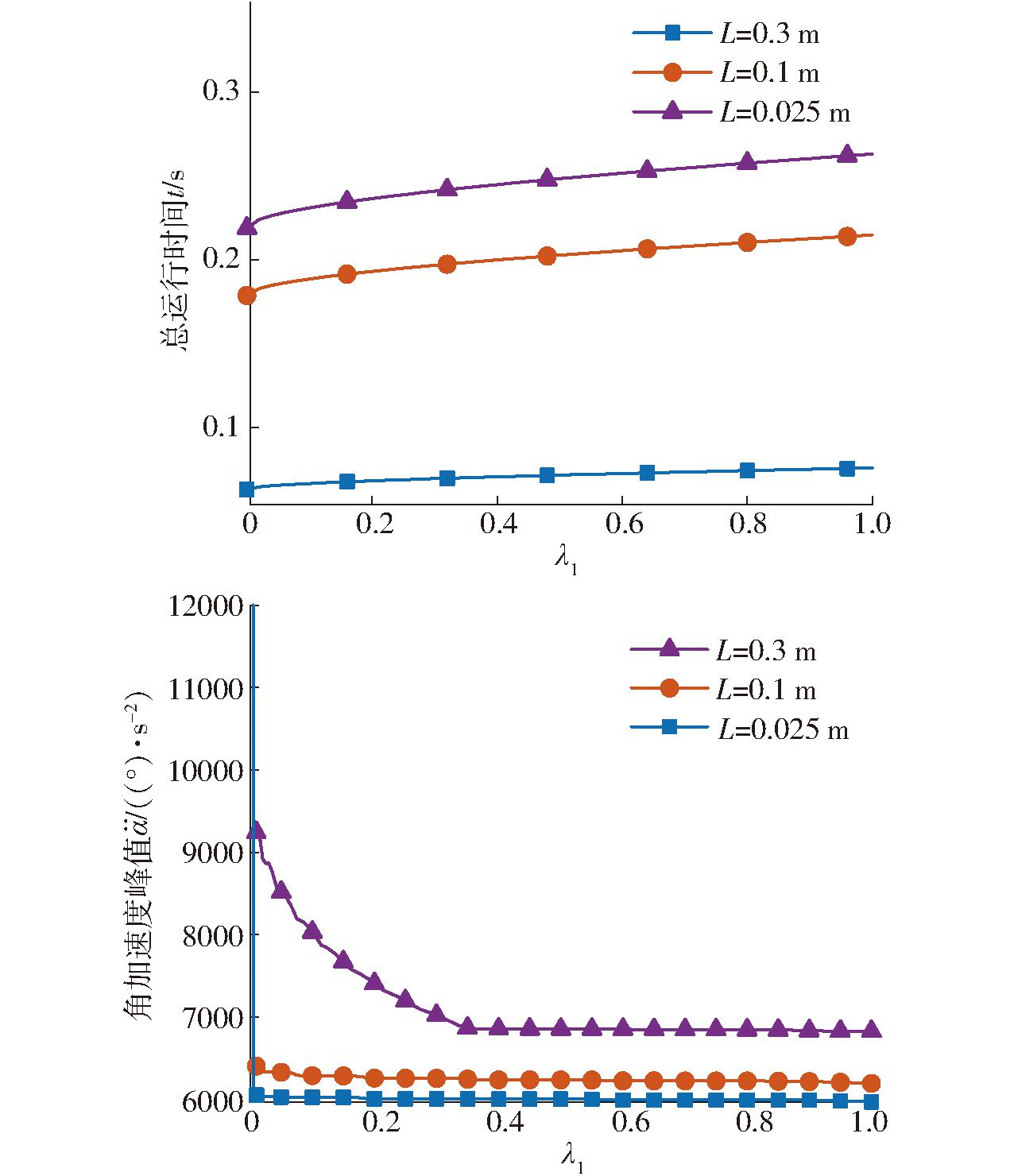
图4 总运行时间和角加速度峰值随参数λ1的变化曲线
Fig.4 Relationship between total time,peak value of angular acceleration and λ1
由图4可知,当λ1从0到1逐步增大的过程中,总运行时间逐渐增大,而主动臂角加速度峰值随之减小,这意味着并联机器人在运动过程中更加稳定,受到的冲击更小;其中,当λ1=0时,总运行时间最短,3个运动距离的运行时间分别为0.219 1、0.178 9、0.063 2 s。
为避免过大的冲击和保持末端平稳性,以及参照文献[20]中实践证明当过渡运动函数所运行时间占总运行时间一半时机构综合性能最佳,通过将TM=2TM345代入式(11),结合式(15),可解得λ1=0.2、λ2=0.46,代入以上参数后345-修正梯形运动规律总时间以及加速度运动函数可简化为
(16)
表1为在相同总位移和加速度峰值条件下,3种运动规律总运行时间和角加速度峰值的对比情况。由表1可以发现,345-修正梯形运动规律相较于3-4-5次多项式和修正梯形运动规律,总运行时间分别减少28.9%和22.9%,表明在相同的时间内,可以提升抓放频次,对生产效率有显著提升作用,而主动臂角加速度峰值与3-4-5次多项式相比略大,比修正梯形规划略小,对主动臂冲击较小。
表1 运动仿真结果
Tab.1 Simulation results of different motion laws
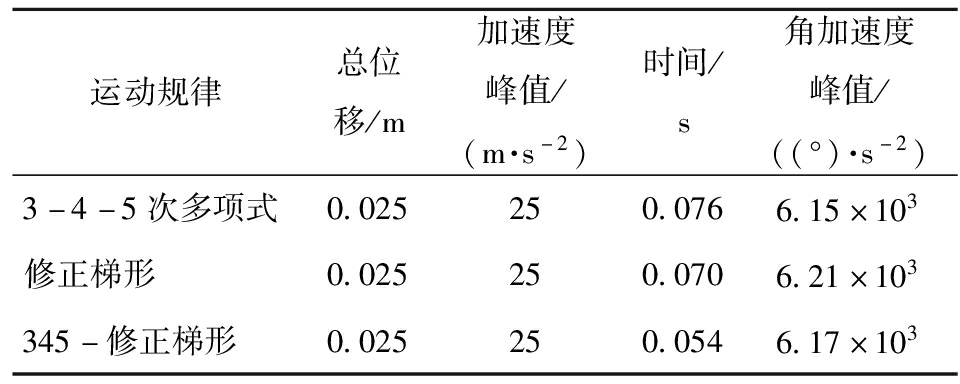
运动规律总位移/m加速度峰值/(m·s-2)时间/s角加速度峰值/((°)·s-2)3-4-5次多项式0.025250.0766.15×103修正梯形0.025250.0706.21×103345-修正梯形0.025250.0546.17×103
高速并联机器人因无累积误差,刚度大,适用于自动化生产线中物料分拣。在实际分拣工况中仅需考虑始末两端点是否可达,以及需要规划避障距离。其典型的轨迹为Adept门形轨迹,由一段水平直线和两段垂直直线组成,如图5所示。
图5 Adept 门形轨迹
Fig.5 Adept door-shaped path
加速度函数可表示为
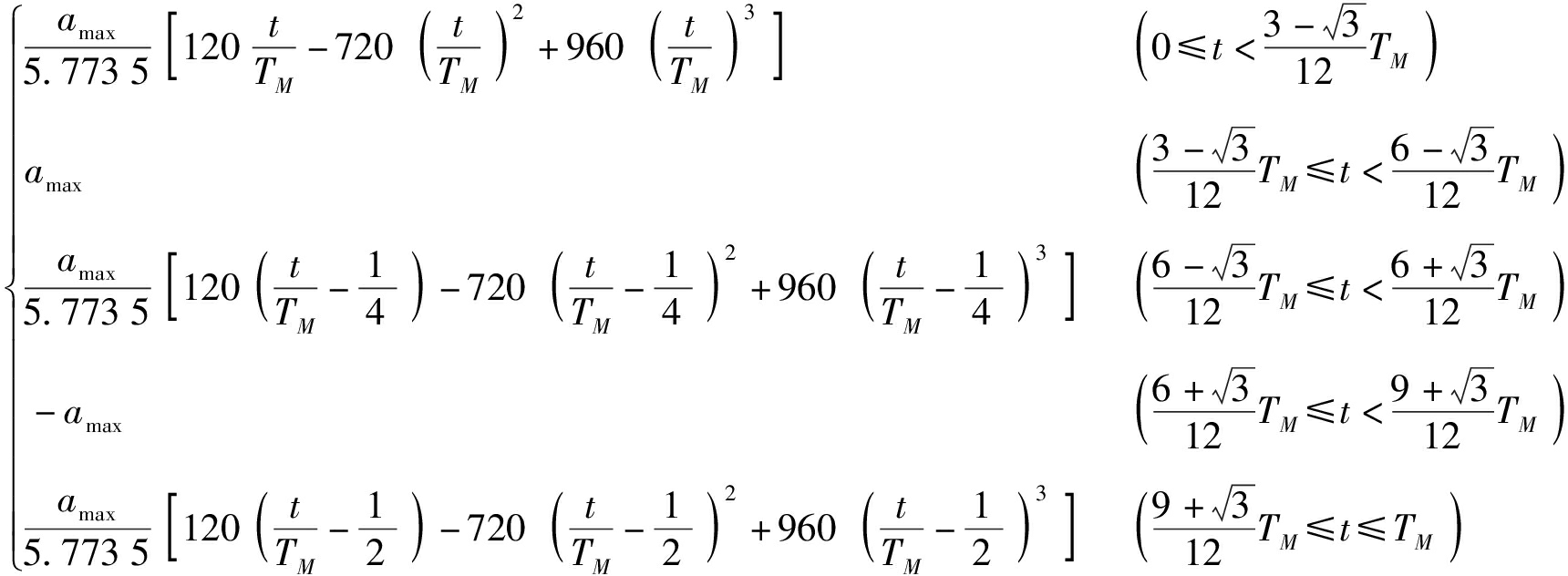
(17)
通常利用标准周期来衡量机器人拾取和放置速度,标准周期是机器人走完一条25 mm×300 mm×25 mm的路径所需的时间。它提供了一个基准,可以用来比较工业机器人速度。
在加速度峰值为25 m/s2,以345-修正梯形运动规律行走一个Adept门形轨迹过程中,主动臂角度、角速度、角加速度变化情况如图6所示。
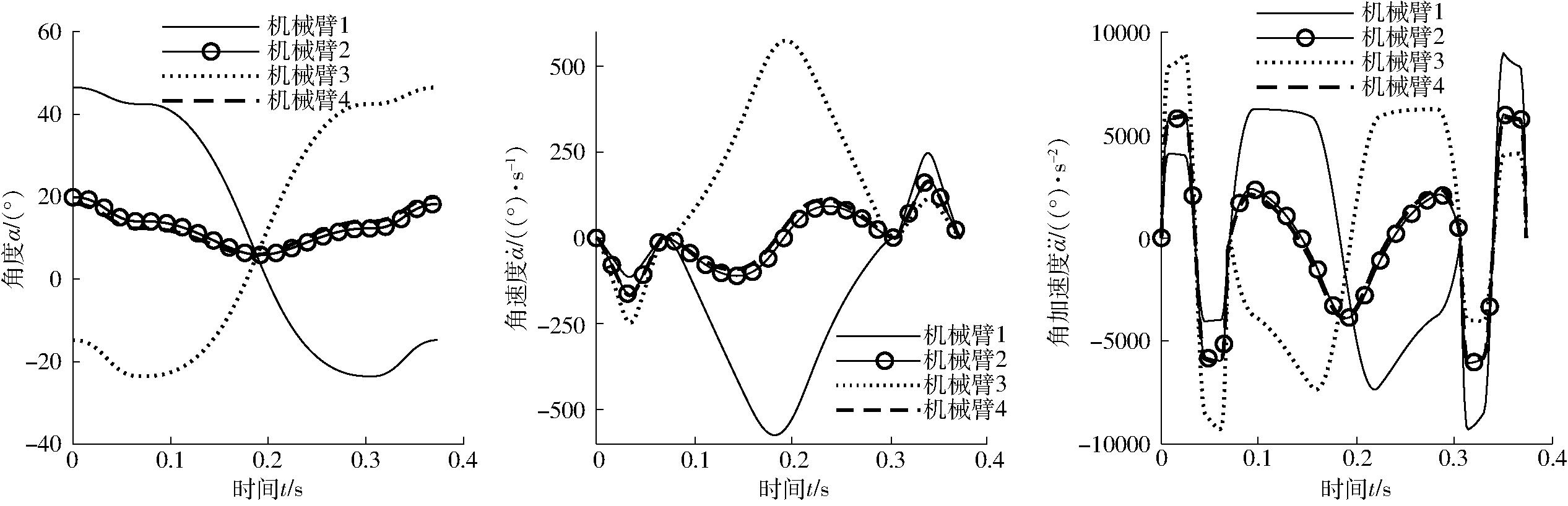
图6 Adept门形路径主动臂角度、角速度和角加速度的变化情况
Fig.6 Changes in angle,angular velocity,and angular acceleration of driving arm in Adept gate path
由图6可知,在两两直角的转弯处,容易产生角速度和角加速度的突变,进而容易造成末端执行器的抖动,对机器人末端的精度会产生较大影响,所以有必要对此加以改进。在此提出通过插补叠加过渡直角的轨迹方法。叠加过程主要分为以下步骤:
(1)确定图5中
段位移运动规律和运行时间。利用345-修正梯形运动函数,分别规划图7中
段位移的运动函数L1(t)、L2(t)、L3(t),并计算出各段位移所需运行时间T1、T2、T3。
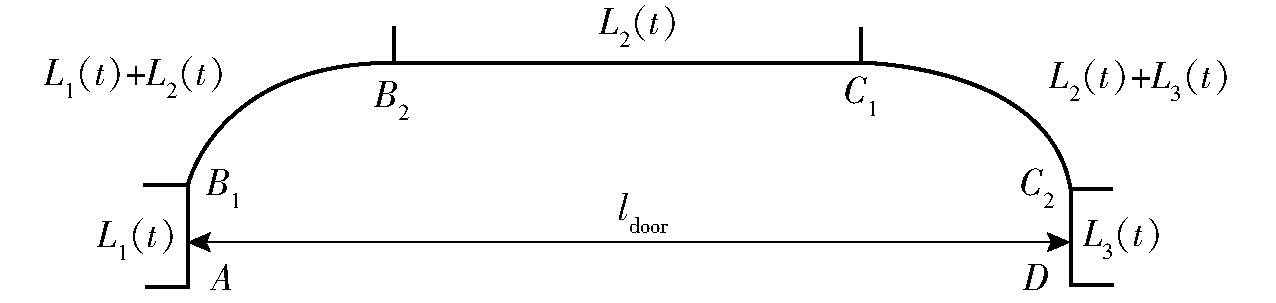
图7 插补叠加运动轨迹
Fig.7 Interpolated superimposed motion trajectory
(2)规划3段位移运动开始的时间。若等待前一段位移结束后再开始第2段位移,总时间需要T1+T2+T3,将导致运行时间过长,若前1段位移还未结束就开始后一段位移,明显可以提升运行效率,但这将导致加速度变大,影响机构平稳性,故后一段位移开始时间应选择恰当时机。如图5所示,设第1段竖直段L1(t)从0时刻开始运行,并令第2段水平段开始的时间为T1kmix,则根据对称原则,第3段竖直段开始时间为T2-T1(1-2kmix),最终总运行时间可表示为T2+2kmixT1,其中kmix为插补叠加比例系数,运行轨迹如图7所示。
此外,若第2段路径太短,为避免第1、3段同时运动的问题,需满足
T2-T1(1-2kmix)≥T1
(18)
进而可得
(19)
则总路径规划为
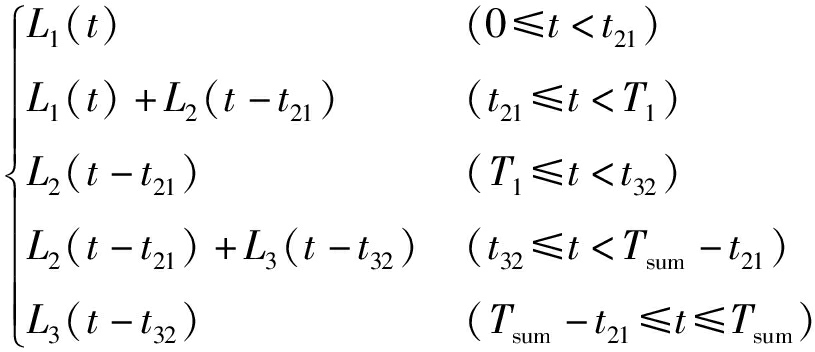
(20)
其中
t21=T1kmix t32=T2-T1(1-2kmix)
Tsum=T2+2T1kmix
式中 t21、t32——第2段和第3段运动开始的时刻
Tsum——总运行时间
在额定加速度限制下,若两直线段叠加的时间越早(即叠加比例系数kmix越小),则总运行时间越短,但相对的叠加时间过早,将导致瞬时向心加速度过大,容易导致末端执行器不稳定。为此,在考虑最大角加速度峰值和总运行时间的前提下,对于选取最佳叠加比例系数提出以下搜索方法:令kmix的初始值为
最大角速度峰值
为kmix,1所对应各个主动臂中最大角速度峰值,并以步长Δk逐渐增大kmix,直至kmix=1,令kmix,i=kmix,i-1+(i-1)Δk,并依据式(6)、(16)计算kmix,i所对应的总运行时间ti和各个主动臂中最大角加速度峰值
为计算最优kmix的综合评价指标,使用熵权法[21]来确定最大角速度峰值和总运行时间的权重,熵权法计算流程为:
(1)对数据归一化处理
(21)
(22)
(2)计算各个指标熵权
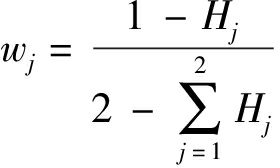
(23)
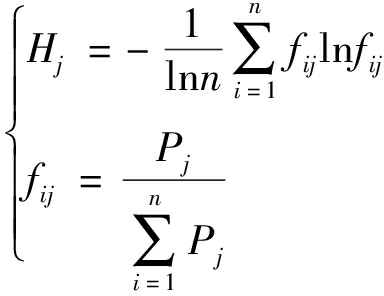
(24)
其中
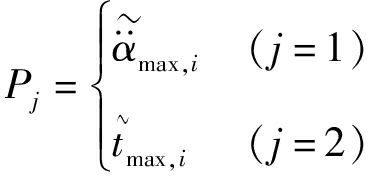
式中 Hj——第j个指标熵值
wj——第j个指标熵权
(3)计算各项综合评价指标
(25)
式中 Mi——第i项的综合评价指标
在得到各项kmix,i所对应的综合评价指标之后,选取其中最小综合评价指标所对应的kmix,i作为叠加比例系数,整体流程如图8所示。
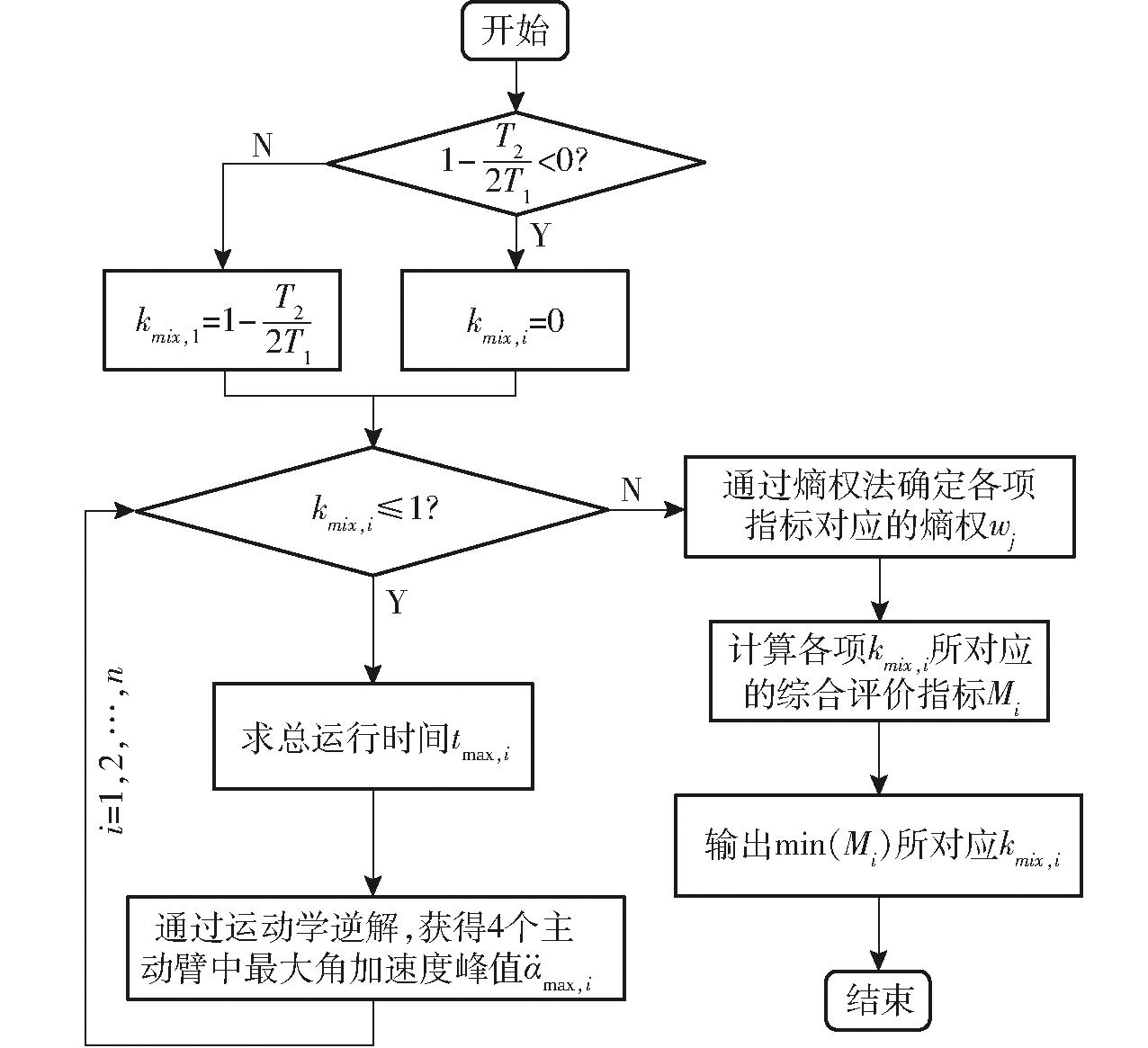
图8 求取叠加比例系数的模块流程图
Fig.8 Flowchart of superposition scale coefficient module
以加速度峰值amax为25 m/s2、水平运动距离0.3 m、越障高度0.025 m的门形轨迹为例,并采用345-修正梯形运动规律,说明kmix选取方法,令Δk=0.01,图9为综合评价指标随kmix的变化曲线,当kmix=0.73时综合评价指标最小,因此插补叠加比例系数为0.73。
图9 综合评价指标随kmix变化曲线
Fig.9 Change curve of comprehensive evaluation index with kmix
当叠加比例系数kmix=0.73时,主动臂角度、角速度、角加速度随时间的变化曲线如图10所示。在相同总位移和加速度峰值条件下,插补叠加轨迹和Adept门形轨迹的总运行时间,角加速度峰值和峰值转矩对比情况如表2所示。由表2可知,采用优化后的轨迹与传统的Adept门形轨迹相比,不仅在轨迹拐角处更加顺滑(图5和图7),总的运行时间更短;其中,角加速度峰值比传统门形轨迹减少3.6%,单次消耗时间从0.377 s减至0.336 s,减少10.9%,峰值转矩相近。
表2 插补叠加轨迹与Adept门形轨迹仿真结果
Tab.2 Simulation results of three-stage fusion path and Adept gate path
运动轨迹总位移/m加速度峰值/(m·s-2)总运行时间/s角加速度峰值/((°)·s-2)峰值转矩/(N·m)插补叠加轨迹0.025250.3368.96×1030.065Adept门形轨迹0.025250.3779.29×1030.062
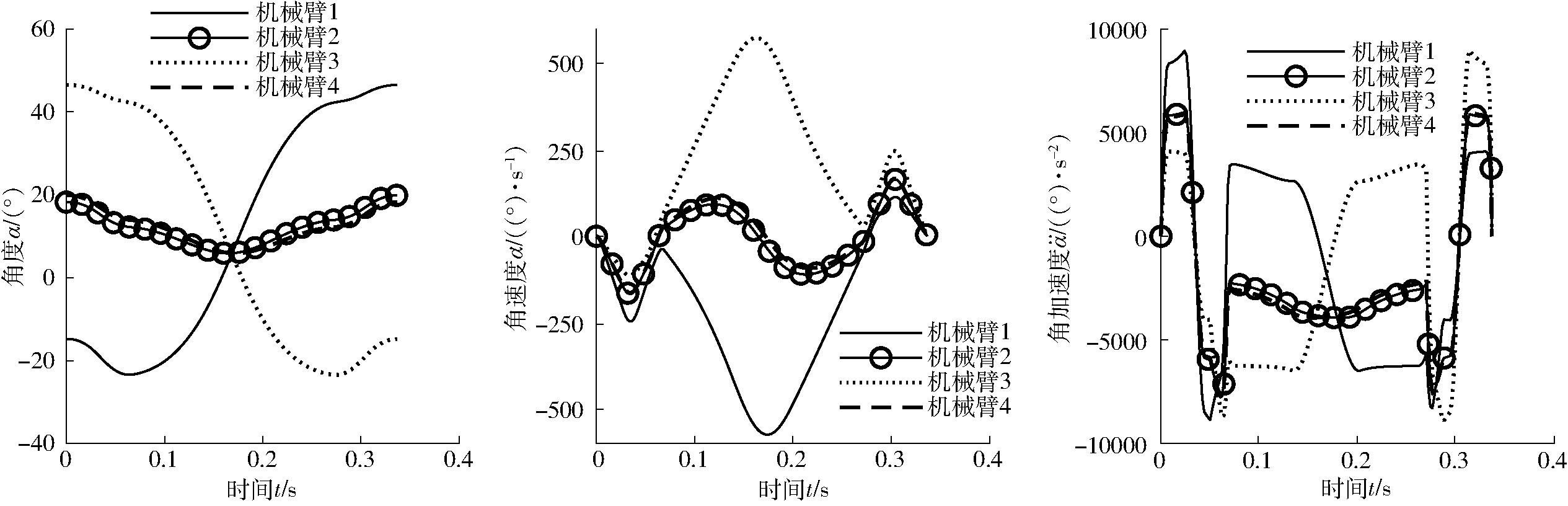
图10 插补叠加轨迹主动臂角度、角速度和角加速度的变化曲线
Fig.10 Changes in angle,angular velocity and angular acceleration of driving arm in interpolated superimposed motion trajectory
在目标位置信息已知的基础上,计算运行轨迹中各个位置所对应的每个轴的进给指令,然后传达给各个电机轴以使机器人参考点达到指定位置。
插补叠加轨迹插补流程如图11所示。输入始末位置、越障高度和加速度峰值;依据始末两点的位置,将总的路径分解成上升、水平、下降3段,通过叠加比例系数模块选择kmix;依据kmix和运行时刻t(i)计算各个坐标轴上的分量,再依次运行轨迹插补叠加模块和位置逆解模块最终输出各个主动臂角度。
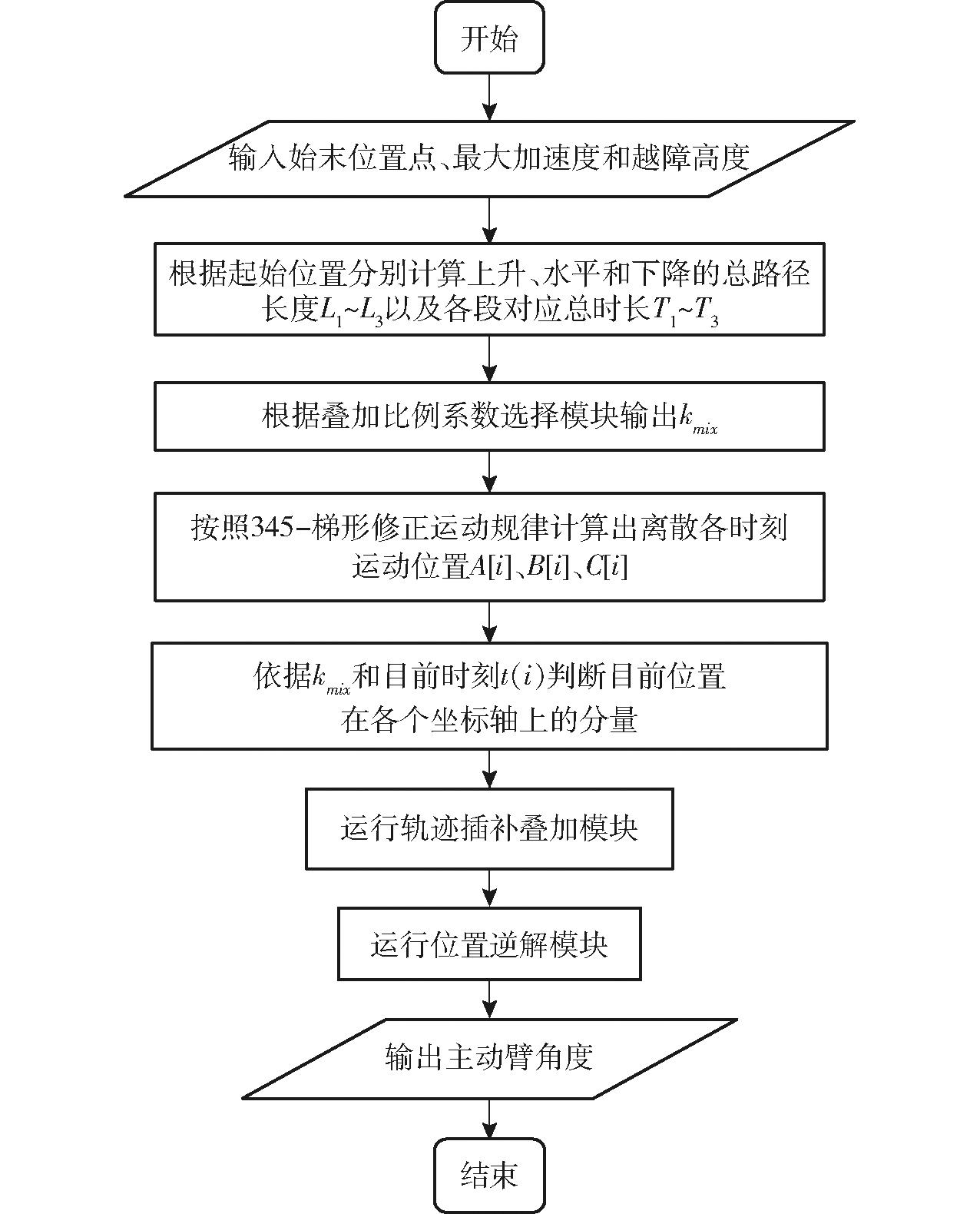
图11 路径插补整体流程图
Fig.11 Flowchart of path interpolation program
采用前文所提出的345-修正梯形运动规律,结合融合比例系数选择模块所确定的kmix生成插补叠加过渡直角的轨迹,并依照运动规律将整条轨迹路径按提前设置好的时间间隔生成插补点位置。轨迹插补叠加模块流程如图12所示。
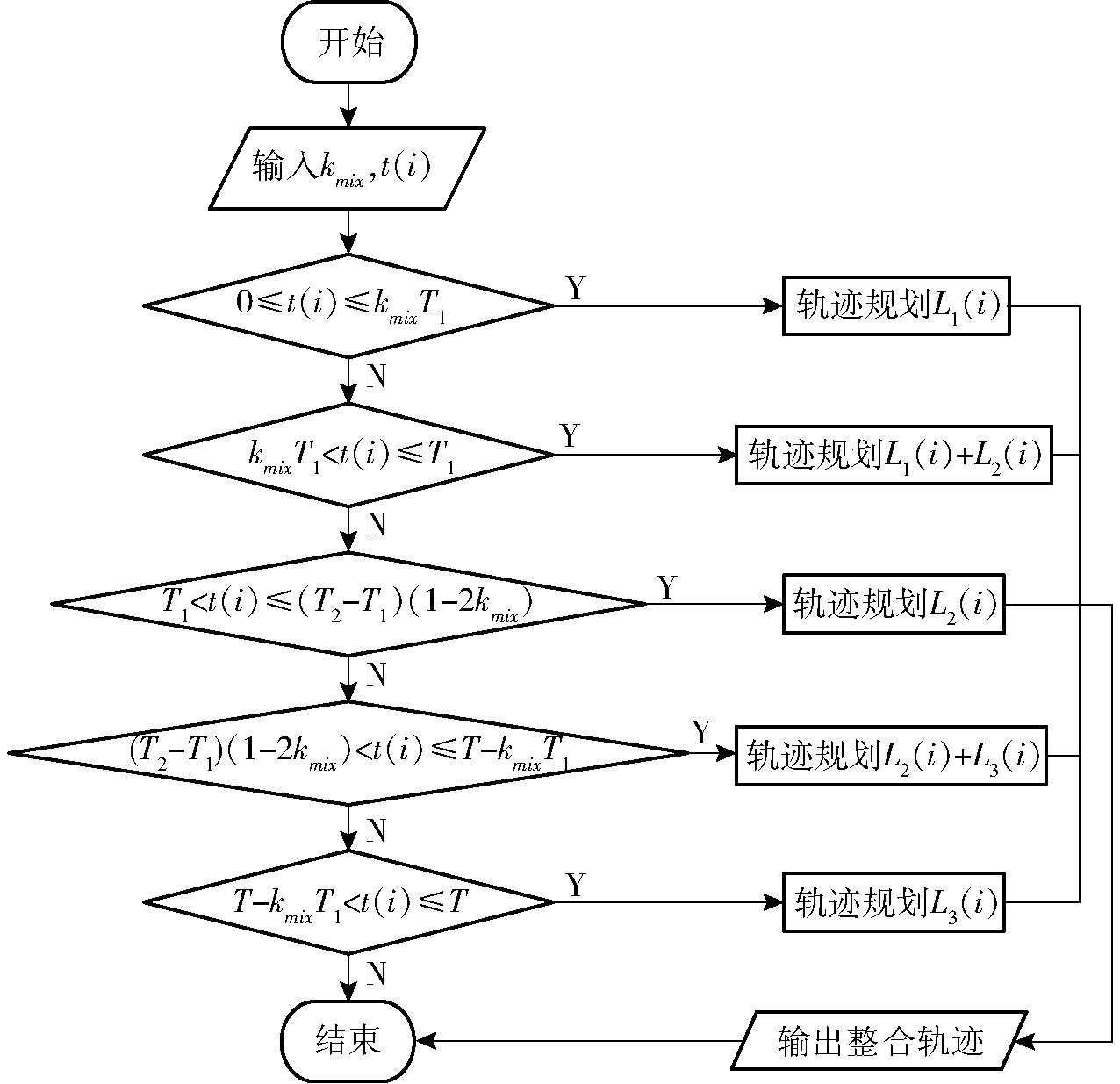
图12 插补叠加模块流程图
Fig.12 Flowchart of interpolation and superposition module
选取两个具有代表性的运动方向0°和90°,并使机器人在两个方向上以不同加速度峰值沿插补叠加路径运行,同时记录运行时电机位置误差(PE)、指令转速(PTPVCMD)和实际电流(IQ),来反映机构性能。末端加速度峰值从5 m/s2开始,以5 m/s2逐步递增,通过记录机器人样机每分钟在插补叠加门形路径上运行的运动频次进而评估其性能,图13为试验样机在两个运动方向0°和90°上样机运动实物图。
图13 试验样机
Fig.13 Experimental prototype
同一样机在不同运动方向和加速度峰值的情况下,采用3-4-5运动规律和345-修正梯形运动规律的周期、运动频次、最大位置误差和最大实际电流对比如表3所示。由表3可以发现,随着加速度峰值的提高,抓放频次、最大位置误差、最大实际电流都逐渐变大,当加速度峰值达到25 m/s2时,抓放频次达到最大,在此基础上再提升加速度峰值,会由于最大位置误差(PE)超过额定最大误差范围而报错。因为本并联机器人末端动平台存在一个结构角,所以从动臂沿着90°方向运动的夹角相对于0°方向运动的夹角更小,这意味着所需克服的力矩更小,抓放频次更高。
表3 样机运动性能试验结果
Tab.3 Prototype motion performance test
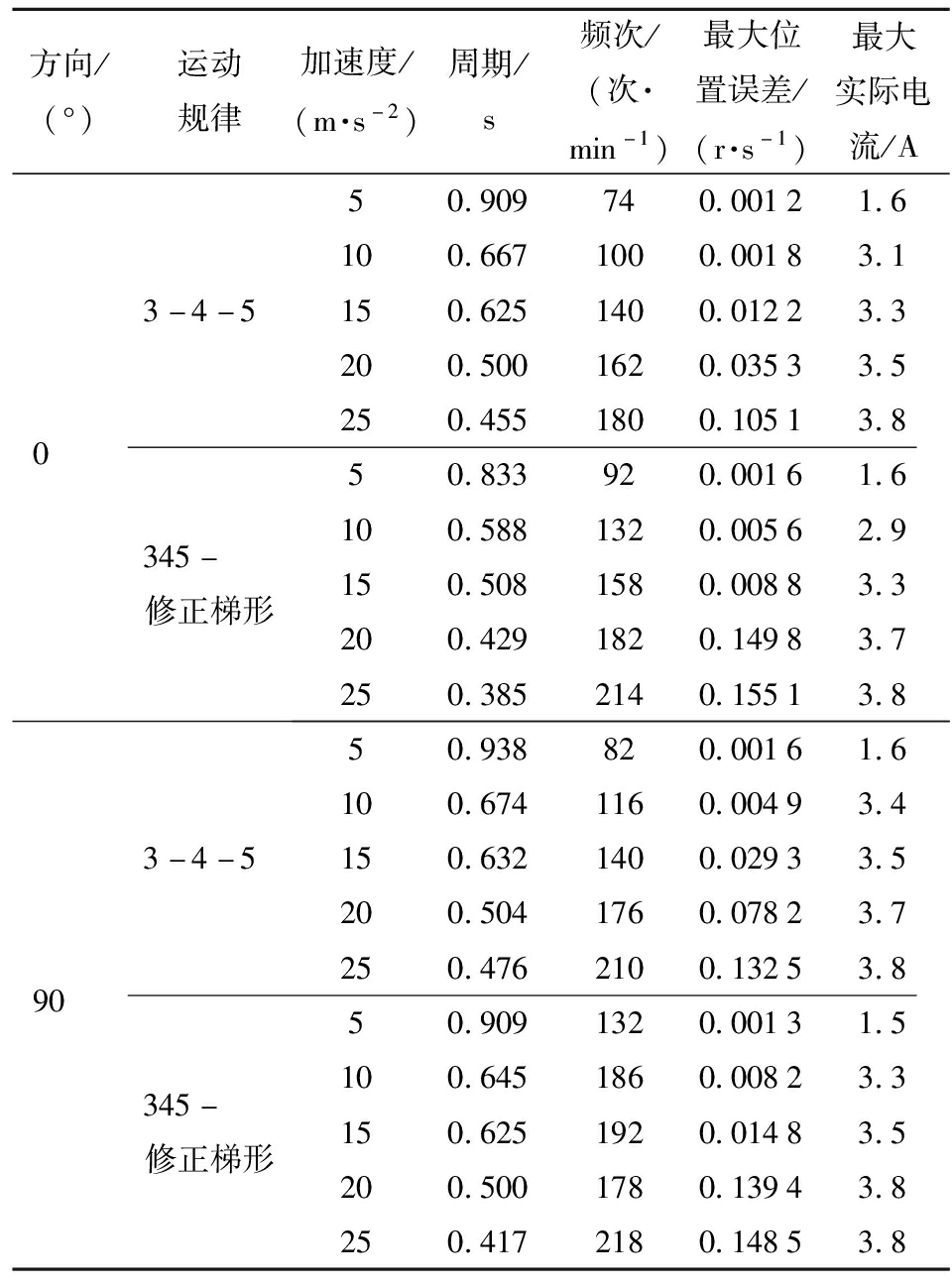
方向/(°)运动规律加速度/(m·s-2)周期/s频次/(次·min-1)最大位置误差/(r·s-1)最大实际电流/A03-4-550.909740.00121.6100.6671000.00183.1150.6251400.01223.3200.5001620.03533.5250.4551800.10513.8345-修正梯形50.833920.00161.6100.5881320.00562.9150.5081580.00883.3200.4291820.14983.7250.3852140.15513.8903-4-550.938820.00161.6100.6741160.00493.4150.6321400.02933.5200.5041760.07823.7250.4762100.13253.8345-修正梯形50.9091320.00131.5100.6451860.00823.3150.6251920.01483.5200.5001780.13943.8250.4172180.14853.8
由表3可知,样机采用本文提出的345-修正梯形运动规律和插补叠加轨迹之后,相较于传统Adept门形轨迹规划[22]、圆弧过渡轨迹规划方法[23-24]、Lamé轨迹规划方法[25-26]工作效率分别提升55.7%、36.3%、1.8%。
(1)提出了一种采用单动平台结构的新型四自由度高速并联机构,与采用双平台的并联机器人相比,末端质量更轻,具有良好加减速性能。
(2)提出一种融合了3-4-5次多项式和修正梯形运动规律的新运动函数,相较于3-4-5次多项式运动规律和修正梯形运动规律,运行时间分别减少28.9%和22.9%,运行效率有显著提高。
(3)提出一种插补叠加轨迹规划方法,并基于总运行时间最短和主动臂角加速度峰值最小优选插补叠加比例系数kmix,可实现高速且平稳的运动。
(4)样机试验结果表明,运动频次可高达218次/min,验证了本文所提出的运动规律函数以及轨迹规划方法的优越性。
[1] 刘辛军,汪劲松,高峰,等.并联机器人机构新构型设计的探讨[J].中国机械工程,2001,12(12):1339-1342.
LIU Xinjun,WANG Jinsong,GAO Feng,et al.Discussion on new configuration design of parallel robot mechanism[J].China Mechanical Engineering,2001,12(12):1339-1342.(in Chinese)
[2] PIERROT F,COMPANY O.H4:a new family of 4-dof parallel robots[C]∥Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics.IEEE,1999:508-513.
[3] KRUT S,COMPANY O,BENOIT M,et al.I4:a new parallel mechanism for SCARA motions[C]∥Proceedings of the IEEE International Conference on Robotics and Automation.IEEE,2003:1875-1880.
[4] KRUT S,COMPANY O,NABAT V,et al.Heli4:a parallel robot for SCARA motions with a very compact traveling plate and a symmetrical design[C]∥Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems.IEEE,2006:1656-1661.
[5] NABAT V,COMPANY O,KRUT S,et al.Par4:very high speed parallel robot for pick-and-place[C]∥Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems.IEEE,2005:1202-1207.
[6] 杨化林,钟岩,姜沅政,等.基于时间与急动度最优的并联式采茶机器人轨迹规划混合策略[J].机械工程学报,2022,58(9):62-70.
YANG Hualin,ZHONG Yan,JIANG Yuanzheng,et al.Hybrid trajectory planning hybrid strategy for parallel tea picking robot based on optimal time and urgency[J].Journal of Mechanical Engineering,2022,58(9):62-70.(in Chinese)
[7] WU P,WANG Z,JING H,et al.Optimal time-Jerk trajectory planning for Delta parallel robot based on improved butterfly optimization algorithm[J].Applied Sciences,2022,12(16):8145.
[8] BADRIKOUHI M,BAMDAD M.Smooth trajectory planning based on direct collocation method for cable-driven parallel robots with central spine[J].Mech.Solids,2022,57:652-670.
[9] LOUIS-THOMAS S,CLÉMENT G.Kinematically redundant planar parallel mechanisms:kinematics,workspace and trajectory planning[J].Mechanism and Machine Theory,2018,119:91-105.
[10] 梅江平,臧家炜,乔正宇,等.三自由度Delta并联机械手轨迹规划方法[J].机械工程学报,2016,52(19):9-17.
MEI Jiangping,ZANG Jiawei,QIAO Zhengyu,et al.Three-degree-of-freedom Delta parallel manipulator trajectory planning method[J].Journal of Mechanical Engineering,2016,52(19):9-17.(in Chinese)
[11] 胡建平,靳合琦,常燕超,等.基于Delta并联机构钵苗移栽机器人尺度综合与轨迹规划[J].农业机械学报,2017,48(5):28-35.
HU Jianping,JIN Heqi,CHANG Yanchao,et al.Scale synthesis and trajectory planning of bowl seedling transplanting robot based on Delta parallel mechanism[J].Transactions of the Chinese Society for Agricultural Machinery,2017,48(5):28-35.(in Chinese)
[12] NAN W,TANG X,SONG B.A new automatic motion planning algorithm for a 4-degree-of-freedom parallel kinematic manipulator based on the centre sphere method[J].Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture,2015,229(Supp.l):64-77.
[13] LI G,WANG Y.Industrial robot optimal time trajectory planning based on genetic algorithm[C]∥2019 IEEE International Conference on Mechatronics and Automation (ICMA),2019:136-140.
[14] CONEJO-BENITEZ C R,TORRES I,ROCHA-C
ZATL E,et al.Third order super twisting algorithm applied to a robotic arm with 3 degrees of freedom[C]∥2021 IEEE 5th Colombian Conference on Automatic Control(CCAC),2021:80-85.
[15] CHEN Z,XU S,WU J,GENG Y.The simulation study of optimization of pick-and-place route for Delta robot based on lame curves[C]∥2018 Chinese Control and Decision Conference (CCDC),2018:467-471.
[16] CHEN D,LI S,WANG J,et al.A multi-objective trajectory planning scheme for parallel assembly mechanism with B-spline curves[C]∥2018 IEEE 15th International Conference on Networking,Sensing and Control (ICNSC),2018:1-6.
[17] 韩艳东.面向高速搬运的Delta机器人轨迹优化及控制[D].哈尔滨:哈尔滨工业大学,2017.
HAN Yandong.Delta robot trajectory optimization and control for high-speed handling[D].Harbin:Harbin Institute of Technology,2017.(in Chinese)
[18] GUO J,ZHANG Y,SHI J.Trajectory planning of 3-TPT parallel robot based on PH curve[C]∥2022 14th International Conference on Measuring Technology and Mechatronics Automation (ICMTMA),2022:269-272.
[19] 汪满新,黄田,冯虎田,等.一种三平一转四自由度并联机构:ZL201510786414.6[P].2015-11-16.
[20] 彭国勋,肖正扬.自动机械的凸轮机构设计[M].北京:机械工业出版社,1990:36-41.
[21] LI Z,LUO Z,WANG Y,et al.Suitability evaluation system for the shallow geothermal energy implementat-ion in region by entropy weight method and TOPSIS method[J].Renewable Energy,2022,184:564-576.
[22] 宋远璞.四自由度高速并联机器人机构动力学分析与运动控制研究[D].南京:南京理工大学,2018.
SONG Yuanpu.Research on dynamic analysis and motion control of four-degree-of-freedom high-speed parallel robot mechanism[D].Nanjing:Nanjing University of Science and Technology,2018.(in Chinese)
[23] 梁旭,苏婷婷,贾智琪,等.并联Delta机器人及其轨迹规划方法综述[J].科学技术与工程,2022,22(11):4271-4279.
LIANG Xu,SU Tingting,JIA Zhiqi,et al.Overview of parallel Delta robots and their trajectory planning methods[J].Science Technology and Engineering,2022,22(11):4271-4279.(in Chinese)
[24] 邓泽晓.并联机器人机构学分析及轨迹规划方法研究[D].哈尔滨:哈尔滨工程大学,2020.
DENG Zexiao.Research on mechanism analysis and trajectory planning methods for parallel robots[D].Harbin:Harbin Engineering University,2020.(in Chinese)
[25] ZHANG H P,WANG M X,LAI H B,et al.Trajectory planning of a 4-RR(SS)2 high-speed parallel robot[J].Robotica,2022,40(8):2666-2682.
[26] 张惠普.四自由度高速并联机器人动力尺度综合及运动控制研究[D].南京:南京理工大学,2021.
ZHANG Huipu.Research on dynamic scale synthesis and motion control of four degrees of freedom high speed parallel robot[D].Nanjing:Nanjing University of Science and Technology,2021.(in Chinese)